이진탐색
오늘은 이진 탐색에 대해 정리해보려 한다.
영어로는 Binary Search라고 한다.
이진 탐색은 정렬되어 있는 숫자들 중에서 특정 숫자를 찾는다.
-값들 중에 절반을 기준으로 원하는 값을 찾는다.
-절반을 나눈 값을 기준으로 원하는 값이 있는 쪽에서 다시 절반을 나눈다.
즉 이진 탐색은 숫자를 절반씩 지워나가면서 찾는다.
따라서 시간 복잡도는 O(log n)이 된다.
여기서 의문점이 들 수 있다.
정렬해야 하면 O(log n)이 아니라 결국 O(n log n) 아닌가요? -> yes
따라서 이미 배열이 정렬되어 있다면 Binary Search가 효율적이다.
또는 숫자 찾기를 엄청 많이 해야 하는 경우에는 오히려 정렬을 한 뒤에 Binary Search를 하는 것이 좋다.
이제 이진 탐색을 구현해보자.
1. 재귀 함수를 사용하여 구현
import java.util.Scanner;
public class Main{
static int n;
static int[] arr;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n =sc.nextInt();
int q =sc.nextInt();
arr = new int[n];
for (int i=0;i<arr.length;i++){
arr[i] = sc.nextInt();
}
Check(0,n-1,q);
}
//반으로 쪼개어 탐색
static void Check(int start , int end, int s){
if (start>end){
System.out.println(-1);
return;
}
if (arr[start]==s){
System.out.println(start);
return;
} else if (arr[end]==s) {
System.out.println(end);
return;
}
int mid = (start+end)/2;
if (arr[mid]==s) {
System.out.println(mid);
return;
}
if (arr[mid]<s){
Check(mid+1,end,s);
}
else {
Check(start,mid-1,s);
}
}
}중요한 점은 재귀 함수 부분에서 시작 부분과 끝부분이 우리가 찾는 값이면 바로 그 위치를 반환하는 것이다.
만약 우리가 찾는 값이 없으면 -1을 반환하게 구현하였다.
2. 비재 귀적 구현
import java.util.Scanner;
public class Main {
static int n;
static int[] arr;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n =sc.nextInt();
int q =sc.nextInt();
arr = new int[n];
for (int i=0;i<arr.length;i++){
arr[i] = sc.nextInt();
}
Check(0,n-1,q);
}
//반으로 쪼개어 탐색
static void Check(int myStart , int myEnd, int s){
int start,end,mid;
if (arr[myStart]>s){
System.out.println(-1);
return;
} else if (arr[myStart]==s) {
System.out.println(myStart);
return;
}
if (arr[myEnd]<s){
System.out.println(-1);
return;
} else if (arr[myEnd]==s) {
System.out.println(myEnd);
return;
}
start =myStart;
end =myEnd;
while (start+1<end){
mid = (start+end)/2;
if (arr[mid] ==s){
System.out.println(mid);
return;
} else if (arr[mid]>s) end = mid;
else start=mid;
}
System.out.println(-1);
}
}재귀로 구현한 것을 단순하게 비 재귀로 표현한 것이라 동작원리는 같다.
이제 이진 탐색 알고리즘을 어디에 사용할 수 있는지 궁금할 것이다.
숫자 개수 세기

이 문제에서 이진 탐색을 사용하는 이유는 간단하다.
숫자 찾기를 엄청 많이 해야 하는 경우에는 오히려 정렬을 한 뒤에 Binary Search를 하는 것이 좋기 때문이다.
정답 코드
import java.util.Arrays;
import java.util.Scanner;
//숫자 세기
public class Main {
static int n;
static int[] arr;
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
n =sc.nextInt();
int q = sc.nextInt();
arr = new int[n];
for (int i=0;i<n;i++){
arr[i] = sc.nextInt();
}
Arrays.sort(arr);
for (int i=0;i<q;i++){
int request = sc.nextInt();
int front = frontFind(request);
int end = endFind(request);
if (front==-1) System.out.println(0);
else System.out.println(end-front+1);
}
}
static int frontFind(int result){
int start;
int end;
if (arr[0] <result) start=0;
else {
if (arr[0]>result)return -1;
else return 0;
}
if (arr[n-1]>=result)end=n-1;
else return -1;
while (start+1<end){
int mid=(start+end)/2;
if (arr[mid]<result)start = mid;
else end = mid;
}
if (arr[end]==result)return end;
else return -1;
}
static int endFind(int result){
int start;
int end;
if (arr[0]<=result)start=0;
else return -1;
if (arr[n-1]>result)end=n-1;
else {
if (arr[n-1]<result)return -1;
else return n-1;
}
while (start+1<end){
int mid=(start+end)/2;
if (arr[mid]<=result)start=mid;
else end =mid;
}
if (arr[start]==result)return start;
else return -1;
}
}
이진 탐색을 사용하기 위해 수를 정렬한다.
이후 frontFind, endFind매서드를 만들어서 처음 값이 등장한 index와 마지막에 등장하는 index를 구한다.
그 차이를 구하면 된다. 이진 탐색을 이용하면 시간 복잡도에서 엄청난 이점을 가져갈 수 있다.
나무 자르기
위 문제도 이진 탐색을 사용하여 효율적으로 풀 수 있다.
이유는 간단하다. 만약 5층까지 있다고 하자.
3층으로 나누었을 때, 가능하다면 4,5층은 시도하지 않아도 가능하다는 것을 알 수 있다.
정답 코드
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
int M = in.nextInt();
int[] tree = new int[N];
int start = 0;
int end = 0;
for(int i = 0; i < N; i++) {
tree[i] = in.nextInt();
if(end < tree[i]) {
end = tree[i];
}
}
// 이분 탐색
while(start < end) {
int mid = (start + end) / 2;
long sum = 0;
for(int treeHeight : tree) {
if(treeHeight - mid > 0) {
sum += (treeHeight - mid);
}
}
if(sum < M) {
end = mid;
}
else {
start = mid + 1;
}
}
System.out.println(start - 1);
}
}알고리즘을 살펴보면, 나무들 중에 최댓값을 구한다. -> 자를 수 있는 최대의 높이
이진 탐색을 이용하여 중간 값을 기준으로 가능 여부를 확인한다.
나무의 잘린 길이 = 나무의 높이 - 자르는 위치
잘린 나무의 길이의 합을 구하고 그 값이 우리가 원하는 값과 비교한다.
더 크다면, 높이를 높여도 된다. 개수가 부족하다면 높이를 낮추어 더 많은 나무를 잘라야 한다.
NN단표
특정 숫자가 몇 번째인가?
이 문제 또한 이진 탐색을 활용하여 풀 수 있다.
정답 코드
import java.util.Scanner;
// NN 단표
public class Main {
static long n;
static long k;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextLong();
k = sc.nextLong();
long start = 1,end=n*n+1;
while (start+1<end){
long mid = (start+end)/2;
long myOrder = getOrder(mid);
if (myOrder<=k)start=mid;
else end =mid;
}
System.out.println(start);
}
static long getOrder(long x){
long result=0;
for (int i=1;i<=n;i++){
if (i*n<x)result+=n; //맨 마지막수
else {
if (x % i == 0) result += (x / i) - 1;
else result += x / i;
}
}
return result+1;
}
}이진 탐색을 사용한 부분은 우리가 찾는 수가 시작점에 위치할 때까지 반으로 나누게 된다.
즉 해당수보다 작은 값의 개수를 찾는 것이 관건이다.
따라서 getOrder매서드가 중요해진다.
n이 4면 아래와 같다.
1 2 3 4
2 4 6 8
3 6 9 12
4 8 12 16
앞의 수만 보면 x보다 작은 수를 구할 수 있다.
만약 x가 12라 하면 앞에 1 2 3 4는 모두 작기 때문에 총 개수 4개를 더한다.
근데 만약 4번째 줄처럼 12가 포함될 경우 카운트를 하면 안 된다.
따라서 12가 4로 나누어지면 -1을 해준다.
또한 중요한 점은 수의 범위가 매우 커지기 때문에 long타입으로 설정해야 한다.
중복 없는 구간
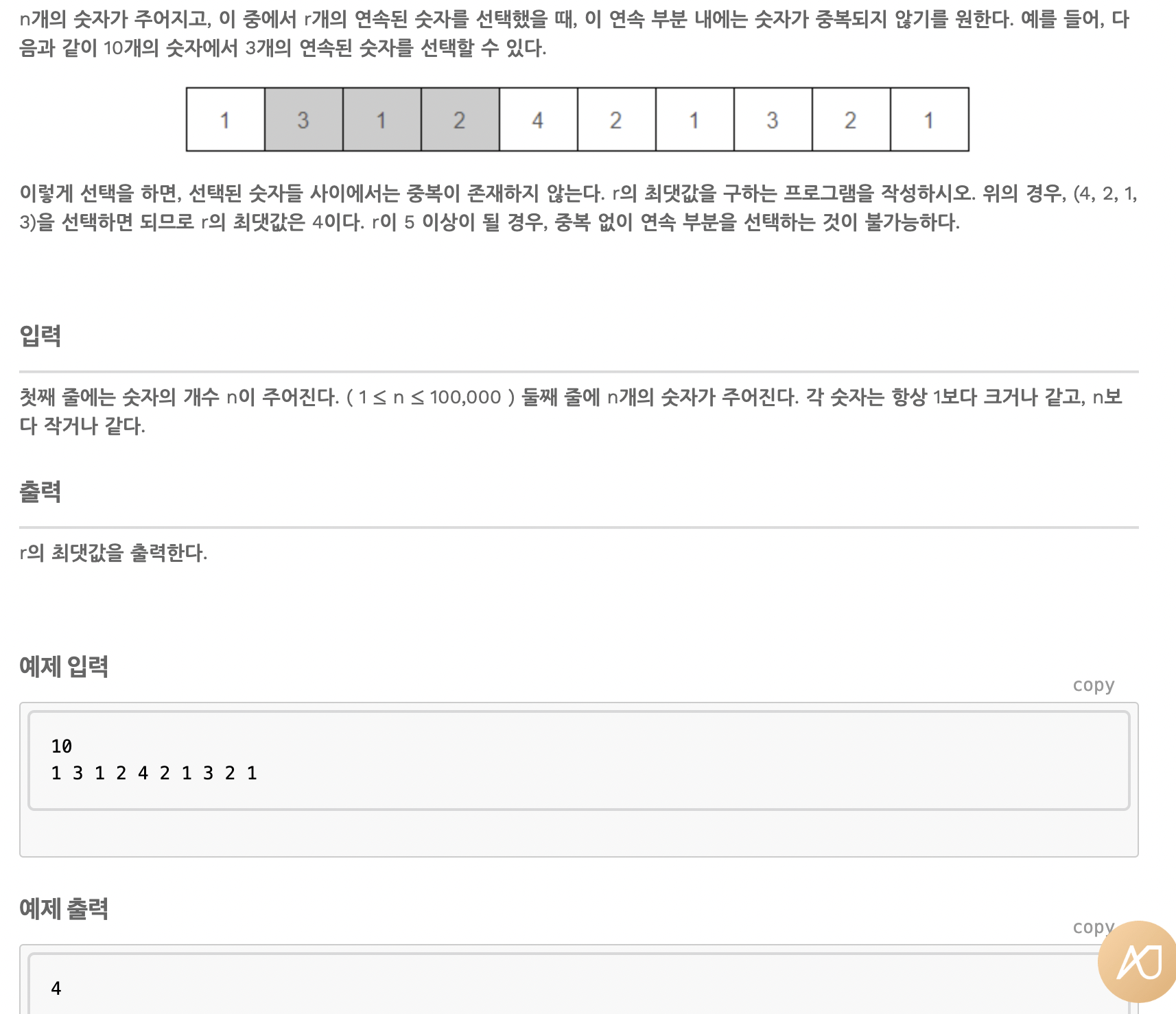
이 문제도 이진 탐색을 사용한다.
처음 이진 탐색을 어떻게 사용할지 의문이 들었는데, r을 찾을 때 이진 탐색을 사용한다.
예를 들어 4번째 줄보다 크다면 1,2,3은 당연하게도 연속되지 않는 수열이 있다.
정답 코드
import java.util.Scanner;
public class Main {
static int n;
static int[] arr;
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
arr = new int[n];
for (int i=0;i<arr.length;i++){
arr[i] = sc.nextInt();
}
int start = 1;
int end = n;
if (!checkLength(start)){
System.out.println(1);
return;
}
if (checkLength(end)){
System.out.println(end);
return;
}
while (start+1<end){
int mid = (start+end)/2;
if (checkLength(mid))start=mid;
else end=mid;
}
System.out.println(start);
}
static boolean checkLength(int length){
int index = 0;
int[] count = new int[n+1];
int overlap =0;
for (int i = index; i<index+length;i++){
count[arr[i]]++;
}
for (int i=1;i<=n;i++){
if (count[i]>=2)overlap++;
}
if (overlap==0)return true;
while (index+length<n){
count[arr[index]]--;
if (count[arr[index]]==1)overlap--;
index++;
count[arr[index+length-1]]++;
if (count[arr[index+length-1]]==2)overlap++;
if (overlap==0)return true;
}
return false;
}
}동작 과정을 보면, 길이 1과 n을 검사하여 중복인 구간이 있는지 없는지를 본다.
1은 중복구간이 될 수가 없기 때문에 start를 1로 설정한다.
n을 검사할 때 중복이 없다면 제일 긴 길이기 때문에 n을 반환한다.
중복인 구간이 없다면 더 큰 구간을 봐서 최댓값을 구해야 한다. 중복인 구간이 있다면 더 작은 값을 확인해야 한다.
중요한 부분은 중복인 구간을 검사할 때 시간을 줄이는 것이다.
count는 해당 숫자가 얼마나 나왔는지 알려준다.
count배열의 값들이 모두 1 이하이면 중복이 없다는 것을 의미한다.