자료구조(Stack&Queue)
스택과 큐는 선형 자료구조이다. (Linear)
스택
스택은 말 그대로 쌓다는 의미를 가지고 있다.
스택은 Last In First Out이다. 즉 마지막에 들어간 값이 제일 처음 나온다.
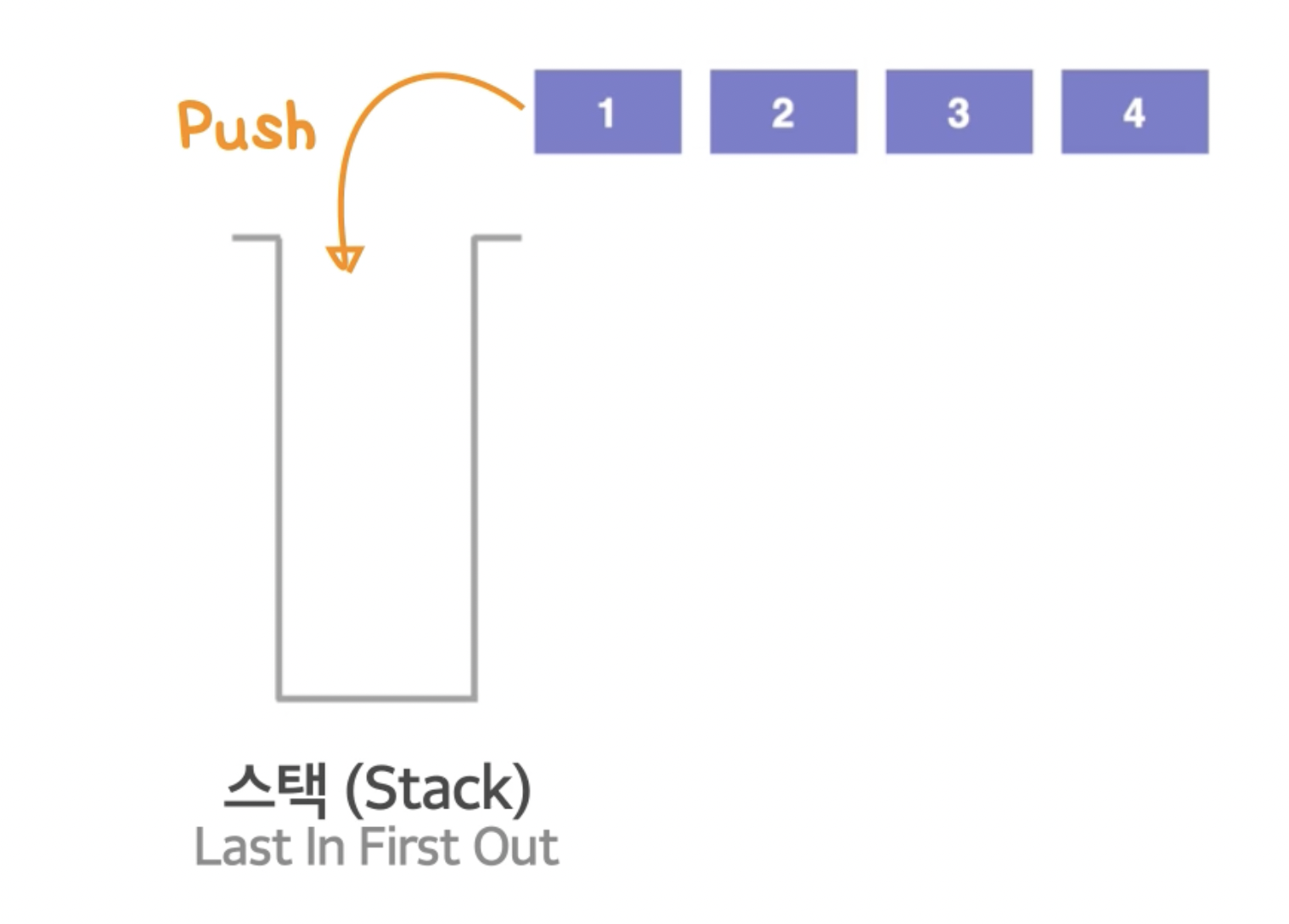
1,2,3,4를 순서대로 넣는다고 생각해보자.
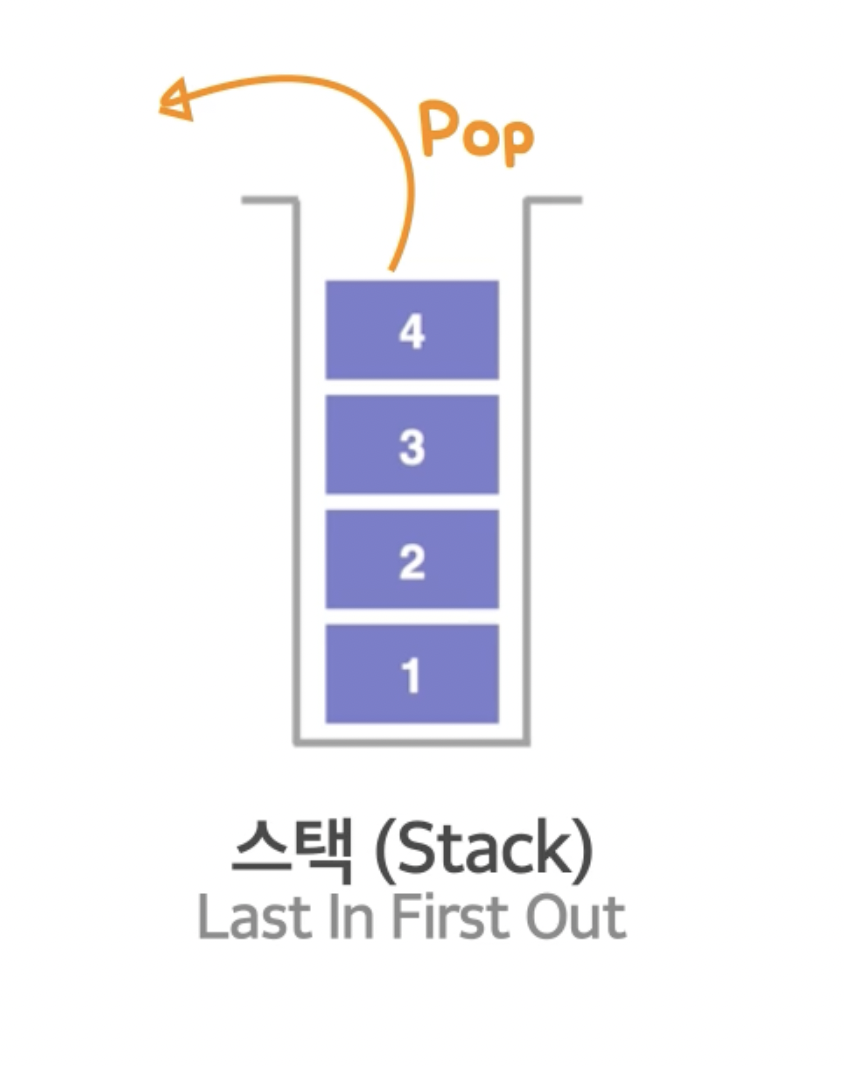
위와 같이 1,2,3,4 순서대로 담기게 된다. 뺄 때는 위에서부터 한 개씩 빼게 된다.
스택을 구현할 때 우리가 생각할 부분은 스택 오버플로우와 스택 언더플로우이다.
오버플로우는 스택이 가득 찼는데, 우리가 원소를 더 넣으려 할 때 발생한다.
언더플로우는 스택이 비었을 때, 우리가 원소를 더 빼려고 할 때 발생한다.
스택 구현
구현하기에 앞서 우리가 어떤 기능을 구현할지 생각해보자.
S를 스택이라 하자
S.create(x) : S의 크기를 x로 지정한다.
S.push(x) : S에 x를 삽입한다.
S.pop : S에서 원소 하나를 제거한다.
S.peek : S의 가장 위에 있는 원소를 반환한다.
S.size : S내에 존재하는 원소의 개수를 반환한다.
package main;
import java.util.Arrays;
import java.util.Scanner;
import static main.Main.*;
public class Main {
static int size;
static int top=-1;
static int[] stack;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
size = sc.nextInt();
stack s = new stack();
s.create(size);
s.push(2);
s.push(4);
s.push(6);
s.push(8);
s.push(10);
System.out.println(Arrays.toString(stack));
s.pop();
System.out.println(Arrays.toString(stack));
System.out.println(s.peek());
System.out.println(s.size());
}
}
class stack {
void create(int size){
stack = new int[size];
}
boolean isStackFull(){
if (top>=size-1)return true;
else return false;
}
boolean isStackEmpty(){
if (top==-1)return true;
else return false;
}
void push(int data){
if (isStackFull()){
System.out.println("Stack is full");
return;
}
top++;
stack[top]=data;
}
void pop(){
if (isStackEmpty()){
System.out.println("Stack is empty");
return;
}
stack[top] = 0;
top--;
}
int peek(){
return stack[top];
}
int size(){
return top+1;
}
}top을 -1로 두어서 스택이 비었다면 top의 위치는 -1이 된다.
값이 0일 때를 빈 값으로 두고 구현하였다.
아래는 스택을 사용하였을 때, 결과이다.
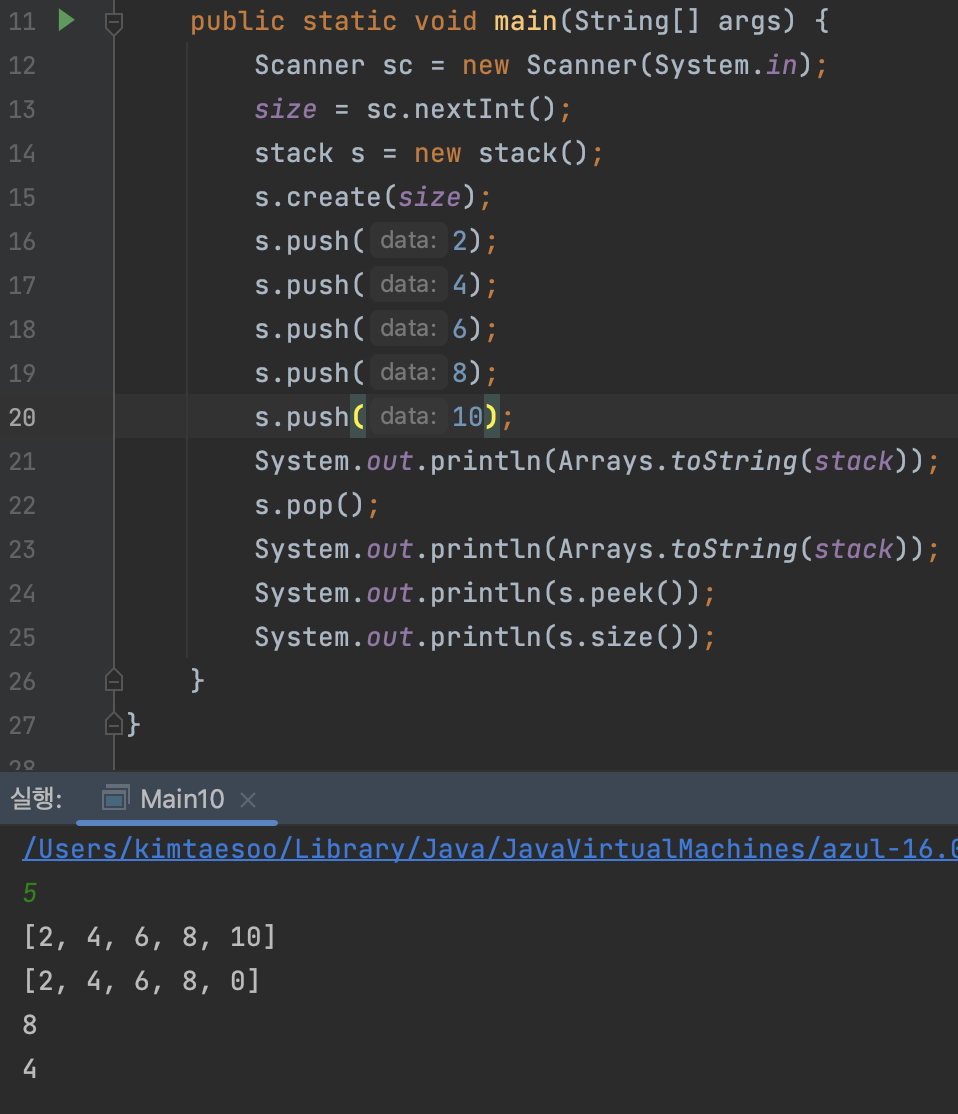
만약 20번째 줄 다음에 한 번 더 push를 한다면 stack is full이라는 말이 나오고 저장을 실패한다.
peek은 맨뒤의 값을 반환해주고, size의 경우 원소의 개수를 반환한다.(0은 빈 값을 의미)
큐
큐는 First In Firsh Out이다. 즉 처음 들어간 값이 처음 나오게 된다.
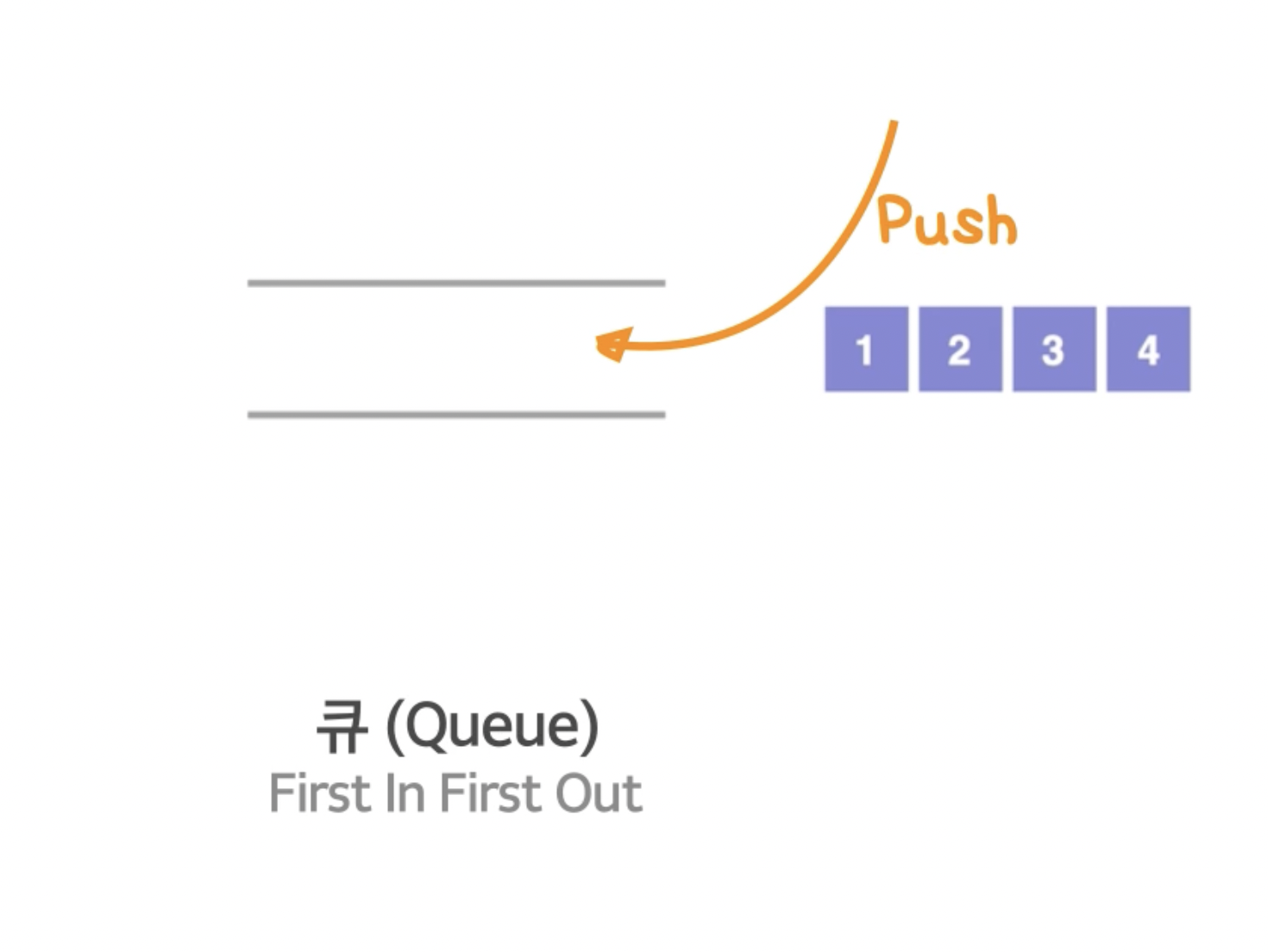
값 1,2,3,4를 순서대로 넣는다고 생각해보자.

큐는 넣은 순서 그대로 1,2,3,4 차례대로 나오게 된다.
큐를 구현할 때 우리가 생각할 부분은 스택 오버플로우이다.
오버플로우는 큐가 가득 찼는데, 우리가 원소를 더 넣으려 할 때 발생한다.
언더플로우는 큐가 비었을 때, 우리가 원소를 더 빼려고 할 때 발생한다.
큐 구현
큐를 구현하기 전에 어떤 기능을 구현할지 생각해보자.
Q를 큐라 하자.
Q.create(x) : Q의 크기를 x로 지정한다.
Q.offer(x) : Q에 x를 삽입한다.
Q.poll() :Q에서 원소 하나를 제거한다.
Q.peek() : Q의 가장 앞에 있는 원소를 반환한다.
Q.size() : Q내에 존재하는 원소의 개수를 반환한다.
package main;
import java.util.Arrays;
import java.util.Scanner;
import static main.Main.*;
public class Main {
static int size;
static int front=-1;
static int rear =-1;
static int[] queue;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
size = sc.nextInt();
main.queue q = new queue();
q.create(size);
q.offer(2);
q.offer(4);
q.offer(6);
q.offer(8);
System.out.println(Arrays.toString(queue));
q.poll();
System.out.println(Arrays.toString(queue));
System.out.println(q.peek());
System.out.println(q.size());
}
}
class queue {
void create(int size){
queue = new int[size];
}
boolean isStackFull(){
if (rear==size-1)return true;
else return false;
}
boolean isStackEmpty(){
if (front==rear)return true;
else return false;
}
void offer(int data){
if (isStackFull()){
System.out.println("Queue is full");
return;
}
rear++;
queue[rear]=data;
}
void poll(){
if (isStackEmpty()){
System.out.println("Queue is empty");
return;
}
front++;
queue[front]=0;
}
int peek(){
return queue[front+1];
}
int size(){
return rear-front;
}
}큐는 front와 rear가 있다. 둘 다 -1로 시작하는데, front는 말 그대로 처음 값을 가리키고 rear는 말 그대로 마지막 값을 가리킨다.
그래서 값을 추가할 때마다 rear의 값이 증가된다. 반대로 front는 뺄 때마다 값이 증가한다.
아래는 큐를 사용했을 때, 결과이다.
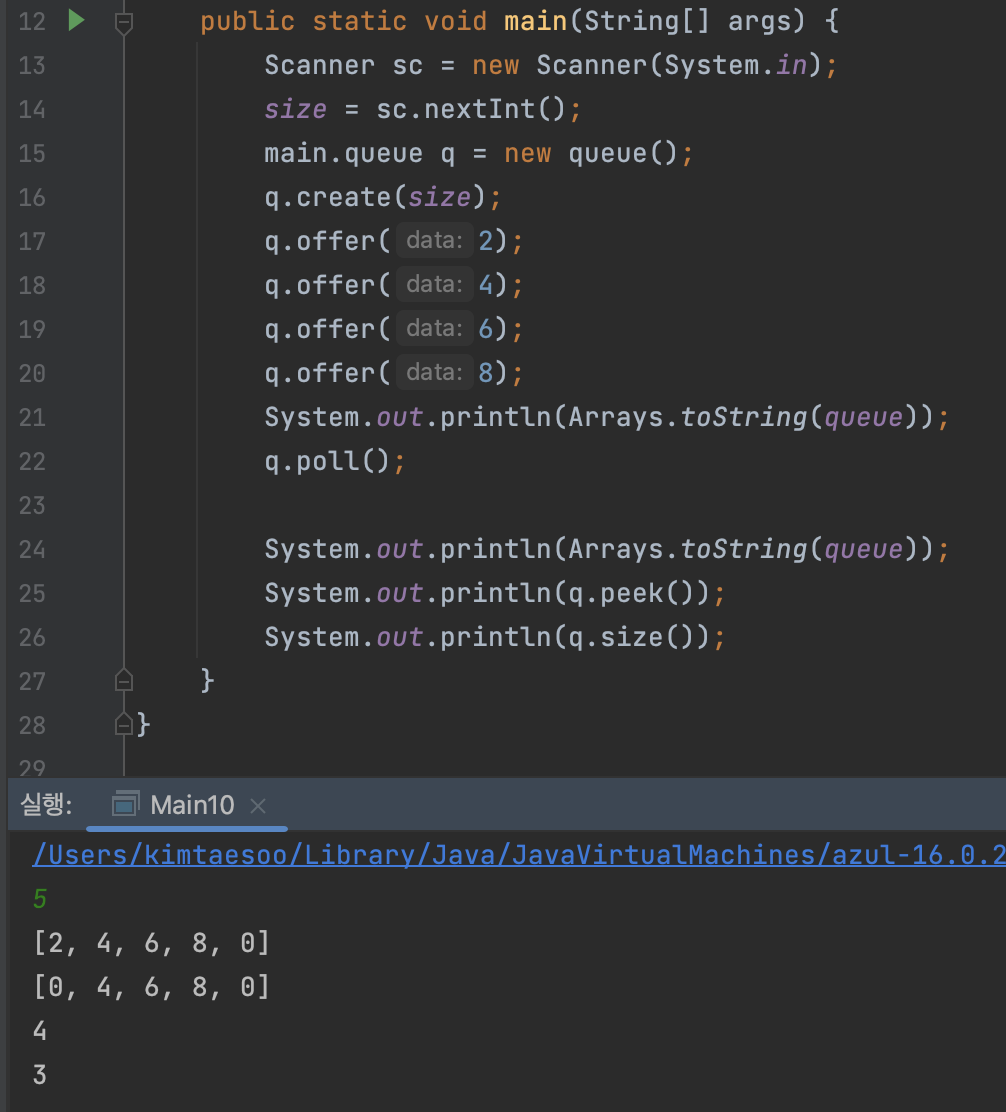
peek의 할 경우 맨 앞의 값을 반환한다. size의 경우 원소의 개수를 반환한다.(0은 빈 값을 의미)
우리가 큐를 구현하면서, 이상한 점을 불편한 점을 느꼈을 것이다.
바로 제거한 앞부분을 더 이상 사용하지 못하게 된다는 것이다.
이러한 문제점은 원형 큐를 사용하여 해결할 수 있다.
원형 큐
원형 큐는 큐의 rear값이나 front값이 사이즈를 넘기면 다시 앞으로 가는 것이다.
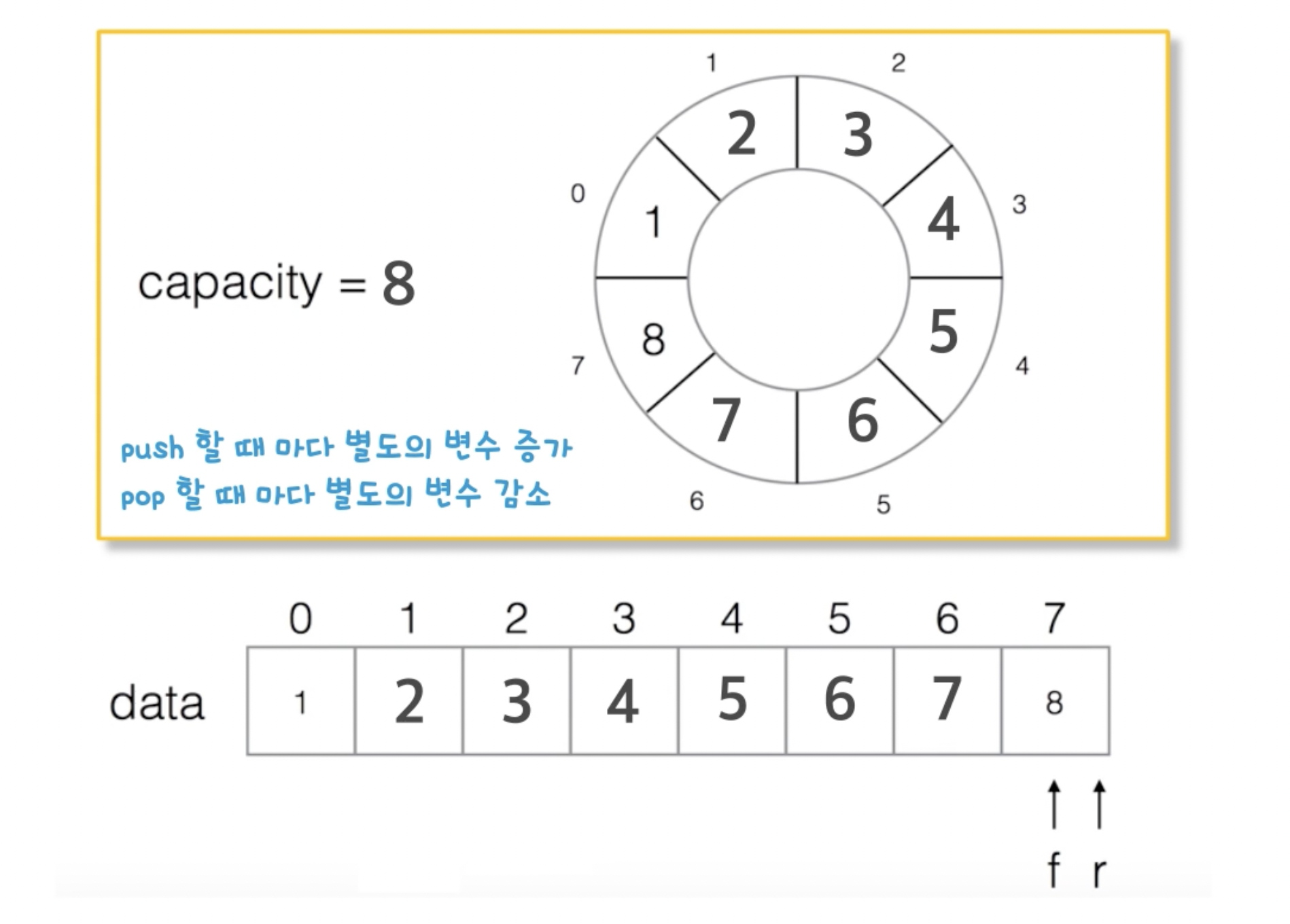
만약 rear == front의 경우 큐가 가득 찬 것이다.
기본 큐에서 코드가 크게 달라진 것은 없다.
package main;
import java.util.Arrays;
import java.util.Scanner;
import static main.Main.*;
public class Main {
static int size;
static int front=-1;
static int rear =-1;
static int[] queue;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
size = sc.nextInt();
main.queue q = new queue();
q.create(size);
q.offer(2);
q.offer(4);
q.offer(6);
q.offer(8);
q.offer(8);
System.out.println(Arrays.toString(queue));
q.poll();
q.poll();
q.poll();
q.offer(10);
q.offer(10);
System.out.println(Arrays.toString(queue));
System.out.println(q.peek());
System.out.println(q.size());
}
}
class queue {
void create(int size){
queue = new int[size];
}
boolean isStackFull(){
if ((rear+1)%size==front)return true;
else return false;
}
boolean isStackEmpty(){
if (front==rear)return true;
else return false;
}
void offer(int data){
if (isStackFull()){
System.out.println("Stack is full");
return;
}
rear = (rear+1)%size;
queue[rear]=data;
}
void poll(){
if (isStackEmpty()){
System.out.println("Stack is empty");
return;
}
front = (front+1)%size;
queue[front]=0;
}
int peek(){
return queue[(front+1)%size];
}
int size(){
if (front<rear)return rear-front;
return (size-front)+rear;
}
}rear나 front값을 +1 하는 과정에서 % size가 추가되었다. 즉 범위를 넘어서면 앞으로 가는 것이다.
아래는 원형 큐를 사용할 때, 결과이다.
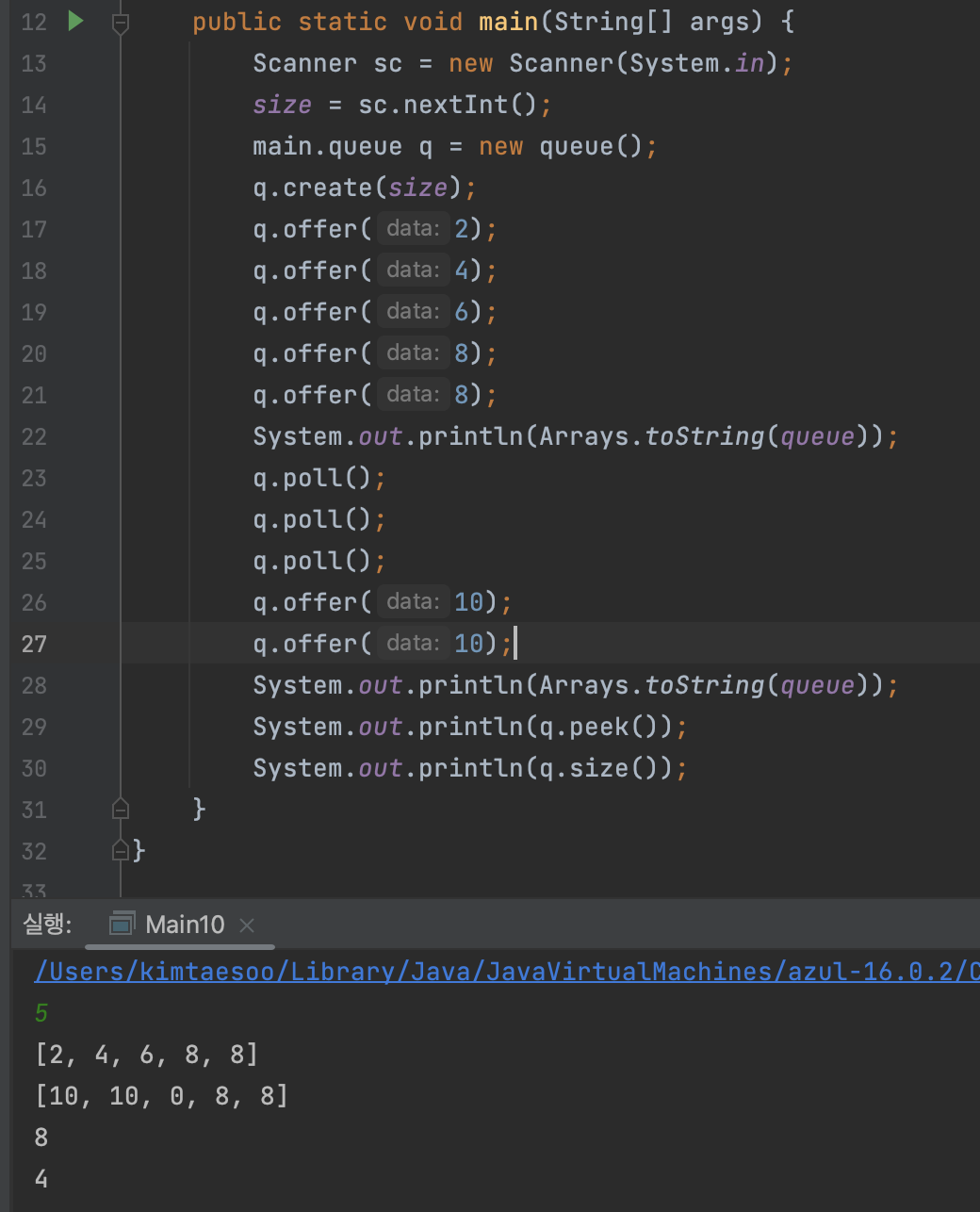
0은 빈 값을 의미한다. 큐가 가득 찬 상태에서 세 개를 제거하고 10을 두 번 추가하니 빈 구간인 앞에서부터 채워진다.
사용 예시 문제를 보자
대표적인 괄호 문제이다.
괄호
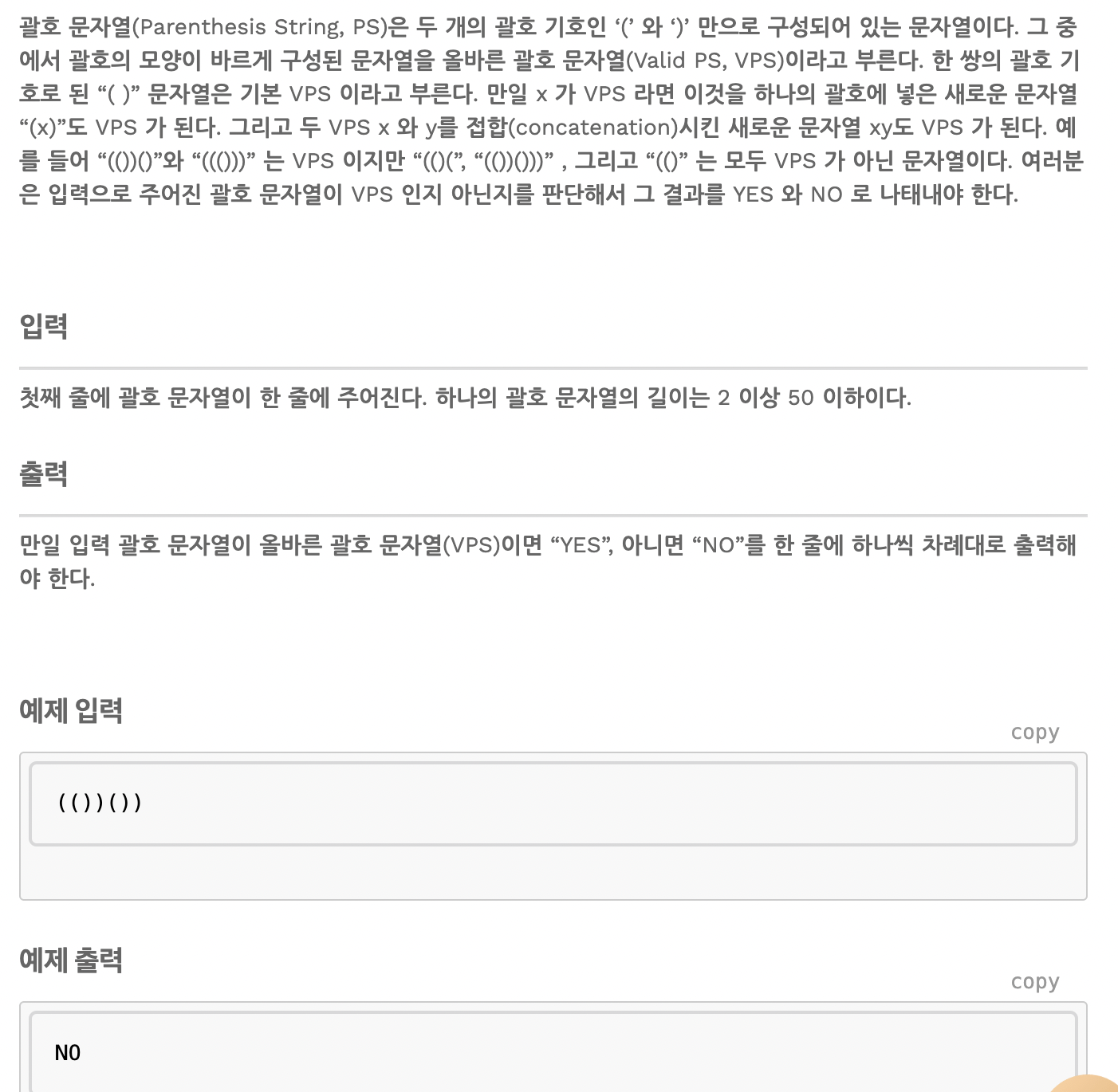
스택의 대표적인 문제이다.
중요한 점은 괄호가 )이면 pop을 해야 하는데, 스택이 비어있다면 오류가 뜨게 된다.
import java.util.Scanner;
import java.util.Stack;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String str = sc.nextLine();
if (stack(str)) System.out.println("YES");
else System.out.println("NO");
}
static boolean stack(String string) {
Stack s = new Stack<>();
for (int i = 0; i < string.length(); i++) {
if (string.charAt(i) == '(') s.push('(');
else if (string.charAt(i) == ')'&&!s.empty()) s.pop();
else if (s.empty()&&string.charAt(i) == ')') return false;
}
if (s.empty())return true;
else return false;
}
}괄호가 남아있다면 false이다. 만약 스택이 비어있는데 )이 나온다면 false이다.
탑
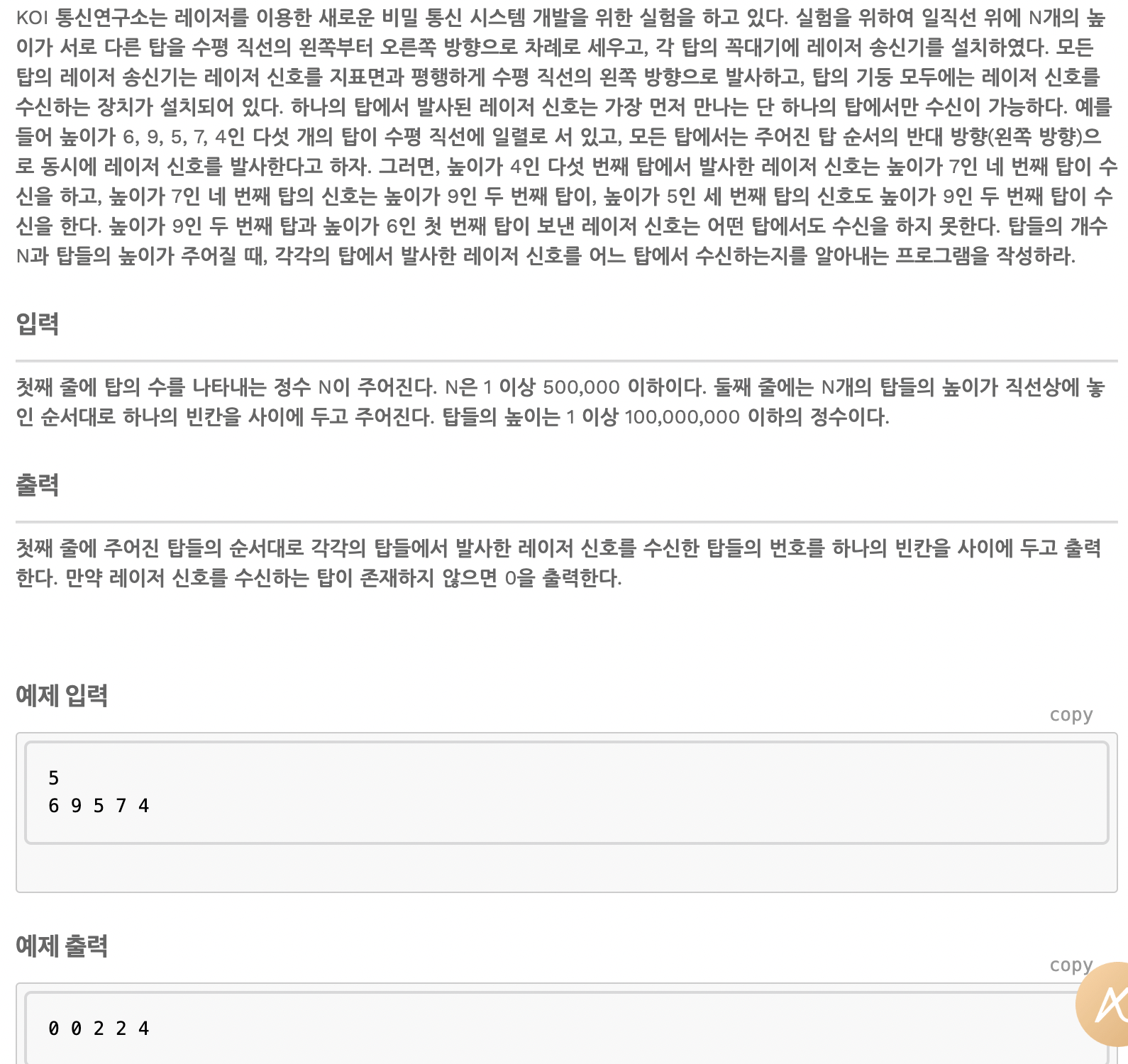
이문제는 스택을 사용한다.
아래는 처음 시도했던 코드이다. 런타임 에러가 뜨지만, 접근방법은 괜찮았다고 생각했었다. 지금 생각해보면 오히려 어렵게 풀은 것 같다.
import java.util.Scanner;
import java.util.Stack;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Stack<Integer>s = new Stack<>();
int n = sc.nextInt();
int[] arr= new int[n+1];
int[] result = new int[n+1];
for (int i=1;i<=n;i++){
arr[i] =sc.nextInt();
}
for (int i=n;i>0;i--){
while (!s.empty()&&arr[s.peek()]<arr[i]){
result[s.pop()] = i;
}
s.push(i);
}
for (int i =1; i<=n;i++){
System.out.print(result[i]+" ");
}
}
}중간에 for문이 가장 중요한 코드이다.
맨뒤의 index부터 시작하게 된다.
처음 시작은 당연하게 while문을 들어가지 않는다. 스택에 마지막 인덱스를 넣는다.
그리고 앞의 값과 비교한 뒤, 앞의 값이 더 크면 pop 시키고, 인덱스를 result에 저장한다.
생각보다 이해하기 어려울 수 있다.
아래 그림을 보면서 이해해보자
arr ={6,9,5,7,4}라고 가정한다. 또한 i는 1부터 n까지 저장된다. 즉 배열의 크기는 n+1이라 생각하자.

처음 i는 5이다. while문은 당연하게 실행되지 않고(스택이 비어있으므로), 스택에 5가 저장된다.
이후 i가 4일 때, 지금 인덱스의 배열의 값(7)이 스택에 저장된 인덱스의 값이(4) 보다 크기 때문에,
스택의 맨 위 값을 지우고, 스택에 저장된 값을 인덱스로 한 result에 저장한다.
이후 스택에 4를 추가한다.(실제 스택에 index값을 저장하는 것이 맞다. 이해를 돕기 위해 arr [index]를 저장해둔 값을 적었다.)
위의 말을 수식으로 나타내면
i =5 이므로 while문은 실행되지 않고, s.push(5), i=4일 때, arr [4]>arr [5]이므로 result [5] = 4가 된다. 이후 s.push(4)를 한다.
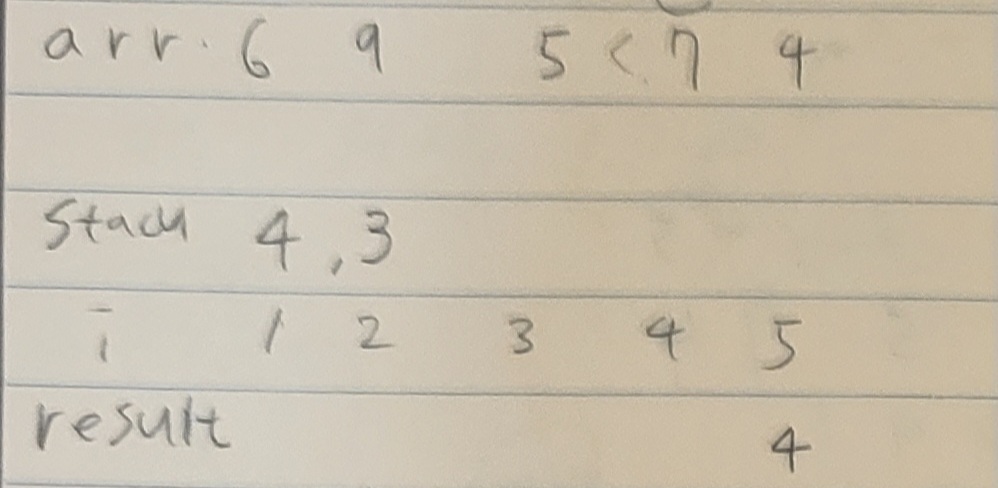
다음은 i가 3일 때이다. 스택에는 4가 추가되어있고, arr [3]이 arr [4]보다 작으므로, 스택에 3을 추가하고 끝난다.

i=2일 때를 보자. arr [2]가 arr [3], arr [4]보다 크므로, result [4]=2, result [3]=2를 해주고, s.push(2)를한다.
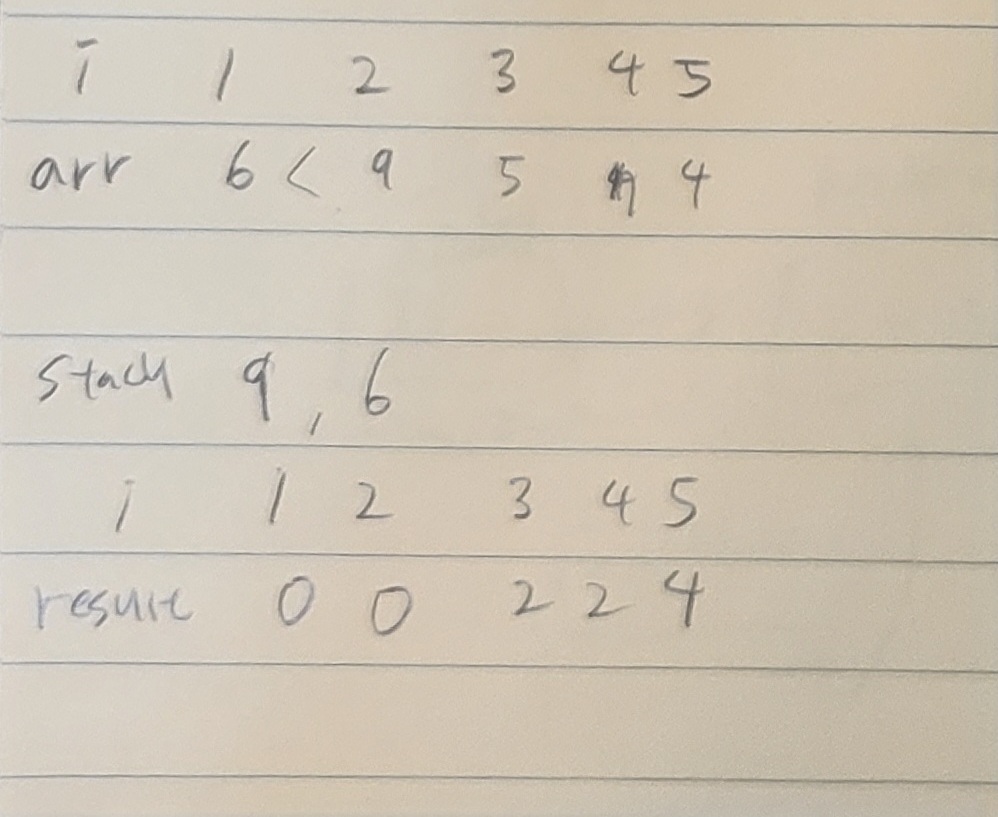
이후 스택에는 2,1이 남아있는 채로 for문이 종료된다. (이해를 돕기 위해 스택에 arr [index]를 적어두었다.)
따라서 result의 첫 번째와 두 번째는 초기값인 0으로 종료된다.
다음은 정답 코드이다.
package main;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Stack;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int num = Integer.parseInt(br.readLine());
Stack<int[]> stack = new Stack<>();
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<num; i++) {
int n = Integer.parseInt(st.nextToken());
while(!stack.isEmpty()) {
if(stack.peek()[0] < n)
stack.pop();
else {
System.out.print(stack.peek()[1] + " ");
stack.push(new int[] {n, i+1});
break;
}
}
if(stack.empty())
System.out.print("0 ");
stack.push(new int[] {n, i+1});
}
}
}스택 자체를 int형 배열 값을 저장하게 만들었다.
반복문이 중요하다.
가장 앞의 탑이 n보다 작으면, 앞의 값들은 의미가 없으므로 pop 한다.
만약 n보다 크다면 해당 위치를 출력한다.
만약 스택을 전부 비워도 큰 값을 못 찾는다면 -> 스택이 비었다면 0을 출력한다.
그리고 반복문이 끝날 때마다 스택에 탑의 높이와 위치를 저장시킨다.
배운 점
스택과 큐를 기존에 알고 있었지만, 직접 구현은 이번이 처음이었다. 직접 구현해보니 생각보다 신경 써야 할 부분이 많았다.
스택을 이용한 문제들을 풀어봤는데, Stack에 int형 배열을 저장할 수 있다는 사실을 처음 알았다.
또한 스택을 잘 이용해서 문제를 풀면 시간 복잡도에서 큰 이점이 있다는 사실을 알았다.
자료구조에 더욱 익숙해지자