https://leetcode.com/problems/knight-probability-in-chessboard/
Knight Probability in Chessboard - LeetCode
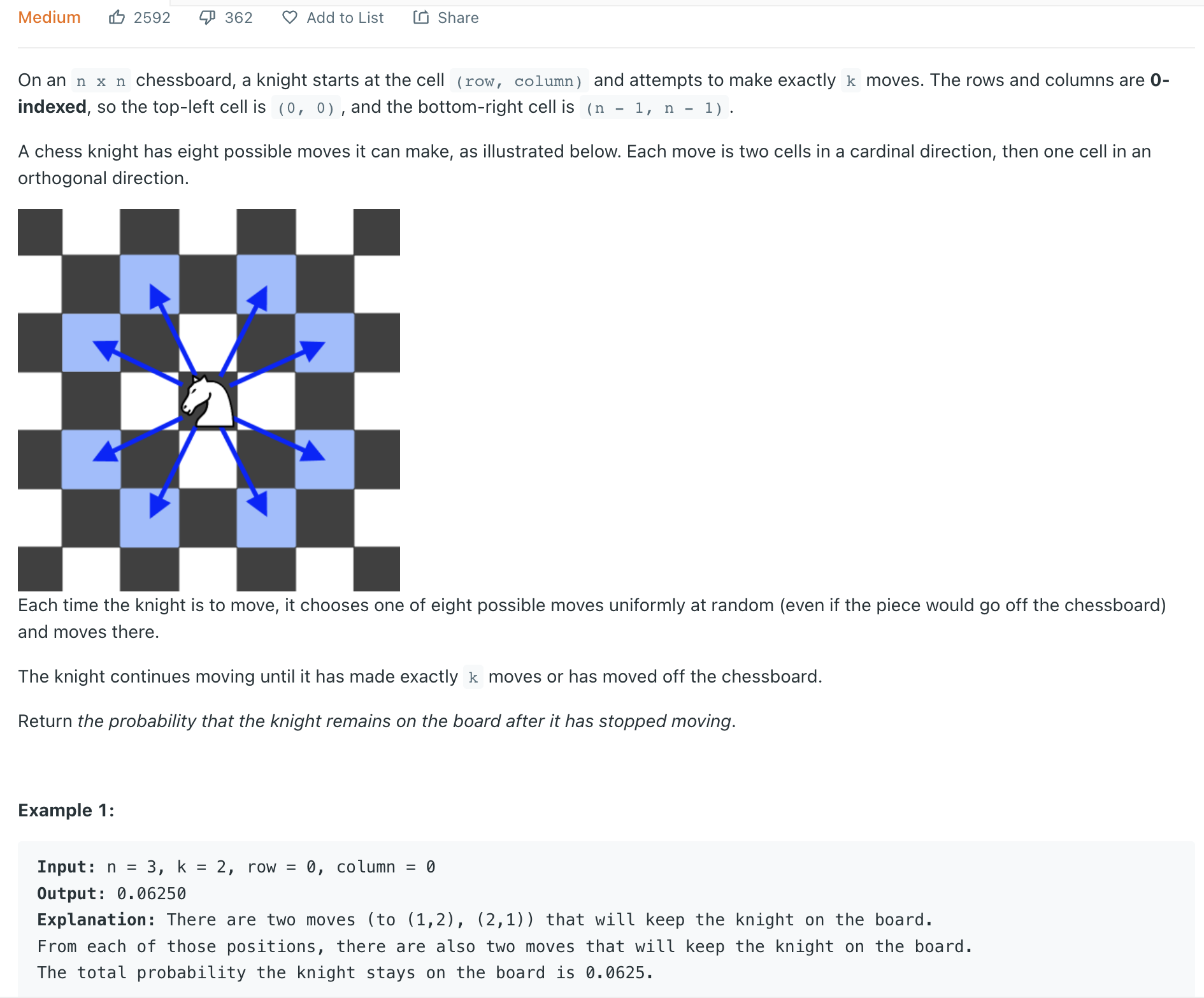
Can you solve this real interview question? Knight Probability in Chessboard - On an n x n chessboard, a knight starts at the cell (row, column) and attempts to make exactly k moves. The rows and columns are 0-indexed, so the top-left cell is (0, 0), and t
leetcode.com
오늘 문제는 dp를 이용한 문제이다.
처음에는 단순하게 bfs를 사용하여 풀려고 했는데, k의 값의 범위가 커져서 시간초과가 떠버렸다.
bfs로는 풀 수 없는 문제이다.
핵심
이 문제는 dp를 사용하여 풀 수 있다.
핵심은 현재의 위치에서 이전의 위치의 값을 더하는 방식으로 풀 수 있다.
이는 글로는 이해가 잘 안 되고, 코드를 보면 쉽게 이해할 수 있다.
그전에 우선 bfs로 풀어본 코드를 파악해 보자.
시간 초과가 나온 코드
class Solution {
private int answer = 0;
int[][] directions = {{1, 2}, {1, -2}, {-1, 2}, {-1, -2},
{2, 1}, {2, -1}, {-2, 1}, {-2, -1}};
public double knightProbability(int n, int k, int row, int column) {
bfs(n, k, row, column);
return answer / Math.pow(8, k);
}
private void bfs(int n, int k, int row, int column) {
Queue<int[]> q = new LinkedList<>();
q.offer(new int[]{row, column, 0});
while (!q.isEmpty()) {
int[] now = q.poll();
int x = now[0];
int y = now[1];
int count = now[2];
if (count == k) {
answer++;
continue;
}
for (int[] direction : directions) {
int moveX = x + direction[0];
int moveY = y + direction[1];
if (0 <= moveX && moveX < n && 0 <= moveY && moveY < n) {
q.offer(new int[]{moveX, moveY, count + 1});
}
}
}
}
}해설
사실 bfs가 직관적으로 이해하기 쉽다. 간단하기도 하기에 이 방법을 사용하려 했다.
코드는 단순히 실제로 기물을 이동시키는 것이다.
이동하는 도중에 체스판을 벗어나면 그 경우는 버리게 된다.
만약 이동 횟수가 k와 동일하게 된다면 answer을 높인다.
실제 이동 경우의 수는 8^k이기에 이를 나눈 값이 답이 된다.
하지만 실제로 기물을 이동해야하기에 k 값이 10번만 되어도 10억 번이 넘는 이동을 수행할 수 있다.
정답 코드
public class Solution {
public double knightProbability(int n, int k, int row, int column) {
int[][] directions = {{1, 2}, {1, -2}, {-1, 2}, {-1, -2},
{2, 1}, {2, -1}, {-2, 1}, {-2, -1}};
double[][][] dp = new double[k + 1][n][n];
dp[0][row][column] = 1;
for (int moves = 1; moves <= k; moves++) {
for (int x = 0; x < n; x++) {
for (int y = 0; y < n; y++) {
for (int[] direction : directions) {
int preX = x - direction[0];
int preY = y - direction[1];
if (0 <= preX && preX < n && 0 <= preY && preY < n) {
dp[moves][x][y] += dp[moves - 1][preX][preY] / 8.0;
}
}
}
}
}
double answer = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
answer += dp[k][i][j];
}
}
return answer;
}
}해설
앞선 bfs 방식으로는 풀 수 없기에 dp를 사용하였다.
현재의 위치에서 이전의 이동값을 더하면서 진행하게 된다.
첫 번째 경우만 예시를 들면 n = 3, k = 1, row = 0, column = 0이라고 한다면
각각의 체스판을 탐색하면서 이전에서 올 수 있는 값들을 더한다.
즉 x = 2, y = 1, move = 1에서 1/8이 저장되고 x =1, y =2, move = 1에서 1/8이 저장된다.
이런 식으로 k번을 반복하여 모든 체스판의 값들을 더하면 정답을 구할 수 있다.
배운 점
우선 요즘 자바를 잘 다루지 않았지만, 아직까지는 익숙하게 풀 수 있다고 생각한다.
하지만 문제의 난이도를 보고 당연하게도 bfs일 것이라는 생각을 가지고 풀게 되었다.
이러한 생각이 나에게는 안 좋은 영향을 끼치는 것 같다.
문제의 함정을 생각하고 풀자.
'PS > 알고리즘 문제풀이' 카테고리의 다른 글
| [백준] 13460번 구슬 탈출2(java) (0) | 2023.08.08 |
|---|---|
| [프로그래머스] [3차] 방금그곡(java) (0) | 2023.08.06 |
| [LeetCode] 2024 - Maximize the Confusion of an Exam(java) (0) | 2023.07.07 |
| [LeetCode] 209 - Minimum Size Subarray Sum(java) (0) | 2023.07.06 |
| [LeetCode] 1601 - Maximum Number of Achievable Transfer Requests(java) (0) | 2023.07.02 |
https://leetcode.com/problems/knight-probability-in-chessboard/
Knight Probability in Chessboard - LeetCode
Can you solve this real interview question? Knight Probability in Chessboard - On an n x n chessboard, a knight starts at the cell (row, column) and attempts to make exactly k moves. The rows and columns are 0-indexed, so the top-left cell is (0, 0), and t
leetcode.com

오늘 문제는 dp를 이용한 문제이다.
처음에는 단순하게 bfs를 사용하여 풀려고 했는데, k의 값의 범위가 커져서 시간초과가 떠버렸다.
bfs로는 풀 수 없는 문제이다.
핵심
이 문제는 dp를 사용하여 풀 수 있다.
핵심은 현재의 위치에서 이전의 위치의 값을 더하는 방식으로 풀 수 있다.
이는 글로는 이해가 잘 안 되고, 코드를 보면 쉽게 이해할 수 있다.
그전에 우선 bfs로 풀어본 코드를 파악해 보자.
시간 초과가 나온 코드
class Solution {
private int answer = 0;
int[][] directions = {{1, 2}, {1, -2}, {-1, 2}, {-1, -2},
{2, 1}, {2, -1}, {-2, 1}, {-2, -1}};
public double knightProbability(int n, int k, int row, int column) {
bfs(n, k, row, column);
return answer / Math.pow(8, k);
}
private void bfs(int n, int k, int row, int column) {
Queue<int[]> q = new LinkedList<>();
q.offer(new int[]{row, column, 0});
while (!q.isEmpty()) {
int[] now = q.poll();
int x = now[0];
int y = now[1];
int count = now[2];
if (count == k) {
answer++;
continue;
}
for (int[] direction : directions) {
int moveX = x + direction[0];
int moveY = y + direction[1];
if (0 <= moveX && moveX < n && 0 <= moveY && moveY < n) {
q.offer(new int[]{moveX, moveY, count + 1});
}
}
}
}
}해설
사실 bfs가 직관적으로 이해하기 쉽다. 간단하기도 하기에 이 방법을 사용하려 했다.
코드는 단순히 실제로 기물을 이동시키는 것이다.
이동하는 도중에 체스판을 벗어나면 그 경우는 버리게 된다.
만약 이동 횟수가 k와 동일하게 된다면 answer을 높인다.
실제 이동 경우의 수는 8^k이기에 이를 나눈 값이 답이 된다.
하지만 실제로 기물을 이동해야하기에 k 값이 10번만 되어도 10억 번이 넘는 이동을 수행할 수 있다.
정답 코드
public class Solution {
public double knightProbability(int n, int k, int row, int column) {
int[][] directions = {{1, 2}, {1, -2}, {-1, 2}, {-1, -2},
{2, 1}, {2, -1}, {-2, 1}, {-2, -1}};
double[][][] dp = new double[k + 1][n][n];
dp[0][row][column] = 1;
for (int moves = 1; moves <= k; moves++) {
for (int x = 0; x < n; x++) {
for (int y = 0; y < n; y++) {
for (int[] direction : directions) {
int preX = x - direction[0];
int preY = y - direction[1];
if (0 <= preX && preX < n && 0 <= preY && preY < n) {
dp[moves][x][y] += dp[moves - 1][preX][preY] / 8.0;
}
}
}
}
}
double answer = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
answer += dp[k][i][j];
}
}
return answer;
}
}해설
앞선 bfs 방식으로는 풀 수 없기에 dp를 사용하였다.
현재의 위치에서 이전의 이동값을 더하면서 진행하게 된다.
첫 번째 경우만 예시를 들면 n = 3, k = 1, row = 0, column = 0이라고 한다면
각각의 체스판을 탐색하면서 이전에서 올 수 있는 값들을 더한다.
즉 x = 2, y = 1, move = 1에서 1/8이 저장되고 x =1, y =2, move = 1에서 1/8이 저장된다.
이런 식으로 k번을 반복하여 모든 체스판의 값들을 더하면 정답을 구할 수 있다.
배운 점
우선 요즘 자바를 잘 다루지 않았지만, 아직까지는 익숙하게 풀 수 있다고 생각한다.
하지만 문제의 난이도를 보고 당연하게도 bfs일 것이라는 생각을 가지고 풀게 되었다.
이러한 생각이 나에게는 안 좋은 영향을 끼치는 것 같다.
문제의 함정을 생각하고 풀자.
'PS > 알고리즘 문제풀이' 카테고리의 다른 글
| [백준] 13460번 구슬 탈출2(java) (0) | 2023.08.08 |
|---|---|
| [프로그래머스] [3차] 방금그곡(java) (0) | 2023.08.06 |
| [LeetCode] 2024 - Maximize the Confusion of an Exam(java) (0) | 2023.07.07 |
| [LeetCode] 209 - Minimum Size Subarray Sum(java) (0) | 2023.07.06 |
| [LeetCode] 1601 - Maximum Number of Achievable Transfer Requests(java) (0) | 2023.07.02 |