https://www.acmicpc.net/problem/11729
11729번: 하노이 탑 이동 순서
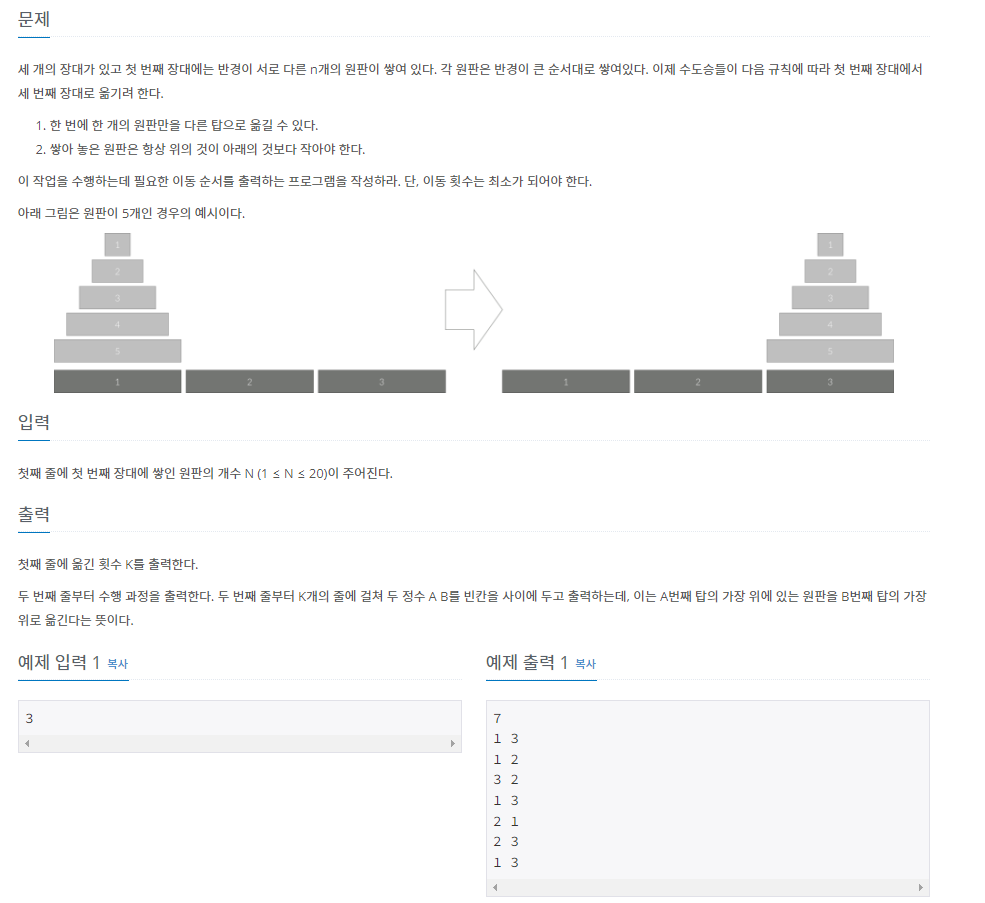
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
백준 11729번 하노이 탑 이동 순서 문제 링크입니다.
핵심
첫 번째 칸에 있는 원판을 마지막 칸으로 옮기는 것인데, 작은 원판 위에 큰 원판이 올라갈 수 없고, 한 번에 1개씩 옮길 수 있다. 재귀 호출을 통해 해결할 수 있다.
정답 코드
package main;
import java.io.*;
public class Main {
public static StringBuilder sb = new StringBuilder();
public static void main(String[] args)throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
sb.append((int)Math.pow(2,N)-1).append('\n');
hanoi(1,2,3,N);
System.out.println(sb);
}
static void hanoi(int from ,int m ,int to ,int N){
if(N==0)return;
hanoi(from, to, m, N-1);
sb.append(from+" "+to+'\n');
hanoi(m,from,to,N-1);
}
}
해설
코드만 보면 재귀 함수가 나와 매우 어렵게 느껴질 수 있다. 필자 또한 이해하는데 오랜 시간이 걸렸다.
옮긴 횟수의 경우에는 append 될 때마다 count를 1씩 추가할 수도 있겠지만, 하노이의 공식대로 2^n -1을 사용하였다.
위 코드는 사실 hanoi 메서드 부분만 해석 가능하다면, 끝난 것이다.
N개의 원판이 있다고 하자. 그럼 우리는 마지막 N번째 원판을 제외하고, 나머지 N-1개의 원판은 중간지점으로 옮겨져 있어야 하고, 그 이후에 마지막 N번째 원판을 목표지점으로 옮긴 뒤, N-1개의 원판 모두 목표지점으로 옮기면 된다.
메서드 실행 순서가 이해하는데 어려움을 겪었다.
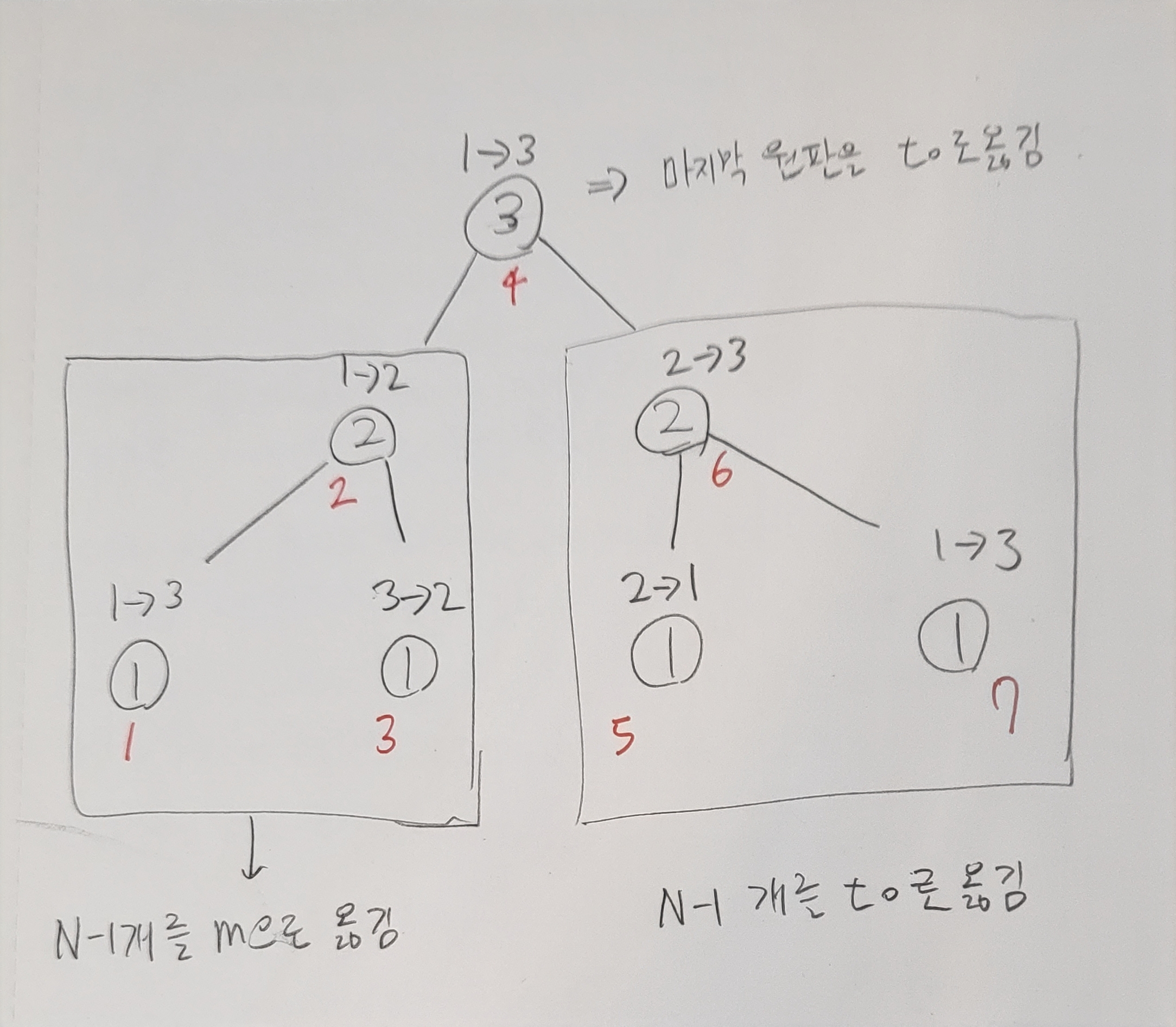
위의 그림은 재귀 함수의 값 N에 3을 대입했을 때이다.
빨간색 숫자는 실행 순서이다. 재귀 함수가 어렵다고 느껴진다면, 그림을 그리면서 풀어보는 것도 괜찮은 방법이다.
위에 숫자-> 숫자는 from->to를 나타낸 것이고, 동그라미 안의 숫자는 원판 번호라고 생각하면 된다.
N=3이므로 3번 원판이 가장 아래에 있다는 뜻이다.
코드와 그림을 보고 비교해보면서 순서대로 실행 과정을 생각해보는 것이 크게 도움이 될 것이다.
개선점이나 오류가 있다면, 댓글 부탁드립니다.
'PS > 알고리즘 문제풀이' 카테고리의 다른 글
| [백준]9663번 N-Queen(java) (0) | 2022.07.24 |
|---|---|
| [백준]14888번 연산자 끼워넣기(java) (0) | 2022.07.24 |
| [백준]10828번 스택(java) (0) | 2022.07.21 |
| [백준]1620번 나는야 포켓몬 마스터 이다솜(java) (0) | 2022.07.18 |
| [백준]2004번 조합0의 개수(java) (0) | 2022.07.17 |
https://www.acmicpc.net/problem/11729
11729번: 하노이 탑 이동 순서
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
백준 11729번 하노이 탑 이동 순서 문제 링크입니다.

핵심
첫 번째 칸에 있는 원판을 마지막 칸으로 옮기는 것인데, 작은 원판 위에 큰 원판이 올라갈 수 없고, 한 번에 1개씩 옮길 수 있다. 재귀 호출을 통해 해결할 수 있다.
정답 코드
package main;
import java.io.*;
public class Main {
public static StringBuilder sb = new StringBuilder();
public static void main(String[] args)throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
sb.append((int)Math.pow(2,N)-1).append('\n');
hanoi(1,2,3,N);
System.out.println(sb);
}
static void hanoi(int from ,int m ,int to ,int N){
if(N==0)return;
hanoi(from, to, m, N-1);
sb.append(from+" "+to+'\n');
hanoi(m,from,to,N-1);
}
}
해설
코드만 보면 재귀 함수가 나와 매우 어렵게 느껴질 수 있다. 필자 또한 이해하는데 오랜 시간이 걸렸다.
옮긴 횟수의 경우에는 append 될 때마다 count를 1씩 추가할 수도 있겠지만, 하노이의 공식대로 2^n -1을 사용하였다.
위 코드는 사실 hanoi 메서드 부분만 해석 가능하다면, 끝난 것이다.
N개의 원판이 있다고 하자. 그럼 우리는 마지막 N번째 원판을 제외하고, 나머지 N-1개의 원판은 중간지점으로 옮겨져 있어야 하고, 그 이후에 마지막 N번째 원판을 목표지점으로 옮긴 뒤, N-1개의 원판 모두 목표지점으로 옮기면 된다.
메서드 실행 순서가 이해하는데 어려움을 겪었다.

위의 그림은 재귀 함수의 값 N에 3을 대입했을 때이다.
빨간색 숫자는 실행 순서이다. 재귀 함수가 어렵다고 느껴진다면, 그림을 그리면서 풀어보는 것도 괜찮은 방법이다.
위에 숫자-> 숫자는 from->to를 나타낸 것이고, 동그라미 안의 숫자는 원판 번호라고 생각하면 된다.
N=3이므로 3번 원판이 가장 아래에 있다는 뜻이다.
코드와 그림을 보고 비교해보면서 순서대로 실행 과정을 생각해보는 것이 크게 도움이 될 것이다.
개선점이나 오류가 있다면, 댓글 부탁드립니다.
'PS > 알고리즘 문제풀이' 카테고리의 다른 글
| [백준]9663번 N-Queen(java) (0) | 2022.07.24 |
|---|---|
| [백준]14888번 연산자 끼워넣기(java) (0) | 2022.07.24 |
| [백준]10828번 스택(java) (0) | 2022.07.21 |
| [백준]1620번 나는야 포켓몬 마스터 이다솜(java) (0) | 2022.07.18 |
| [백준]2004번 조합0의 개수(java) (0) | 2022.07.17 |
