우선 완전 탐색 알고리즘이란 가능한 모든 경우를 탐색하는 것이다.
아래의 체스 문제를 생각해보면, 룩이 이동 가능한 경우를 모두 탐색해보면 된다.

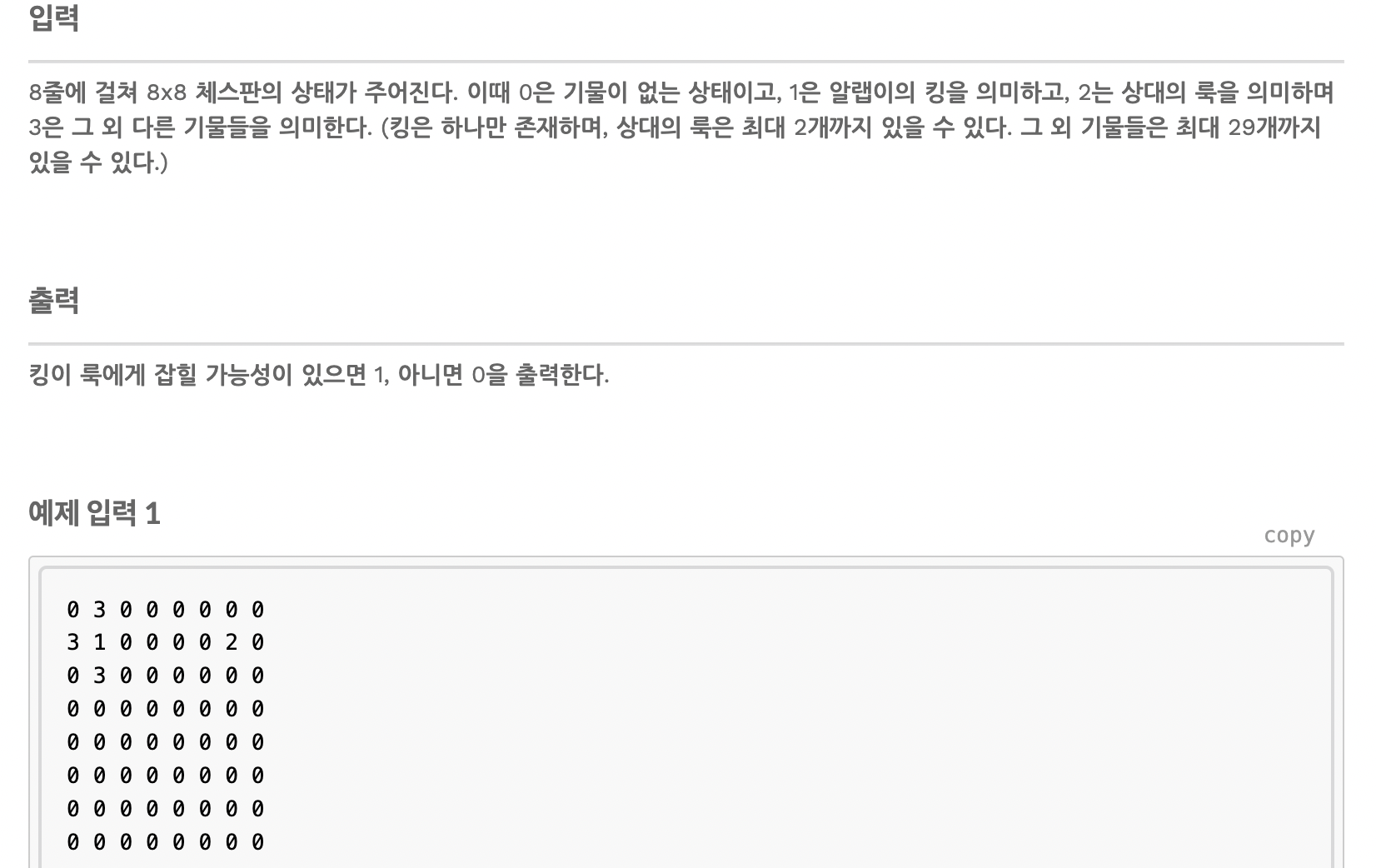
이때 출력은 1이다.
핵심
이 문제를 풀 때, 어떤 것을 기준으로 할까에 따라 풀이가 살짝 달라진다. 룩을 기준으로 하여, 룩의 이동경로 중
킹이 있다면 1 없다면 0을 출력하면 된다.
정답 코드
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int[][] arr = new int[8][8];
int[] rookX = new int[2];
int[] rookY = new int[2];
int count=0;
for (int i=0; i<8;i++){
for (int j=0;j<8;j++){
arr[i][j] =sc.nextInt();
if (arr[i][j]==2){
rookX[count]=j;
rookY[count]=i;
count++;
}
}
}
boolean check = false;
for (int k=0; k<2;k++) {
int x = rookX[k];
int y = rookY[k];
for (int i = x + 1; i < 8; i++) {
if (arr[y][i] == 1) check = true;
else if (arr[y][i] == 3) break;
}
for (int i = y - 1; i >= 0; i--) {
if (arr[i][x] == 1) check = true;
else if (arr[i][x] == 3) break;
}
for (int i = x - 1; i >= 0; i--) {
if (arr[y][i] == 1) check = true;
else if (arr[y][i] == 3) break;
}
for (int i = y + 1; i < 8; i++) {
if (arr[i][x] == 1) check = true;
else if (arr[i][x] == 3) break;
}
}
if (check) System.out.println(1);
else System.out.println(0);
}
}해설
체스판이 8*8이므로 이중 배열의 크기를 [8][8]로 잡는다.
그 후 룩의 개수가 2개일 수도 있으므로 , 룩의 각 x, y좌표를 저장할 배열을 선언한다.
값을 넣는다. 값을 넣을 때, 룩의 값을 저장할 때, x, y좌표를 넣는다.
이후 룩의 좌표에서 오른쪽, 왼쪽, 위, 아래로 이동하면서,
킹을 만나면, check를 true로 바꿔준다.
만약 3을 만나면, 즉 장애물을 만난다면 break를 한다.
룩의 수가 2개일 수도 있으므로, k값이 증가하면, 2번째 룩의 이동경로를 탐색한다.
개선점이나 오류가 있다면, 댓글 부탁드립니다.
'PS > 알고리즘 문제풀이' 카테고리의 다른 글
| *완전 탐색* attackRange (1) | 2022.09.15 |
|---|---|
| *완전탐색* colorpaper (0) | 2022.09.14 |
| [백준]1213번 팰린드롬 만들기(java) (0) | 2022.09.10 |
| *배열* arr3 (java, 알고리즘) (0) | 2022.09.04 |
| *다중 반복문* 숫자 피라미드(java, 알고리즘) (0) | 2022.09.04 |
우선 완전 탐색 알고리즘이란 가능한 모든 경우를 탐색하는 것이다.
아래의 체스 문제를 생각해보면, 룩이 이동 가능한 경우를 모두 탐색해보면 된다.


이때 출력은 1이다.
핵심
이 문제를 풀 때, 어떤 것을 기준으로 할까에 따라 풀이가 살짝 달라진다. 룩을 기준으로 하여, 룩의 이동경로 중
킹이 있다면 1 없다면 0을 출력하면 된다.
정답 코드
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int[][] arr = new int[8][8];
int[] rookX = new int[2];
int[] rookY = new int[2];
int count=0;
for (int i=0; i<8;i++){
for (int j=0;j<8;j++){
arr[i][j] =sc.nextInt();
if (arr[i][j]==2){
rookX[count]=j;
rookY[count]=i;
count++;
}
}
}
boolean check = false;
for (int k=0; k<2;k++) {
int x = rookX[k];
int y = rookY[k];
for (int i = x + 1; i < 8; i++) {
if (arr[y][i] == 1) check = true;
else if (arr[y][i] == 3) break;
}
for (int i = y - 1; i >= 0; i--) {
if (arr[i][x] == 1) check = true;
else if (arr[i][x] == 3) break;
}
for (int i = x - 1; i >= 0; i--) {
if (arr[y][i] == 1) check = true;
else if (arr[y][i] == 3) break;
}
for (int i = y + 1; i < 8; i++) {
if (arr[i][x] == 1) check = true;
else if (arr[i][x] == 3) break;
}
}
if (check) System.out.println(1);
else System.out.println(0);
}
}해설
체스판이 8*8이므로 이중 배열의 크기를 [8][8]로 잡는다.
그 후 룩의 개수가 2개일 수도 있으므로 , 룩의 각 x, y좌표를 저장할 배열을 선언한다.
값을 넣는다. 값을 넣을 때, 룩의 값을 저장할 때, x, y좌표를 넣는다.
이후 룩의 좌표에서 오른쪽, 왼쪽, 위, 아래로 이동하면서,
킹을 만나면, check를 true로 바꿔준다.
만약 3을 만나면, 즉 장애물을 만난다면 break를 한다.
룩의 수가 2개일 수도 있으므로, k값이 증가하면, 2번째 룩의 이동경로를 탐색한다.
개선점이나 오류가 있다면, 댓글 부탁드립니다.
'PS > 알고리즘 문제풀이' 카테고리의 다른 글
| *완전 탐색* attackRange (1) | 2022.09.15 |
|---|---|
| *완전탐색* colorpaper (0) | 2022.09.14 |
| [백준]1213번 팰린드롬 만들기(java) (0) | 2022.09.10 |
| *배열* arr3 (java, 알고리즘) (0) | 2022.09.04 |
| *다중 반복문* 숫자 피라미드(java, 알고리즘) (0) | 2022.09.04 |
