문제를 효율적으로 해결하는 것은 무엇일까?
똑같은 문제를 해결해도 빠르게 해결하는 것이 중요하다.
같은 입력을 제공했을 때, 어느 프로그램이 더 빠른가?
내 프로그램은 얼마나 빠를까?
라는 의문을 가지고 나오게 된 것이 시간 복잡도이다.
프로그램이 대략적으로 몇 개의 명령을 수행하는가?
public class Main {
public static void main(String[] args) {
int a =1, b= 5;
int sum = a+b;
System.out.println(sum);
}
}위와 같은 코드는 a, b를 선언하고 sum 에다 a+b 값을 넣어주고 출력해주는 코드이다.
위는 대략 3번이 실행되는 데 이것은 O(3)이라고 한다. O는 Big-O를 나타내고 읽을 때는 빅-오 또는 오더라고 읽는다.
우리 프로그램은 매우 빠르기 때문에 위와 같은 같은 O(3) = O(1)로 본다.
다음 예제를 보자.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int sum=0;
int n =sc.nextInt();
for (int i=0;i<n;i++){
sum+=i;
}
System.out.println(sum);
}
}위의 코드는 반복문이 추가되었다. n의 값에 따라 달라진다.
대략 O(n+4)인데, n이 절대적으로 영향을 끼치므로 뒤의 상수는 생략한다.
즉 위의 시간 복잡도는 O(n)을 갖게 된다.
다음 예제를 보자.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int sum=0;
int n =sc.nextInt();
for (int i=0;i<n;i++){
for (int j=0;j<n;j++){
sum+=i*j;
}
}
for (int i=0;i<n; i++){
sum+=i;
}
System.out.println(sum);
}
}위의 코드를 보면, 이중 for문과 for문이 들어가 있다.
우리는 시간 복잡도가 O(n^2 + n)이라는 것을 예상할 수 있다.
하지만 n^2은 n에 비해 엄청 큰 수이기 때문에 n은 생략하게 된다.
즉 위 코드의 시간 복자도는 O(n^2)이 된다.
다음 예제를 보자.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int sum=0;
int n =sc.nextInt();
for (int i=0;i<n;i++){
sum +=i;
if (i*i==n)break;
}
System.out.println(sum);
}
}위의 코드를 보면, n의 값에 따라 반복문의 횟수가 달라진다.
예를 들면 n이 9일 경우 반복문은 3번 반복하고 끝난다.
하지만 운이 좋지 않을 경우 n이 primeNumber이기 때문에 n까지 반복문을 수행하는 경우도 생기게 된다.
우리는 시간 복잡도를 계산할 때 항상 최악의 경우를 생각해야 한다.
따라서 위 코드의 시간 복잡도는 O(n)이 된다.
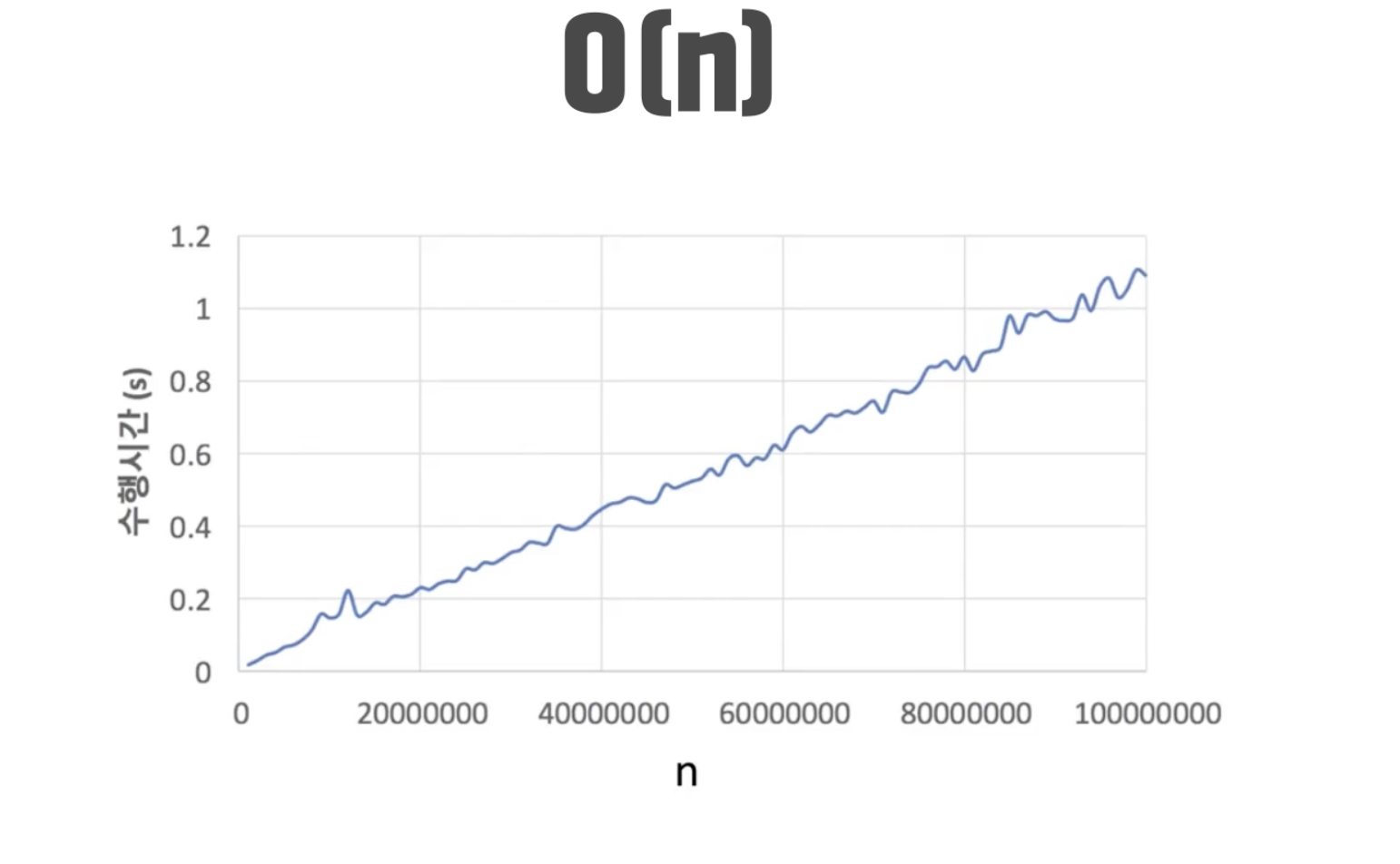
O(n)의 시간 복잡도가 실제 실행되는 시간이다.
직선을 예상했지만, 직선이 아닌 이유는 우리의 컴퓨터가 다른 작업을 실행할 수도 있고,
여러 가지 다른 변수들이 있기 때문에 일정하지 않다. 하지만 우리의 예상과 비슷한 결과를 얻게 된다.
우리가 알아두면 좋은 것은 대략 O(n)에서 n의 값이 1억이 되면 대략 1초가 걸린다는 것이다.
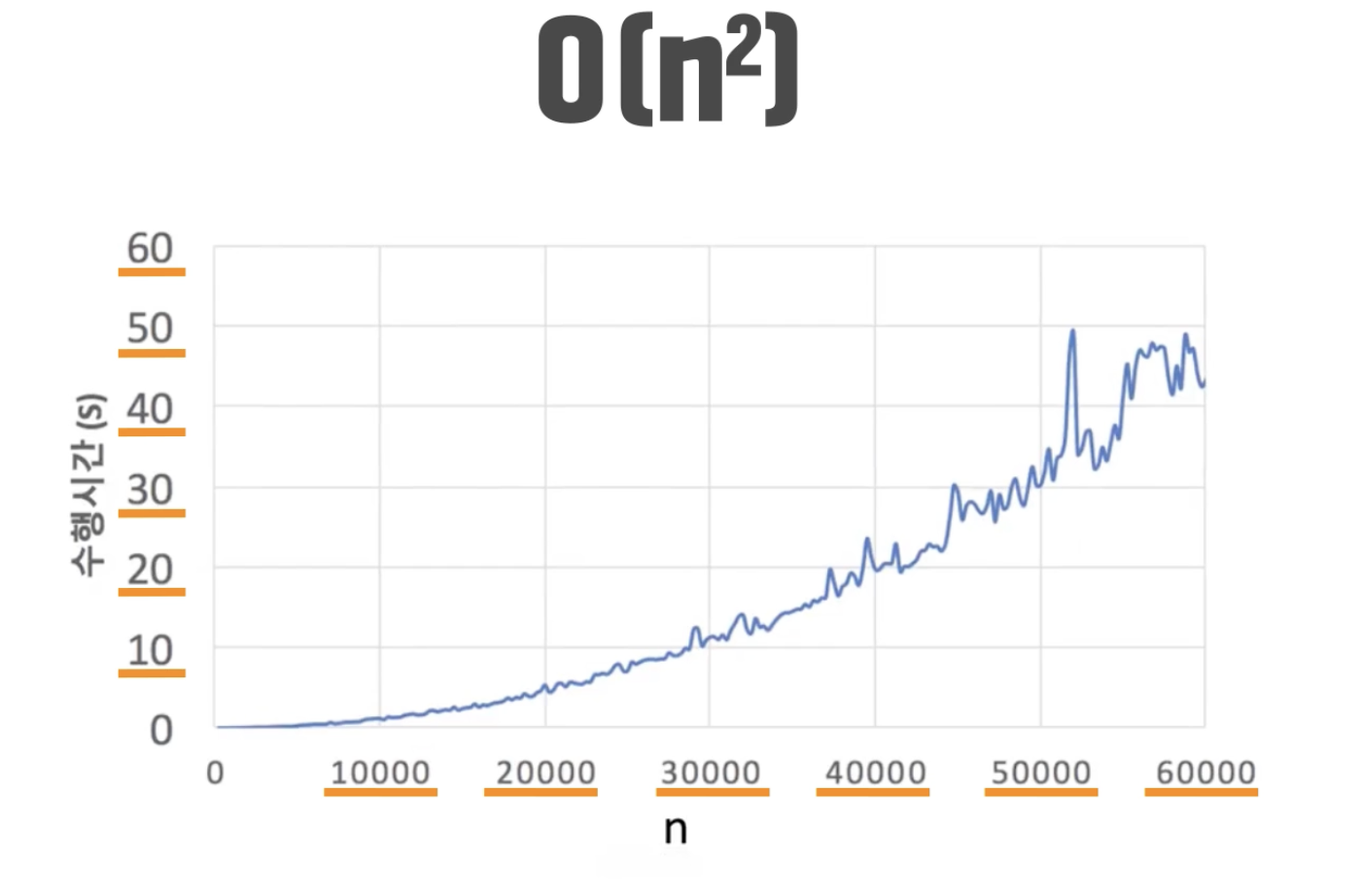
다음은 O(n^2)의 시간 복잡도이다.
위와 같은 이유로 그래프는 일정하지 않다.
위 그래프를 통해 우리가 알 수 있는 사실은 O(n^2)의 경우 n의 값이 점차 증가함에 따라 수행 시간이 매우 크게 증가한다.
그리고 중요하게 기억해둬야 할 부분은 O(n^2)의 시간 복잡도에서 n이 10000일 때 대략 1초가 걸린다.
문제를 효율적으로 해결하는 것은 무엇일까?
똑같은 문제를 해결해도 빠르게 해결하는 것이 중요하다.
같은 입력을 제공했을 때, 어느 프로그램이 더 빠른가?
내 프로그램은 얼마나 빠를까?
라는 의문을 가지고 나오게 된 것이 시간 복잡도이다.
프로그램이 대략적으로 몇 개의 명령을 수행하는가?
public class Main {
public static void main(String[] args) {
int a =1, b= 5;
int sum = a+b;
System.out.println(sum);
}
}위와 같은 코드는 a, b를 선언하고 sum 에다 a+b 값을 넣어주고 출력해주는 코드이다.
위는 대략 3번이 실행되는 데 이것은 O(3)이라고 한다. O는 Big-O를 나타내고 읽을 때는 빅-오 또는 오더라고 읽는다.
우리 프로그램은 매우 빠르기 때문에 위와 같은 같은 O(3) = O(1)로 본다.
다음 예제를 보자.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int sum=0;
int n =sc.nextInt();
for (int i=0;i<n;i++){
sum+=i;
}
System.out.println(sum);
}
}위의 코드는 반복문이 추가되었다. n의 값에 따라 달라진다.
대략 O(n+4)인데, n이 절대적으로 영향을 끼치므로 뒤의 상수는 생략한다.
즉 위의 시간 복잡도는 O(n)을 갖게 된다.
다음 예제를 보자.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int sum=0;
int n =sc.nextInt();
for (int i=0;i<n;i++){
for (int j=0;j<n;j++){
sum+=i*j;
}
}
for (int i=0;i<n; i++){
sum+=i;
}
System.out.println(sum);
}
}위의 코드를 보면, 이중 for문과 for문이 들어가 있다.
우리는 시간 복잡도가 O(n^2 + n)이라는 것을 예상할 수 있다.
하지만 n^2은 n에 비해 엄청 큰 수이기 때문에 n은 생략하게 된다.
즉 위 코드의 시간 복자도는 O(n^2)이 된다.
다음 예제를 보자.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int sum=0;
int n =sc.nextInt();
for (int i=0;i<n;i++){
sum +=i;
if (i*i==n)break;
}
System.out.println(sum);
}
}위의 코드를 보면, n의 값에 따라 반복문의 횟수가 달라진다.
예를 들면 n이 9일 경우 반복문은 3번 반복하고 끝난다.
하지만 운이 좋지 않을 경우 n이 primeNumber이기 때문에 n까지 반복문을 수행하는 경우도 생기게 된다.
우리는 시간 복잡도를 계산할 때 항상 최악의 경우를 생각해야 한다.
따라서 위 코드의 시간 복잡도는 O(n)이 된다.

O(n)의 시간 복잡도가 실제 실행되는 시간이다.
직선을 예상했지만, 직선이 아닌 이유는 우리의 컴퓨터가 다른 작업을 실행할 수도 있고,
여러 가지 다른 변수들이 있기 때문에 일정하지 않다. 하지만 우리의 예상과 비슷한 결과를 얻게 된다.
우리가 알아두면 좋은 것은 대략 O(n)에서 n의 값이 1억이 되면 대략 1초가 걸린다는 것이다.

다음은 O(n^2)의 시간 복잡도이다.
위와 같은 이유로 그래프는 일정하지 않다.
위 그래프를 통해 우리가 알 수 있는 사실은 O(n^2)의 경우 n의 값이 점차 증가함에 따라 수행 시간이 매우 크게 증가한다.
그리고 중요하게 기억해둬야 할 부분은 O(n^2)의 시간 복잡도에서 n이 10000일 때 대략 1초가 걸린다.
