자료구조에서 트리는 다음과 같은 모습을 가진다.
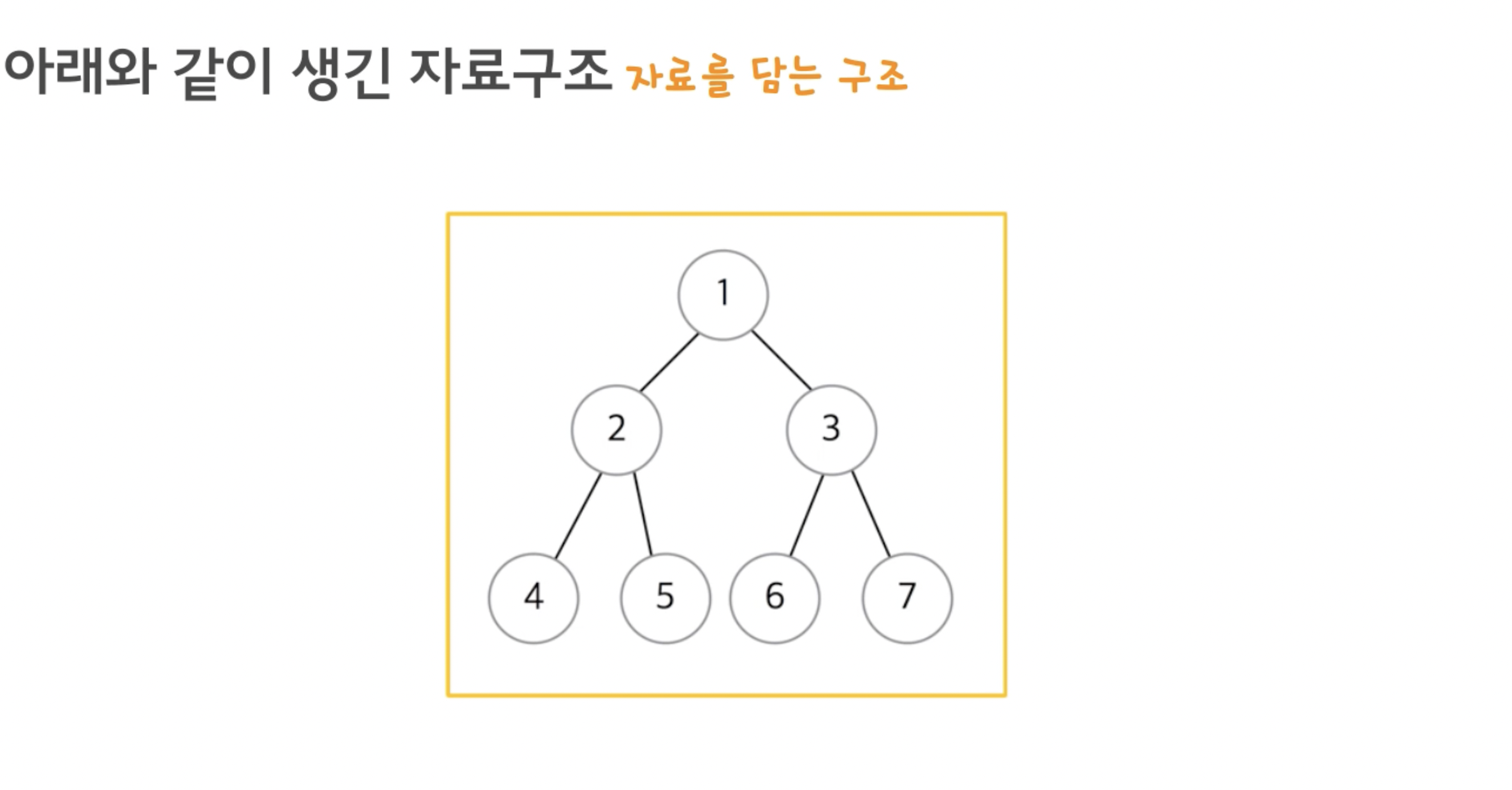
아마 위의 사진만 보고도 대충 짐작을 할 수 있을 것이다.
트리는 자식 노드와 부모 노드로 이루어져 있다.
자식 노드에서 부모 쪽으로 계속해서 타고 올라가다 보면 결국 부모가 없는 하나의 노드로 이어지게 되는데,
이 노드를 루트 노드라고 부르며, 루트 노드를 중심으로 뻗어나가는 모습이 나무의 구조와 비슷하여 '트리'라는 이름이 붙여졌다.
트리의 재귀적 성질
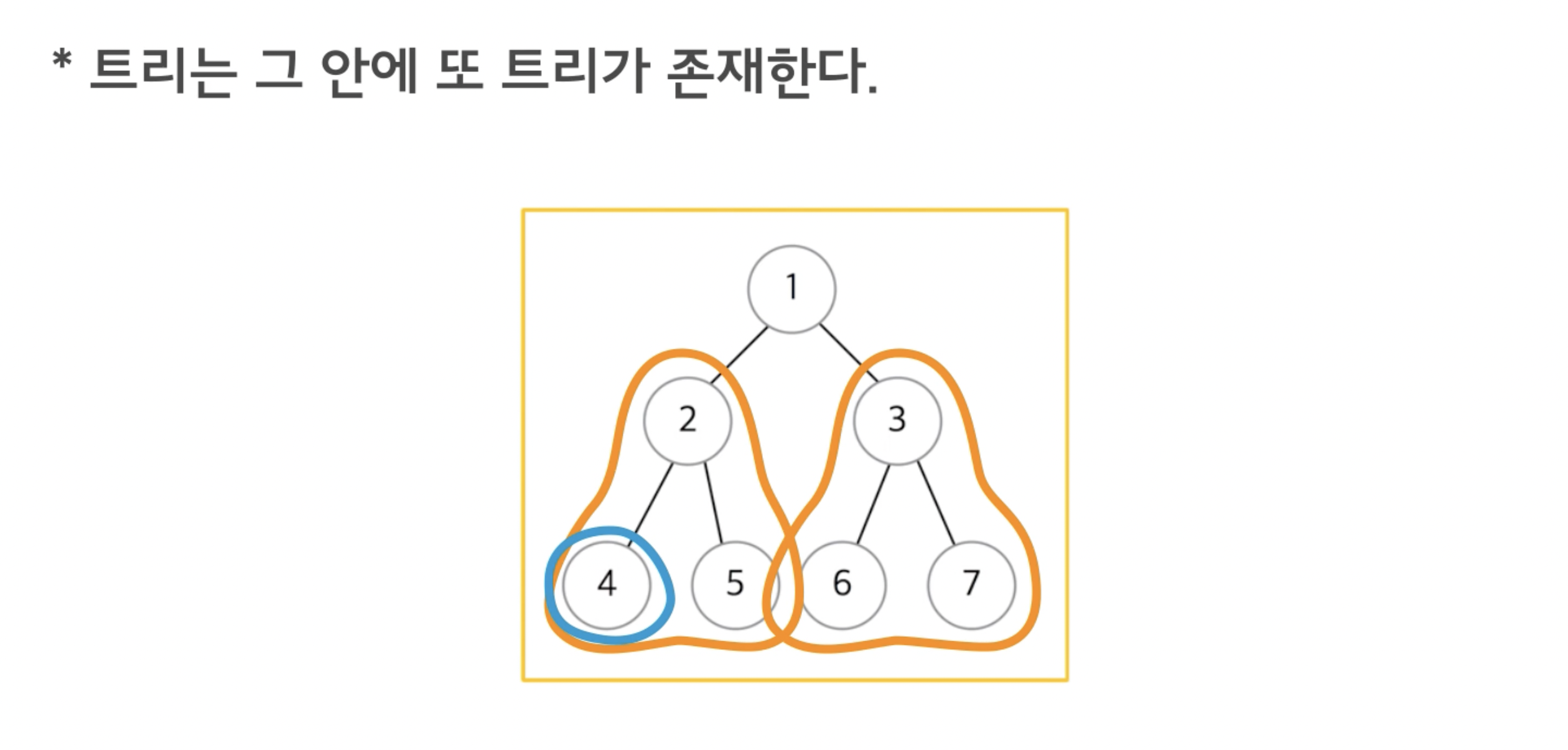
트리는 그 안에 또 트리가 존재하게 된다. 트리안의 다른 트리를 서브 트리라고 한다.
이진트리(Binary Tree)
이름에서도 알 수 있듯이 자식 노드가 2개 이하인 트리를 이진트리라고 한다.
트리 순회
트래 내에 어떠한 자료가 담겨있는지를 알기 위해 사용한다.
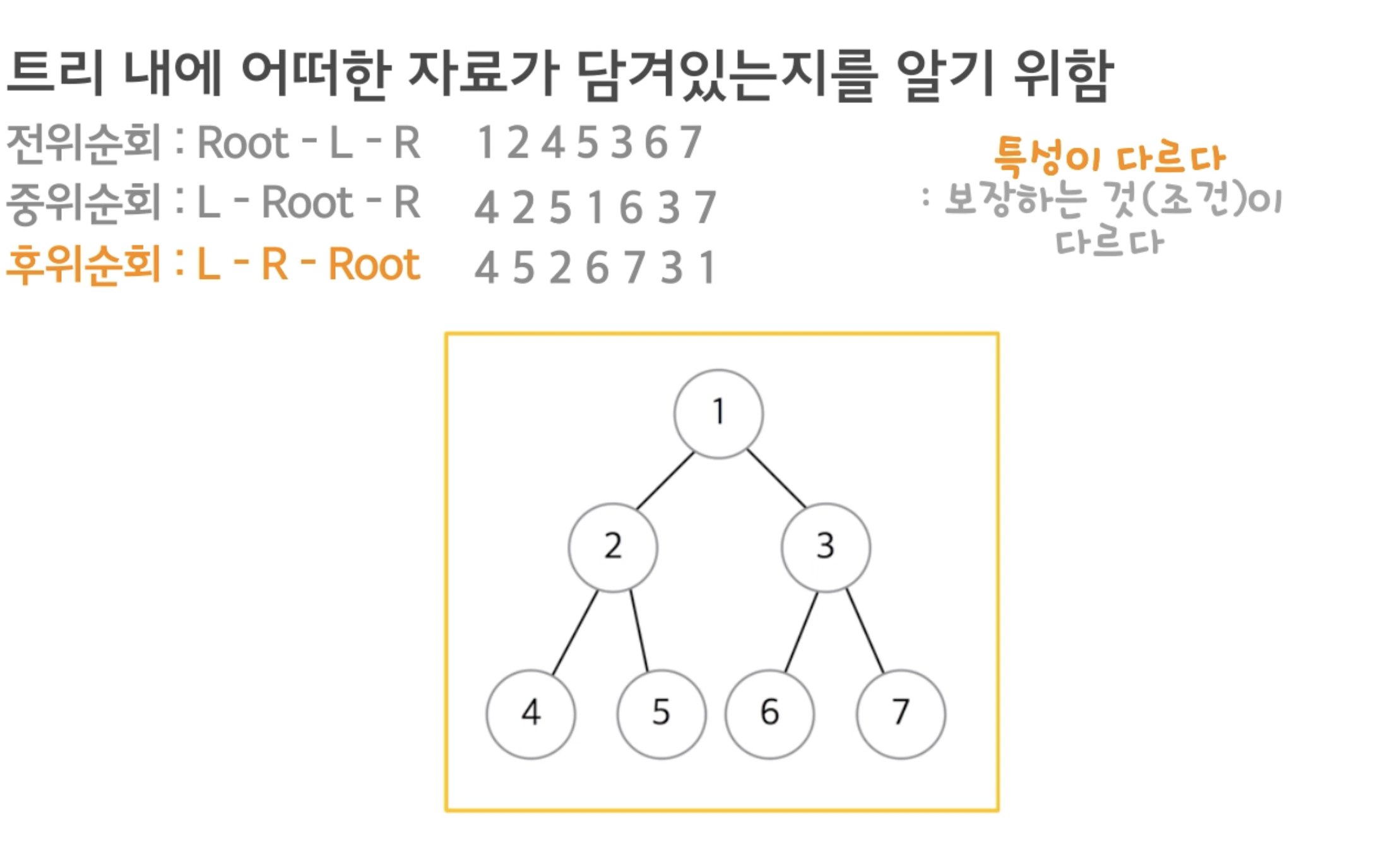
- 전위 순회: Root - Left - Right
- 중위 순회: Left - Root - Right
- 후위 순회: Left - Right - Root
트리의 순회 구현하기
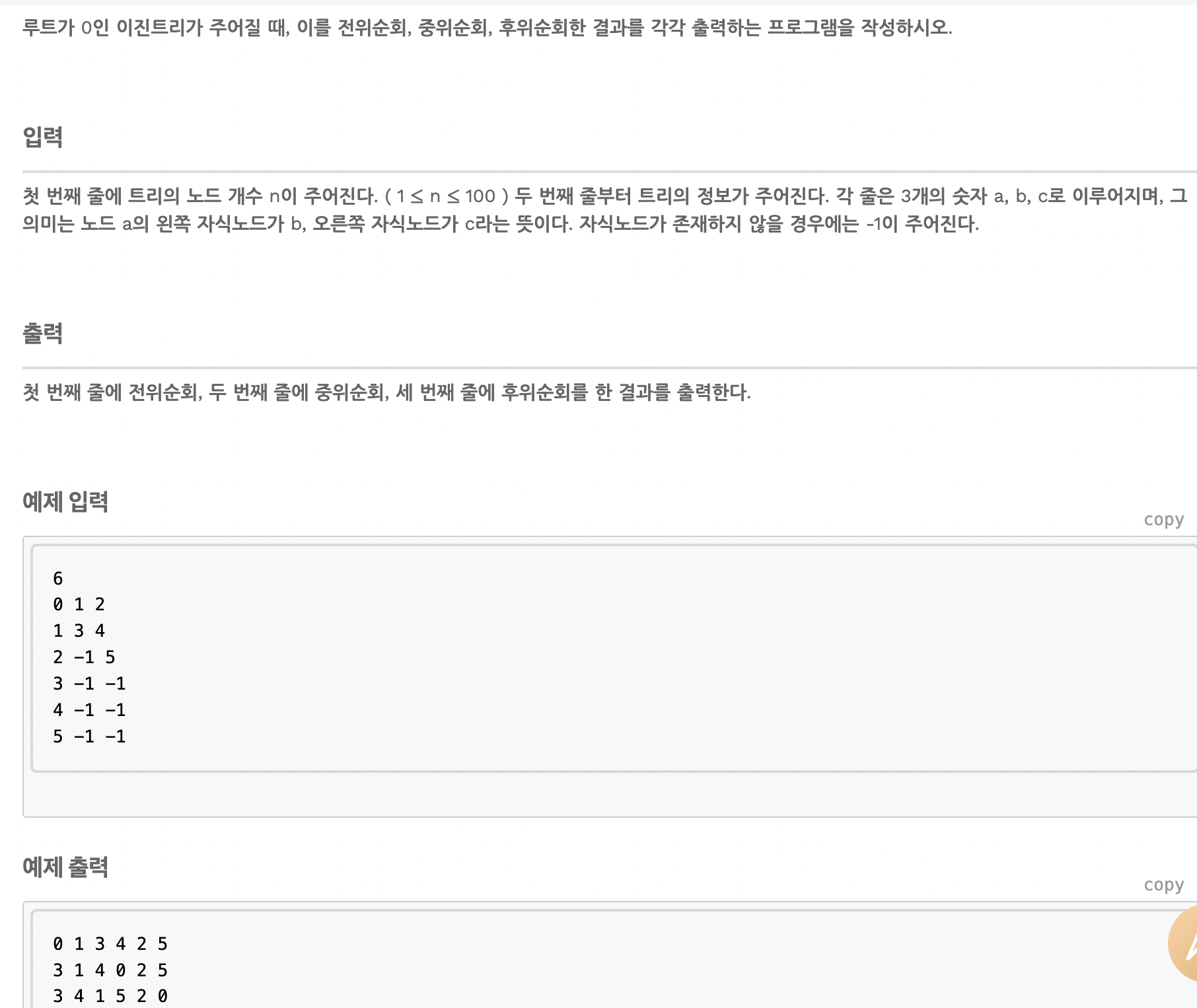
정답 코드
import java.util.Scanner;
public class Main {
private static int[][] tree;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
tree = new int[n][2];
for (int i = 0; i < n; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
tree[a][0] = b;
tree[a][1] = c;
}
preOrder(0);
System.out.println();
inOrder(0);
System.out.println();
postOrder(0);
}
//전위 root - left - right
private static void preOrder(int root) {
if (tree[root][0] == -1 && tree[root][1] == -1) System.out.print(root + " ");
else {
System.out.print(root + " ");
if (tree[root][0] != -1) preOrder(tree[root][0]);
if (tree[root][1] != -1) preOrder(tree[root][1]);
}
}
//중위 left - root - right
private static void inOrder(int root) {
if (tree[root][0] == -1 && tree[root][1] == -1) System.out.print(root + " ");
else {
if (tree[root][0] != -1) inOrder(tree[root][0]);
System.out.print(root + " ");
if (tree[root][1] != -1) inOrder(tree[root][1]);
}
}
//후위 left - right - root
private static void postOrder(int root) {
if (tree[root][0] == -1 && tree[root][1] == -1) System.out.print(root + " ");
else {
if (tree[root][0] != -1) postOrder(tree[root][0]);
if (tree[root][1] != -1) postOrder(tree[root][1]);
System.out.print(root + " ");
}
}
}위 코드에서 중요한 부분은 preOrder, inOrder, postOrder메서드이다.
코드에서 알 수 있듯이 자식 노드가 없다면 root를 출력하고, else문을 실행한다.
전위, 중위, 후위 순회 코드에서 차이점은 root를 출력하는 차례이다. 이 부분을 잘 보면 쉽게 이해할 수 있다.
공통 조상 찾기
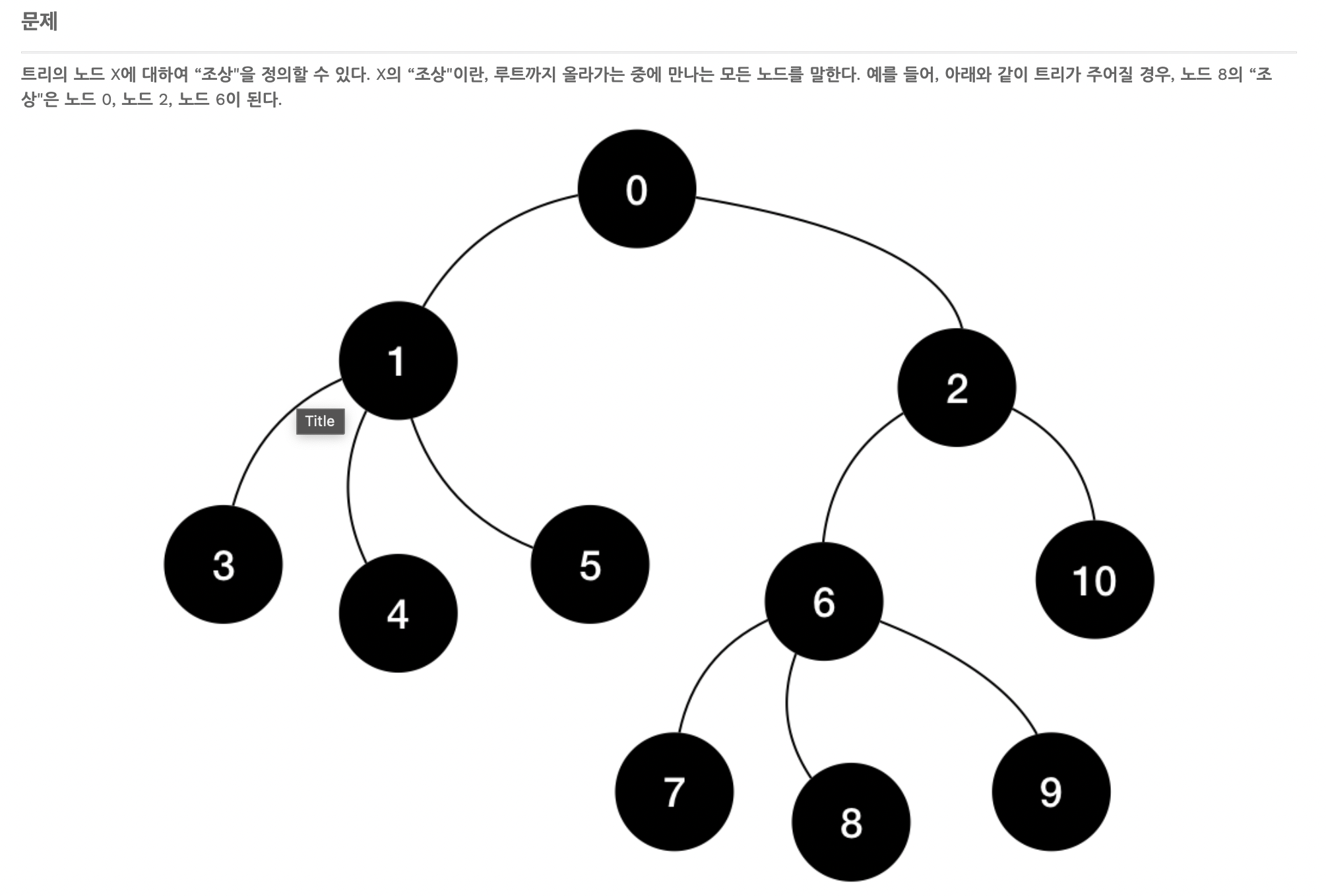
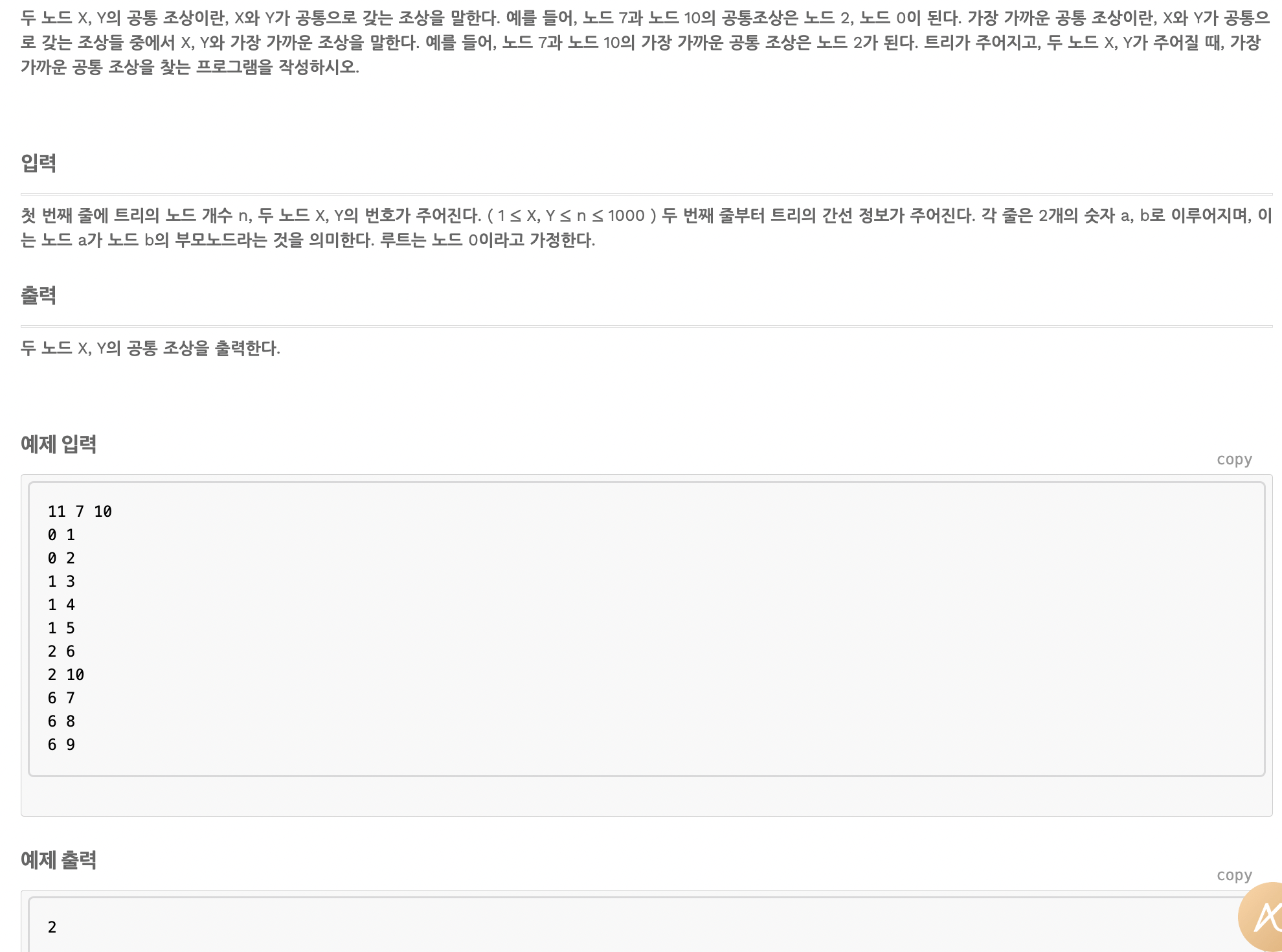
두 숫자를 선택하여, 가장 가까운 조상을 찾는 문제이다.
정답 코드
import java.util.Scanner;
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n =sc.nextInt();
int X = sc.nextInt();
int Y = sc.nextInt();
boolean[] check = new boolean[n];
int[] parent = new int[n];
for (int i=0;i<n-1;i++){
int a = sc.nextInt();
int b = sc.nextInt();
parent[b] = a;
}
while (true){
check[X] = true;
if (X==0) break;
X =parent[X];
}
while (true){
if (check[Y]){
System.out.println(Y);
return;
}
check[Y] = true;
Y = parent[Y];
}
}
}이 문제에서 핵심은 boolean배열을 사용하는 것이다. 우리가 원하는 2개의 숫자 중에서, 첫 번째 수의 조상을 모두 true로 바꾼다.
그 후 두 번째 수의 조상을 true로 바꾸면서 가장 먼저 만나는 조상이 가장 가까운 공통 조상이다.
트리에서의 거리
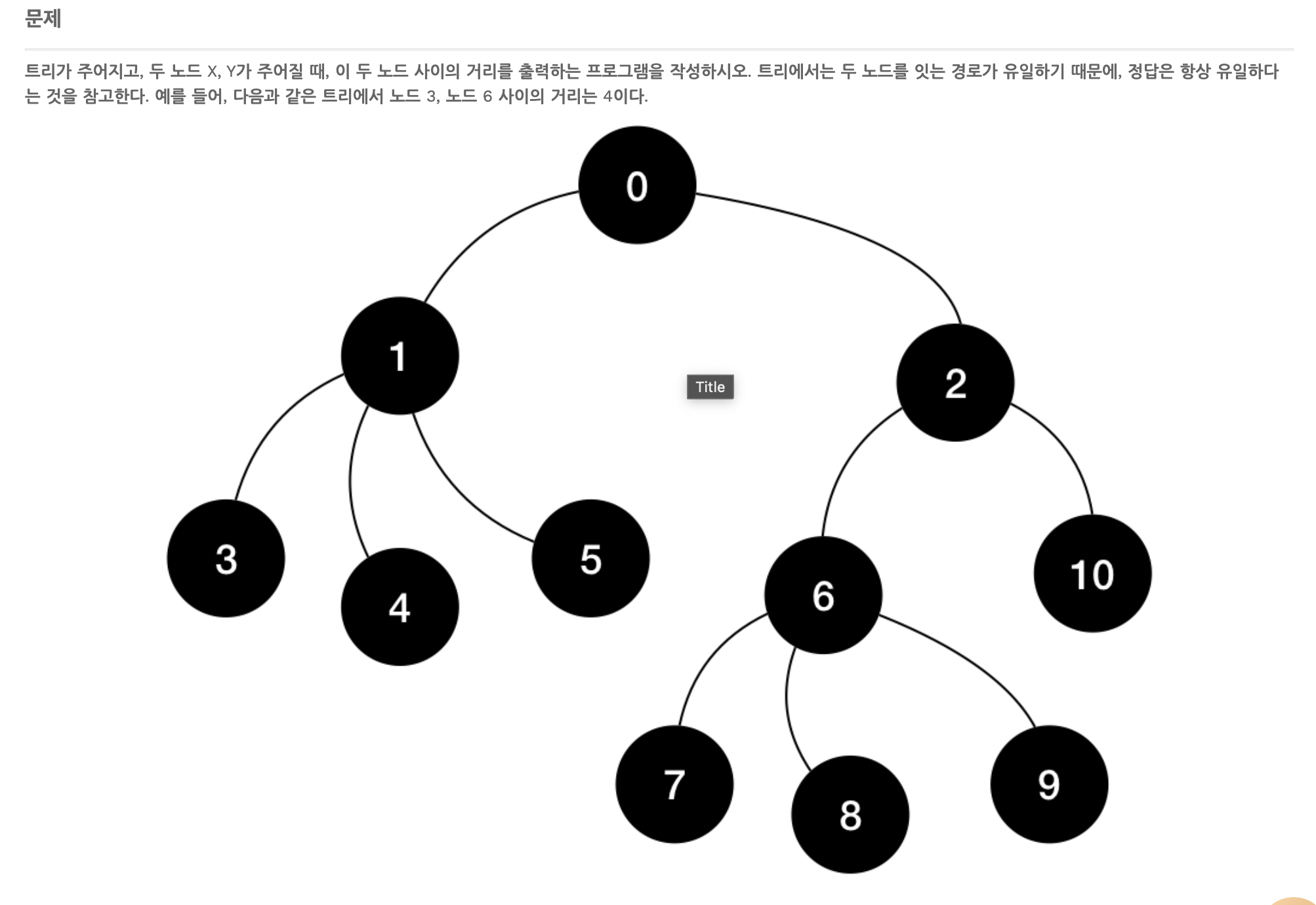
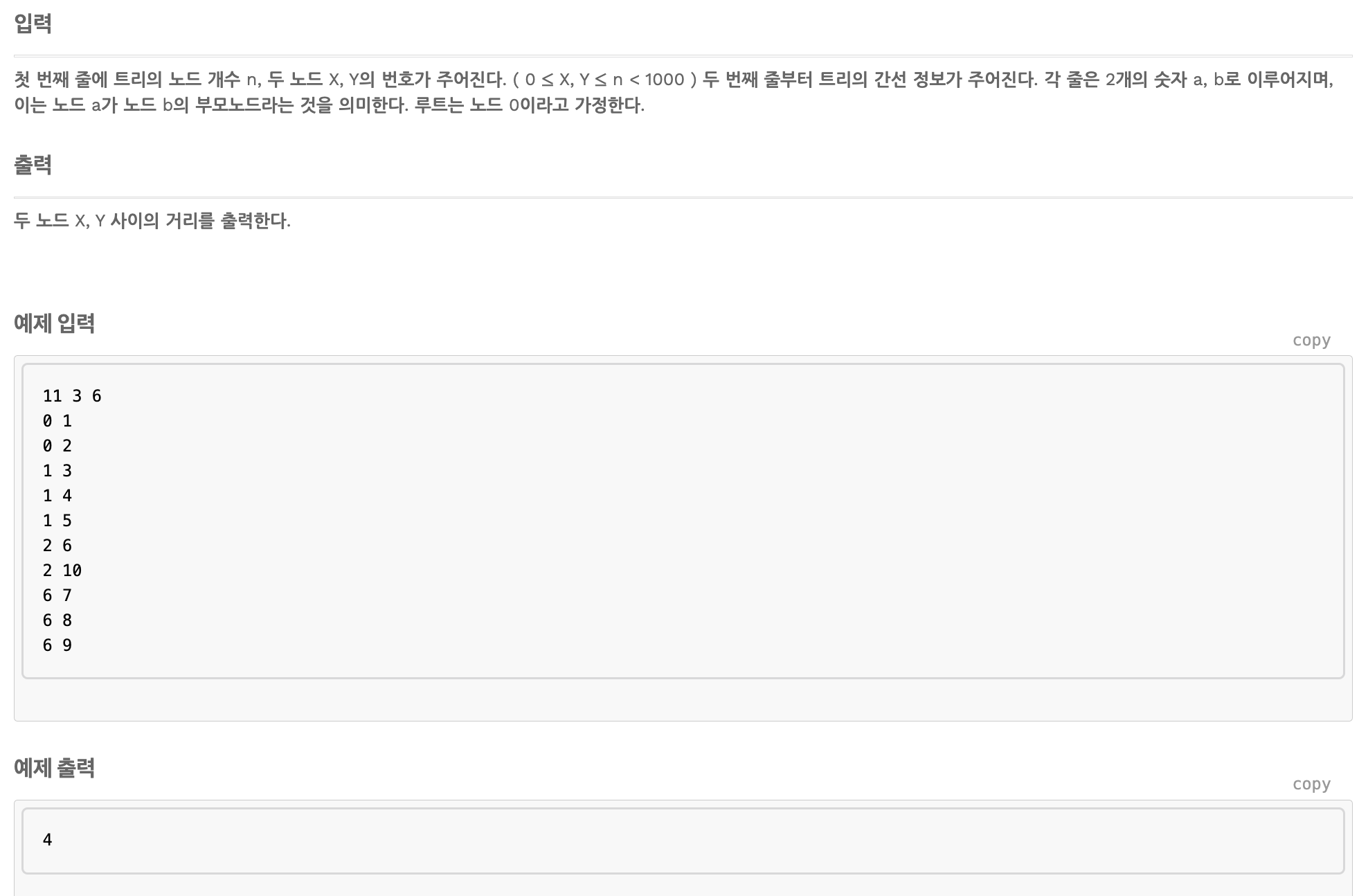
이 문제는 조상 찾기의 문제에서 응용된 문제이다. 두 노드의 거리를 찾는 것이다.
정답 코드
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int X = sc.nextInt();
int Y = sc.nextInt();
int[] parent = new int[n];
boolean[] check = new boolean[n];
for (int i=0;i<n-1;i++){
int a = sc.nextInt();
int b = sc.nextInt();
parent[b] = a;
}
int Xcount=0;
while (true){
check[X] = true;
if (X==0)break;
X = parent[X];
Xcount++;
}
int Ycount = 0;
while (true){
if (check[Y])break;
check[Y] =true;
Y = parent[Y];
Ycount++;
}
System.out.println(Ycount+Xcount);
}
}우리가 알아야 할 것은 어떤 노드라도 결국에 맨 위의 조상은 같다는 것이다.
위의 문제와 매우 유사하게 풀 수 있다.
x와 y의 조상을 만날 때까지 카운트를 센 다음, 그 카운트를 더하면 쉽게 풀 수 있다.
트리의 높이
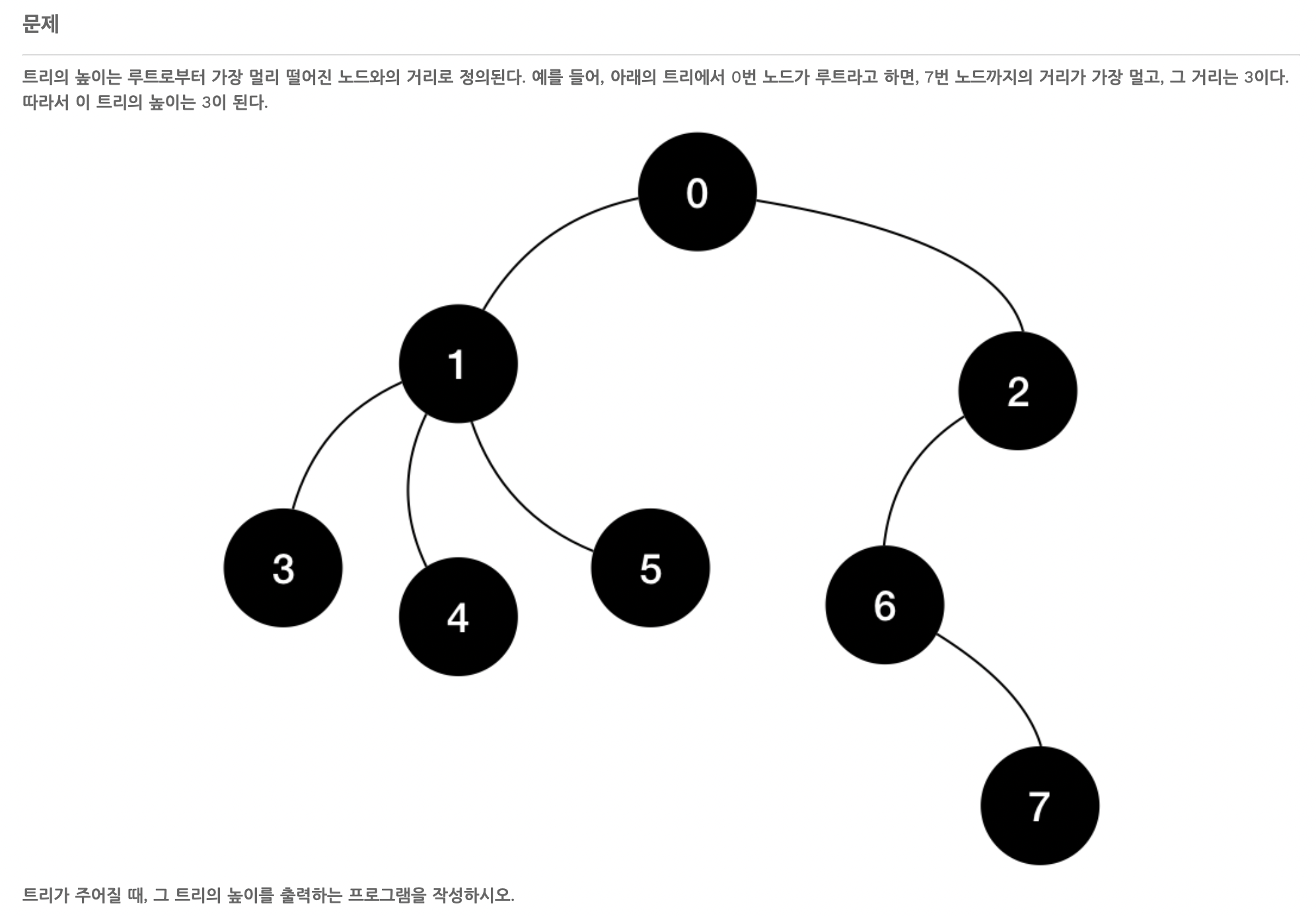
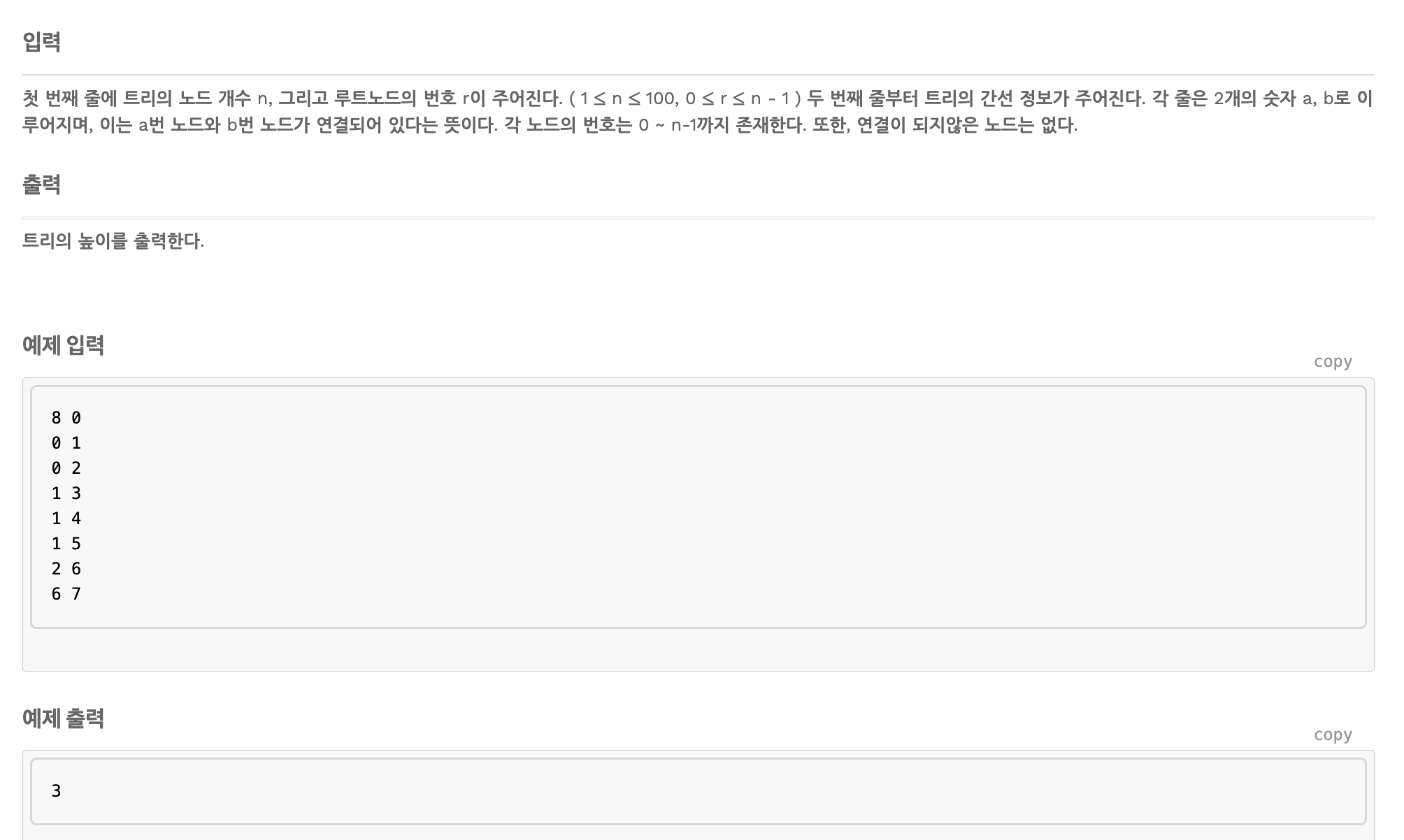
이 문제도 위의 문제들에서 응용된 문제이다.
정답 코드
import java.util.Scanner;
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int r = sc.nextInt();
int[] parent = new int[n];
for (int i =0;i<n-1;i++){
int a = sc.nextInt();
int b = sc.nextInt();
parent[b]=a;
}
int high = 0;
for (int i = 0;i<n-1;i++){
int count =0;
int j =i;
while (true){
count++;
if (j==r)break;
j=parent[j];
}
high = Math.max(high,count);
}
System.out.println(high);
}
}이 문제도 쉽게 풀 수 있다. 각 숫자에서 들을 루트 노드까지 가는데 걸리는 count를 배열에 저장한다.
이후 그 배열에서 최댓값을 출력하면 된다.
배운 점
트리를 이번에 공부하면서 자세히 알게 된 것 같다.
이미 구현되어 있는 자료구조를 사용만 하는 것보다는 직접 구현해보는 것이 이해하는데 큰 도움이 되는 것 같다.
'PS > 알고리즘' 카테고리의 다른 글
| 깊이 우선 탐색(DFS) (2) | 2022.11.06 |
|---|---|
| 자료구조(Graph) (2) | 2022.11.02 |
| 자료구조(Stack&Queue) (0) | 2022.10.26 |
| 이진탐색 (0) | 2022.10.21 |
| 재귀함수 (1) | 2022.10.18 |
자료구조에서 트리는 다음과 같은 모습을 가진다.

아마 위의 사진만 보고도 대충 짐작을 할 수 있을 것이다.
트리는 자식 노드와 부모 노드로 이루어져 있다.
자식 노드에서 부모 쪽으로 계속해서 타고 올라가다 보면 결국 부모가 없는 하나의 노드로 이어지게 되는데,
이 노드를 루트 노드라고 부르며, 루트 노드를 중심으로 뻗어나가는 모습이 나무의 구조와 비슷하여 '트리'라는 이름이 붙여졌다.
트리의 재귀적 성질

트리는 그 안에 또 트리가 존재하게 된다. 트리안의 다른 트리를 서브 트리라고 한다.
이진트리(Binary Tree)
이름에서도 알 수 있듯이 자식 노드가 2개 이하인 트리를 이진트리라고 한다.
트리 순회
트래 내에 어떠한 자료가 담겨있는지를 알기 위해 사용한다.

- 전위 순회: Root - Left - Right
- 중위 순회: Left - Root - Right
- 후위 순회: Left - Right - Root
트리의 순회 구현하기

정답 코드
import java.util.Scanner;
public class Main {
private static int[][] tree;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
tree = new int[n][2];
for (int i = 0; i < n; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
tree[a][0] = b;
tree[a][1] = c;
}
preOrder(0);
System.out.println();
inOrder(0);
System.out.println();
postOrder(0);
}
//전위 root - left - right
private static void preOrder(int root) {
if (tree[root][0] == -1 && tree[root][1] == -1) System.out.print(root + " ");
else {
System.out.print(root + " ");
if (tree[root][0] != -1) preOrder(tree[root][0]);
if (tree[root][1] != -1) preOrder(tree[root][1]);
}
}
//중위 left - root - right
private static void inOrder(int root) {
if (tree[root][0] == -1 && tree[root][1] == -1) System.out.print(root + " ");
else {
if (tree[root][0] != -1) inOrder(tree[root][0]);
System.out.print(root + " ");
if (tree[root][1] != -1) inOrder(tree[root][1]);
}
}
//후위 left - right - root
private static void postOrder(int root) {
if (tree[root][0] == -1 && tree[root][1] == -1) System.out.print(root + " ");
else {
if (tree[root][0] != -1) postOrder(tree[root][0]);
if (tree[root][1] != -1) postOrder(tree[root][1]);
System.out.print(root + " ");
}
}
}위 코드에서 중요한 부분은 preOrder, inOrder, postOrder메서드이다.
코드에서 알 수 있듯이 자식 노드가 없다면 root를 출력하고, else문을 실행한다.
전위, 중위, 후위 순회 코드에서 차이점은 root를 출력하는 차례이다. 이 부분을 잘 보면 쉽게 이해할 수 있다.
공통 조상 찾기


두 숫자를 선택하여, 가장 가까운 조상을 찾는 문제이다.
정답 코드
import java.util.Scanner;
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n =sc.nextInt();
int X = sc.nextInt();
int Y = sc.nextInt();
boolean[] check = new boolean[n];
int[] parent = new int[n];
for (int i=0;i<n-1;i++){
int a = sc.nextInt();
int b = sc.nextInt();
parent[b] = a;
}
while (true){
check[X] = true;
if (X==0) break;
X =parent[X];
}
while (true){
if (check[Y]){
System.out.println(Y);
return;
}
check[Y] = true;
Y = parent[Y];
}
}
}이 문제에서 핵심은 boolean배열을 사용하는 것이다. 우리가 원하는 2개의 숫자 중에서, 첫 번째 수의 조상을 모두 true로 바꾼다.
그 후 두 번째 수의 조상을 true로 바꾸면서 가장 먼저 만나는 조상이 가장 가까운 공통 조상이다.
트리에서의 거리


이 문제는 조상 찾기의 문제에서 응용된 문제이다. 두 노드의 거리를 찾는 것이다.
정답 코드
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int X = sc.nextInt();
int Y = sc.nextInt();
int[] parent = new int[n];
boolean[] check = new boolean[n];
for (int i=0;i<n-1;i++){
int a = sc.nextInt();
int b = sc.nextInt();
parent[b] = a;
}
int Xcount=0;
while (true){
check[X] = true;
if (X==0)break;
X = parent[X];
Xcount++;
}
int Ycount = 0;
while (true){
if (check[Y])break;
check[Y] =true;
Y = parent[Y];
Ycount++;
}
System.out.println(Ycount+Xcount);
}
}우리가 알아야 할 것은 어떤 노드라도 결국에 맨 위의 조상은 같다는 것이다.
위의 문제와 매우 유사하게 풀 수 있다.
x와 y의 조상을 만날 때까지 카운트를 센 다음, 그 카운트를 더하면 쉽게 풀 수 있다.
트리의 높이


이 문제도 위의 문제들에서 응용된 문제이다.
정답 코드
import java.util.Scanner;
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int r = sc.nextInt();
int[] parent = new int[n];
for (int i =0;i<n-1;i++){
int a = sc.nextInt();
int b = sc.nextInt();
parent[b]=a;
}
int high = 0;
for (int i = 0;i<n-1;i++){
int count =0;
int j =i;
while (true){
count++;
if (j==r)break;
j=parent[j];
}
high = Math.max(high,count);
}
System.out.println(high);
}
}이 문제도 쉽게 풀 수 있다. 각 숫자에서 들을 루트 노드까지 가는데 걸리는 count를 배열에 저장한다.
이후 그 배열에서 최댓값을 출력하면 된다.
배운 점
트리를 이번에 공부하면서 자세히 알게 된 것 같다.
이미 구현되어 있는 자료구조를 사용만 하는 것보다는 직접 구현해보는 것이 이해하는데 큰 도움이 되는 것 같다.
'PS > 알고리즘' 카테고리의 다른 글
| 깊이 우선 탐색(DFS) (2) | 2022.11.06 |
|---|---|
| 자료구조(Graph) (2) | 2022.11.02 |
| 자료구조(Stack&Queue) (0) | 2022.10.26 |
| 이진탐색 (0) | 2022.10.21 |
| 재귀함수 (1) | 2022.10.18 |
