그래프 순회
- 그래프라는 자료구조에 어떠한 값이 저장되어 있는가?
깊이 우선 탐색(Depth First Search)
스택을 이용하여 그래프를 순회하는 방법
스택 = 선행 관계
- 나를 먼저 방문하고 그다음으로 인접한 노드를 차례로 방문(단, 방문했던 노드는 방문하지 않는다.)
깊이 우선 탐색의 예시
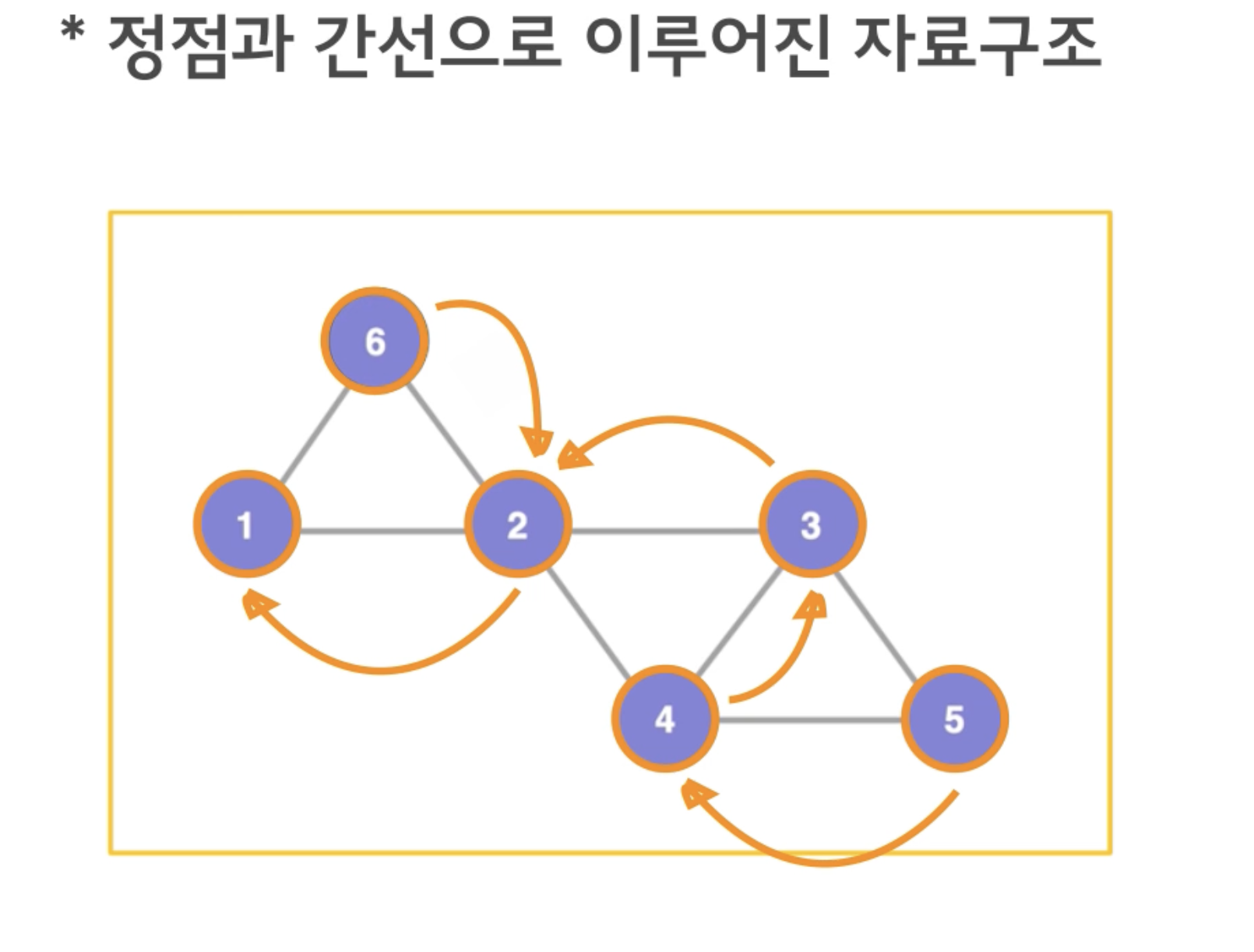
위 그래프는 1 - 2 - 3 - 4 - 5 - 6 순으로 방문하게 된다.
중요한 점은 더 이상 갈 곳이 없다면, 왔던 곳으로 돌아간다.(재귀)
좀 더 복잡해 보이는 그래프를 보자.
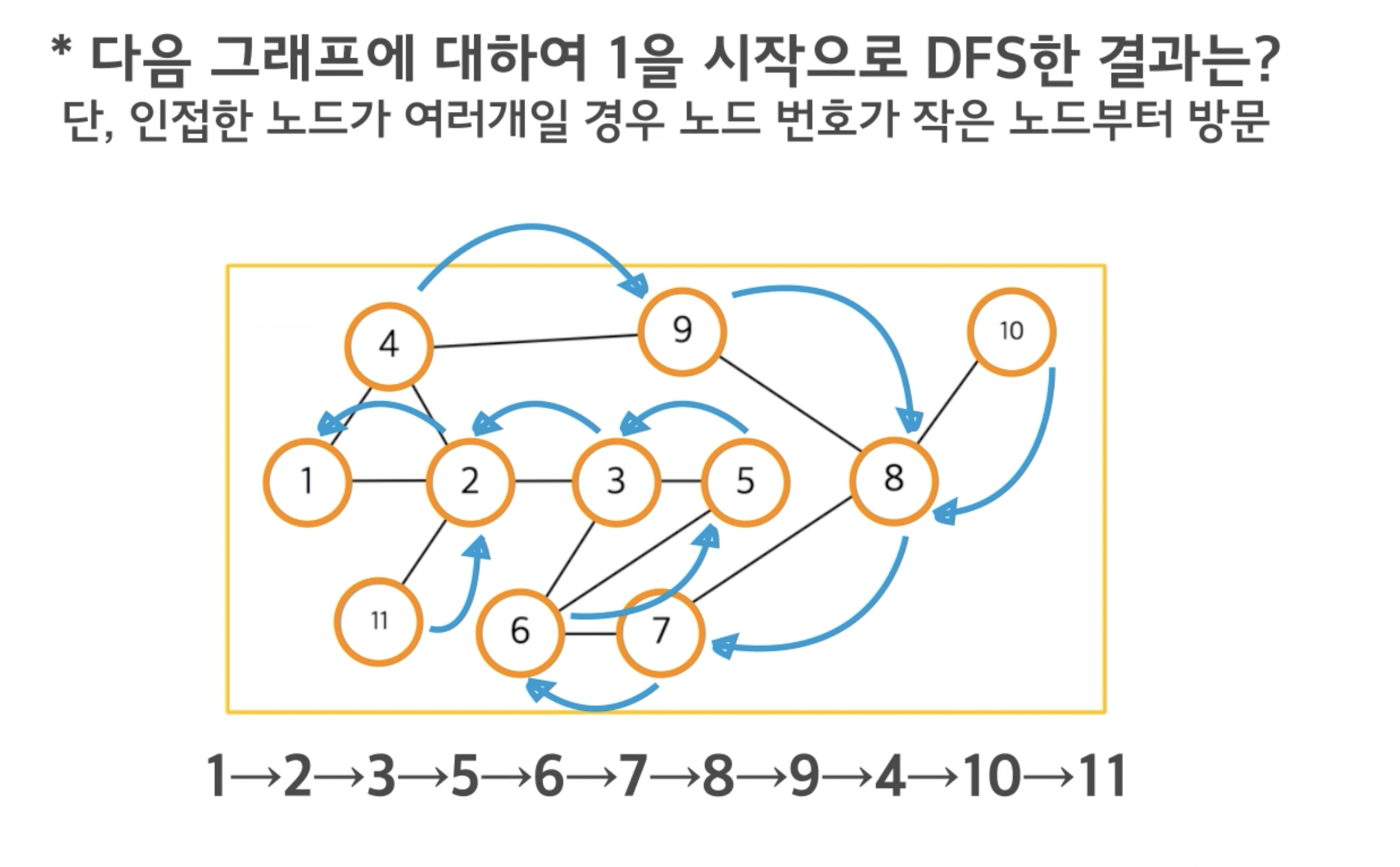
위에 보이는 순서대로 방문하게 되고, 화살표의 모양대로 다시 돌아오게 된다.
가장 깊은 4까지 간 뒤 더 이상 갈 곳이 없기 때문에 돌아오면서 방문하지 못한 곳을 방문하게 된다.
DFS 구현
DFS를 구현하고, 코드를 보며 자세하게 알아보자.
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
static List<Integer>[] graph;
static boolean[] visited;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int Node = sc.nextInt();
int Edge = sc.nextInt();
visited = new boolean[Node+1];
graph = new ArrayList[Node+1];
for (int i = 1; i <=Node; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < Edge; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
}
DFS(1);
}
//x부터 DFS시작
static void DFS(int x) {
visited[x] = true;
System.out.printf("%d ",x);
for (int i=0;i<graph[x].size();i++){
int y = graph[x].get(i);
if (visited[y]==false){
DFS(y);
}
}
}
}인접 배열과 인접 리스트 중 한 가지를 선택하여 구현할 수 있는데, 이번 구현은 인접 리스트를 사용하였다.
우리가 볼 부분은 DFS 메서드이다.
이미 방문한 곳은 재 방문하지 않기 위해 visted [x]를 true로 선언한다.
그리고 그때 값을 출력해준다.
for문에서 graph는 인접 리스트를 사용하였으므로, 인접한 노드들이 담겨있다.
따라서 y는 인접한 노드 중 숫자가 작은 값부터 DFS로 들어가게 된다.
DFS의 정확성 / 시간 복잡도
DFS가 정말 순회를 하는가?
모든 정점을 방문한다. 하나의 정점을 두 번 이상 방문하지 않는다.
자신을 방문하고, 모든 이웃에게 물어봄 -> |V| = 2*|E|
각 정점은 1번씩, 각 간선은 2번씩 방문한다.
따라서 O(V+E)의 시간 복잡도를 갖게 된다.
DFS 활용 문제를 풀어보자
웜 바이러스
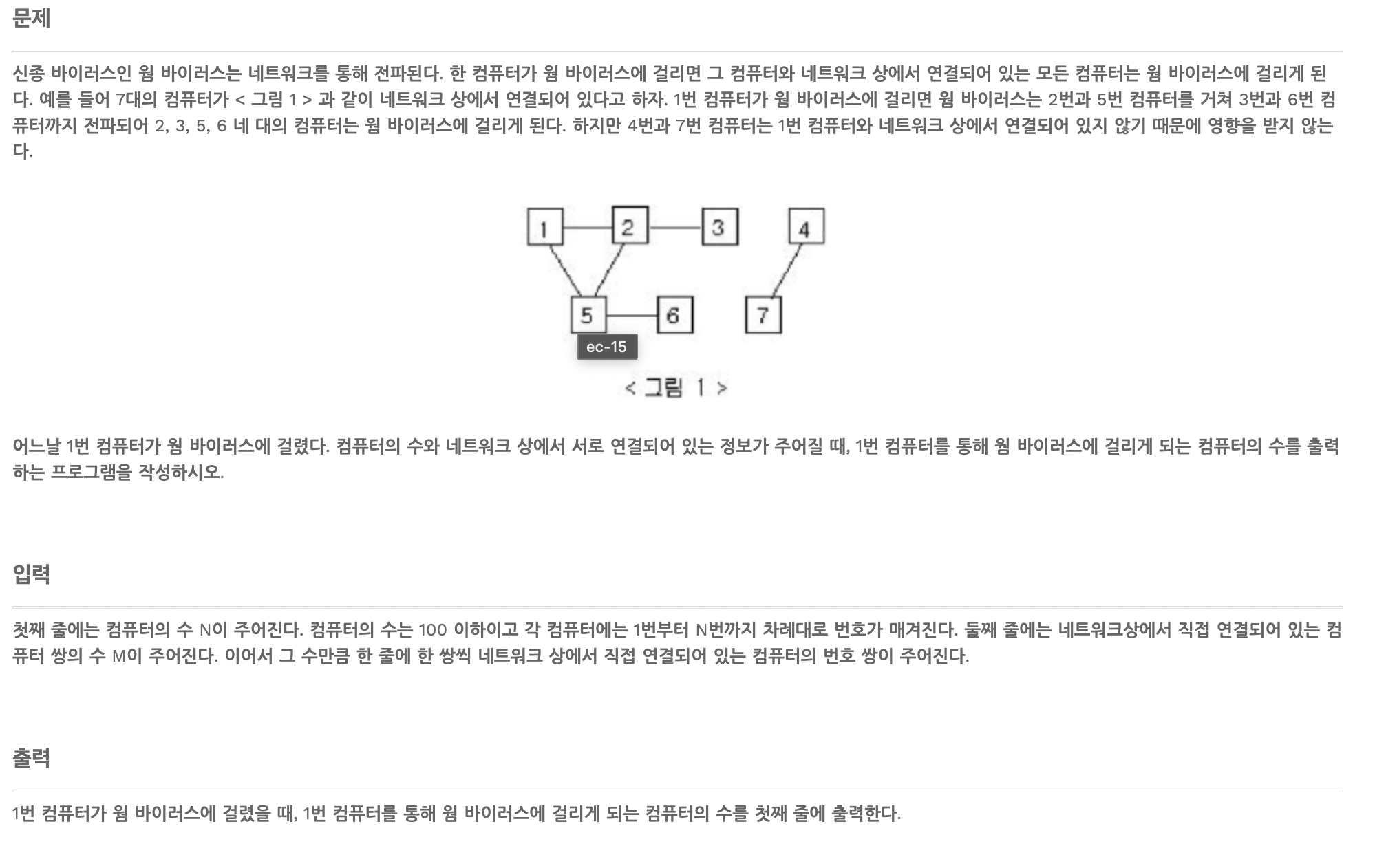
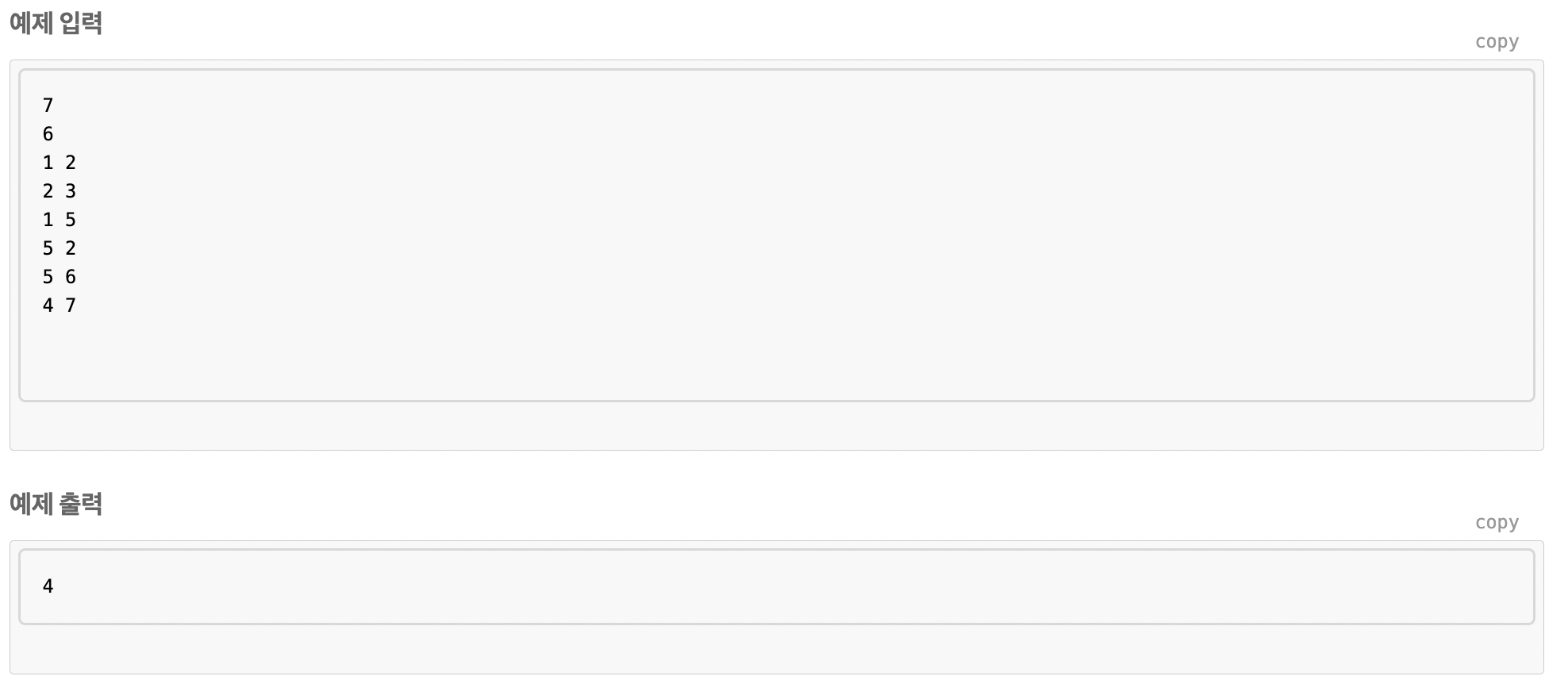
DFS를 이용하여 전부 탐색하고, 그 횟수를 찾으면 된다.
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main{
static List<Integer>[] graph;
static boolean[] visited;
static int count=-1;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int node = sc.nextInt();
int edge = sc.nextInt();
graph = new List[node+1];
visited = new boolean[node+1];
for (int i=1; i<=node;i++){
graph[i] = new ArrayList<>();
}
for (int i = 0;i<edge;i++){
int a = sc.nextInt();
int b = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
}
DFS(1);
System.out.println(count);
}
static void DFS(int x){
visited[x] = true;
count++;
for (int i=0;i<graph[x].size();i++){
int y = graph[x].get(i);
if (visited[y]==false){
DFS(y);
}
}
}
}우리가 구현한 DFS와 거의 흡사하다.
우리가 중요한 것은 총 방문한 노드의 수이므로 방문을 할 때마다 count를 증가시킨다.
여기서 중요한 점은 본인을 방문한 경우는 삐야 하므로 count = -1에서 시작한다.
이분 그래프 판별
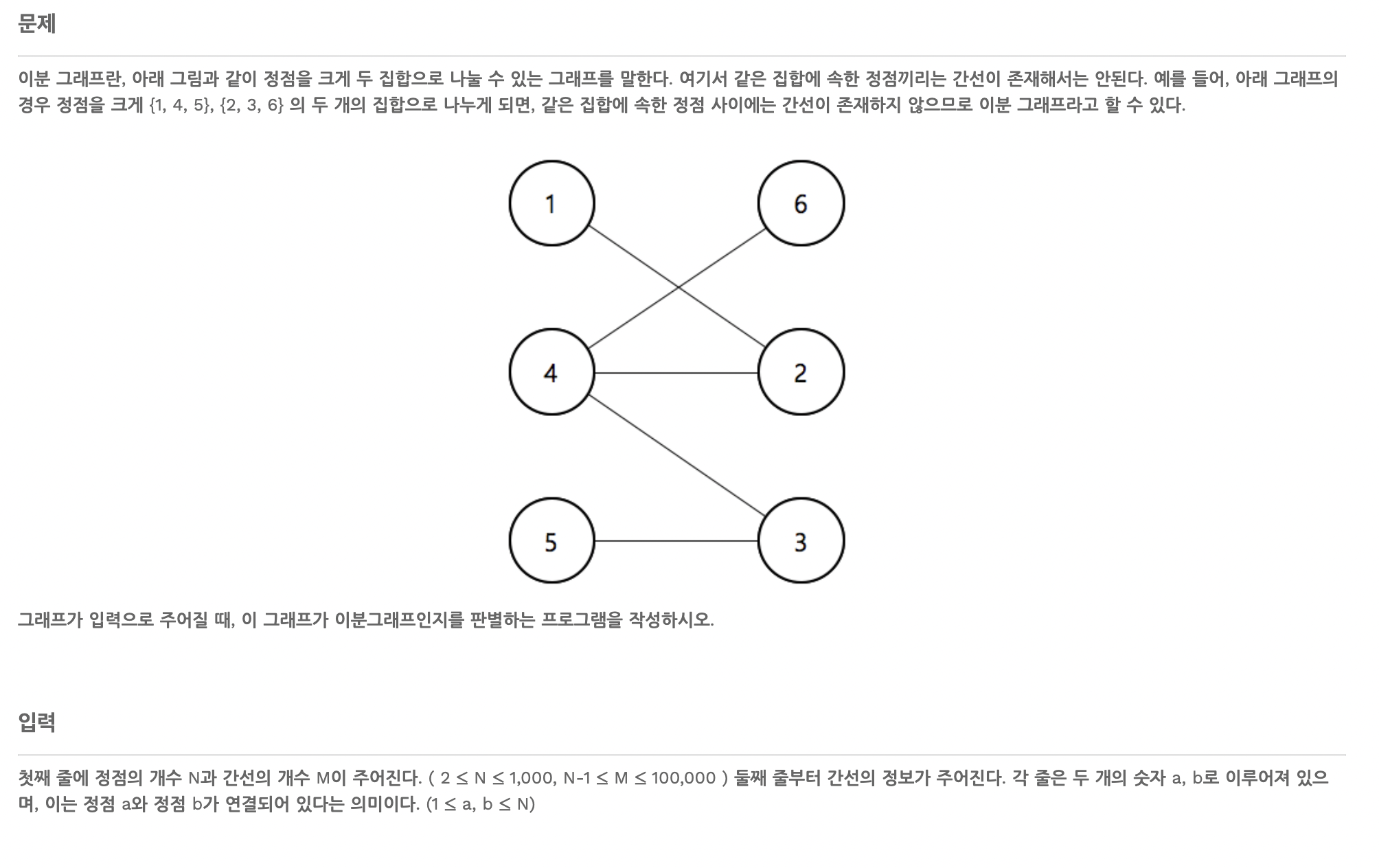
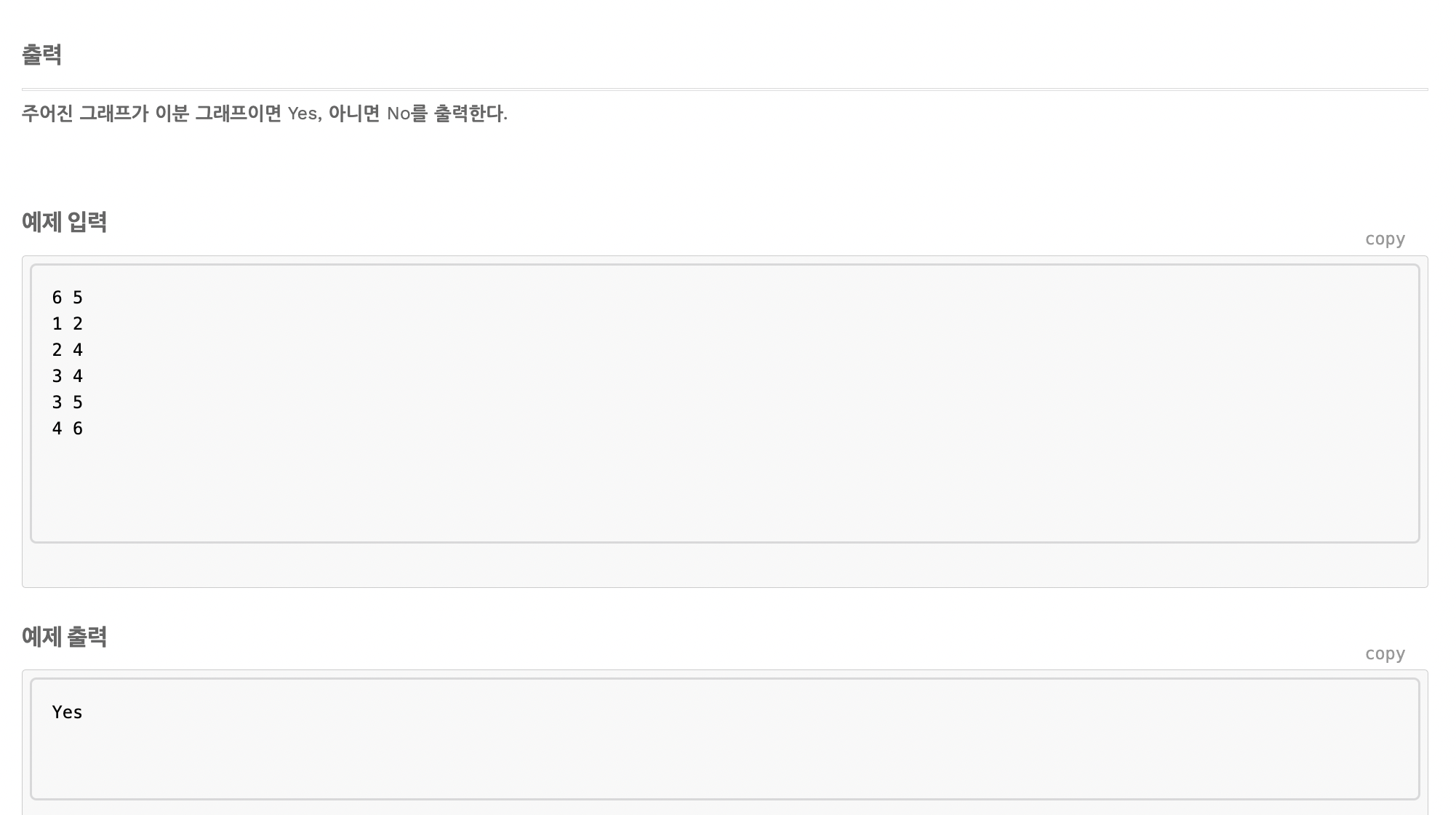
이분 그래프란 인접한 그래프와 간선이 연결되어 있으면 안 된다는 것이다.
import java.util.Scanner;
public class Main{
static int node;
static boolean map[][];
static int visited[];
static boolean result = true;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
node = sc.nextInt();
int edge = sc.nextInt();
map = new boolean[node +1][node +1];
visited = new int[node +1];
for (int i = 0;i<edge;i++){
int a = sc.nextInt();
int b = sc.nextInt();
map[a][b] = true;
map[b][a] = true;
}
DFS(1,false);
if (result) System.out.println("YES");
else System.out.println("NO");
}
static void DFS(int x, boolean check){
//false : 1 true : 2
if (visited[x]>0)
return;
if (check){
visited[x] = 2;
}
else visited[x] = 1;
for (int i = 1; i<= node; i++) {
if (map[x][i]) {
if (visited[i] == visited[x]) {
result = false;
return;
}
else if (visited[i]==0) DFS(i,!check);
}
}
}
}이 문제는 인접 배열을 사용하였다.
본인과 인접한 노드에 다른 값을 넣는다. 만약 본인과 인접한 노드의 값이 같다면 이분 그래프가 아니라는 것을 의미한다.
visited [x] 값이 0보다 크다는 것은 이미 방문을 했다는 것이므로 넘어간다.
false는 1로 나타내고 true는 2의 값을 준다.
본인은 false를 인접한 가장 가까운 노드는 true를 준다.
이 과정을 반복하다가 만약 어떠한 인접한 노드들의 값이 (2,2)이거나 (1,1)이 되는 순간 이분 그래프가 아니게 된다.
단지 번호 붙이기

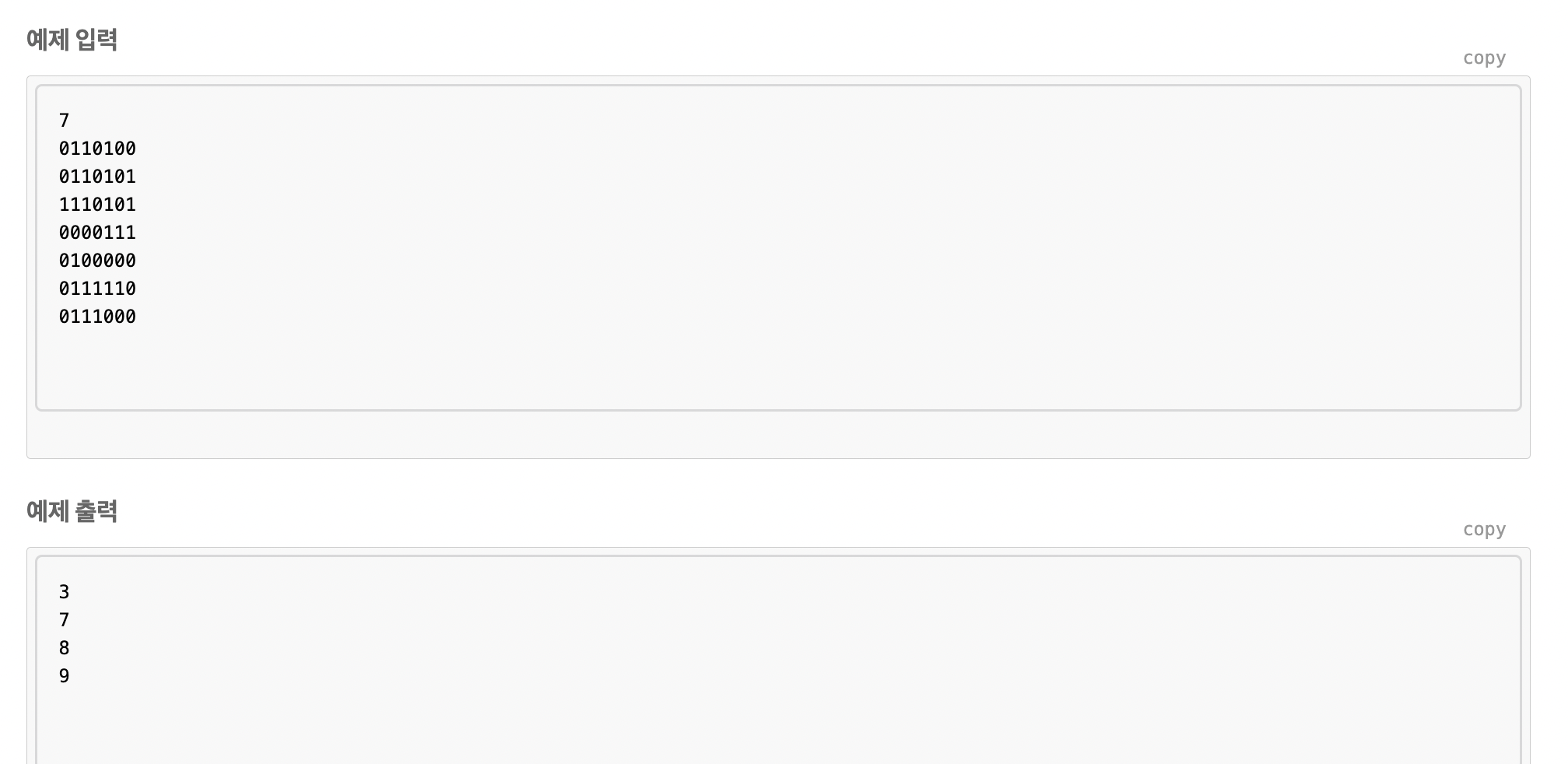
이 문제도 방문 여부가 중요하고, 양옆 위, 아래가 1의 값으로 연결되어 있다면 계속해서 DFS탐색을 한다.
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;
public class Main {
static int n;
static int count;
static int[] dx = {-1, 0, 1, 0};
static int[] dy = {0, -1, 0, 1};
static int[][] map;
static boolean[][] visited;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
StringBuilder sb = new StringBuilder();
List<Integer> list = new ArrayList<>();
n = sc.nextInt();
map = new int[n][n];
visited = new boolean[n][n];
for (int i = 0; i < n; i++) {
String str = sc.next();
for (int j = 0; j < n; j++) {
map[i][j] = (str.charAt(j)-'0');
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (map[i][j] == 1 && !visited[i][j]) {
count = 1;
list.add(DFS(i, j));
}
}
}
Collections.sort(list);
sb.append(list.size()).append("\n");
for (Integer i : list) {
sb.append(i).append("\n");
}
System.out.println(sb);
}
static int DFS(int x, int y) {
visited[x][y] = true;
for (int i = 0; i < 4; i++) {
int nextX = x + dx[i];
int nextY = y + dy[i];
if (nextX >= 0 && nextY >= 0 && nextX < n && nextY < n) {
if (!visited[nextX][nextY] && map[nextX][nextY] == 1) {
DFS(nextX, nextY);
count++;
}
}
}
return count;
}
}중요한 것은 dx, dy배열이다.
두 개의 배열을 보면 dx부터 [-1,0,1,0] , dy는 [0,-1,0,1]의 값을 가지고 있다.
두 개의 배열을 동시에 사용할 것인데, index가 0일 때 왼쪽으로, 1이면 아래로 2이면 오른쪽으로 3이면 위로 간다는 것을 의미한다.
2중 배열을 사용하여 전부 확인하는데, 이미 방문을 했거나, 1이 아니면 DFS탐색을 하지 않는다.
DFS메서드를 보면 아까 말했듯이 본인의 방문을 true로 만들고 양옆, 위아래를 DFS 탐색한다.
계속해서 탐색하다가 1이 끝나는 시점이 되어서야 리턴하게 된다.
배운 점
저번에 그래프에 대해 공부했었는데, 바로 그래프를 활용해서 재미있었다. 또한 이해도 쉽게 되었다.
하지만 문제를 푸는데 생각보다 쉽지 않았다. 아직 부족한 부분이 많은 것 같다.
DFS를 언제 사용해야 하는지, 어디에 사용해야 하는지 익숙해져야 할 것 같다.
'PS > 알고리즘' 카테고리의 다른 글
| 다익스트라 (0) | 2022.12.18 |
|---|---|
| 너비 우선 탐색(BFS) (1) | 2022.11.14 |
| 자료구조(Graph) (2) | 2022.11.02 |
| 자료구조(Tree) (0) | 2022.10.31 |
| 자료구조(Stack&Queue) (0) | 2022.10.26 |
그래프 순회
- 그래프라는 자료구조에 어떠한 값이 저장되어 있는가?
깊이 우선 탐색(Depth First Search)
스택을 이용하여 그래프를 순회하는 방법
스택 = 선행 관계
- 나를 먼저 방문하고 그다음으로 인접한 노드를 차례로 방문(단, 방문했던 노드는 방문하지 않는다.)
깊이 우선 탐색의 예시

위 그래프는 1 - 2 - 3 - 4 - 5 - 6 순으로 방문하게 된다.
중요한 점은 더 이상 갈 곳이 없다면, 왔던 곳으로 돌아간다.(재귀)
좀 더 복잡해 보이는 그래프를 보자.

위에 보이는 순서대로 방문하게 되고, 화살표의 모양대로 다시 돌아오게 된다.
가장 깊은 4까지 간 뒤 더 이상 갈 곳이 없기 때문에 돌아오면서 방문하지 못한 곳을 방문하게 된다.
DFS 구현
DFS를 구현하고, 코드를 보며 자세하게 알아보자.
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
static List<Integer>[] graph;
static boolean[] visited;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int Node = sc.nextInt();
int Edge = sc.nextInt();
visited = new boolean[Node+1];
graph = new ArrayList[Node+1];
for (int i = 1; i <=Node; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < Edge; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
}
DFS(1);
}
//x부터 DFS시작
static void DFS(int x) {
visited[x] = true;
System.out.printf("%d ",x);
for (int i=0;i<graph[x].size();i++){
int y = graph[x].get(i);
if (visited[y]==false){
DFS(y);
}
}
}
}인접 배열과 인접 리스트 중 한 가지를 선택하여 구현할 수 있는데, 이번 구현은 인접 리스트를 사용하였다.
우리가 볼 부분은 DFS 메서드이다.
이미 방문한 곳은 재 방문하지 않기 위해 visted [x]를 true로 선언한다.
그리고 그때 값을 출력해준다.
for문에서 graph는 인접 리스트를 사용하였으므로, 인접한 노드들이 담겨있다.
따라서 y는 인접한 노드 중 숫자가 작은 값부터 DFS로 들어가게 된다.
DFS의 정확성 / 시간 복잡도
DFS가 정말 순회를 하는가?
모든 정점을 방문한다. 하나의 정점을 두 번 이상 방문하지 않는다.
자신을 방문하고, 모든 이웃에게 물어봄 -> |V| = 2*|E|
각 정점은 1번씩, 각 간선은 2번씩 방문한다.
따라서 O(V+E)의 시간 복잡도를 갖게 된다.
DFS 활용 문제를 풀어보자
웜 바이러스


DFS를 이용하여 전부 탐색하고, 그 횟수를 찾으면 된다.
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main{
static List<Integer>[] graph;
static boolean[] visited;
static int count=-1;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int node = sc.nextInt();
int edge = sc.nextInt();
graph = new List[node+1];
visited = new boolean[node+1];
for (int i=1; i<=node;i++){
graph[i] = new ArrayList<>();
}
for (int i = 0;i<edge;i++){
int a = sc.nextInt();
int b = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
}
DFS(1);
System.out.println(count);
}
static void DFS(int x){
visited[x] = true;
count++;
for (int i=0;i<graph[x].size();i++){
int y = graph[x].get(i);
if (visited[y]==false){
DFS(y);
}
}
}
}우리가 구현한 DFS와 거의 흡사하다.
우리가 중요한 것은 총 방문한 노드의 수이므로 방문을 할 때마다 count를 증가시킨다.
여기서 중요한 점은 본인을 방문한 경우는 삐야 하므로 count = -1에서 시작한다.
이분 그래프 판별


이분 그래프란 인접한 그래프와 간선이 연결되어 있으면 안 된다는 것이다.
import java.util.Scanner;
public class Main{
static int node;
static boolean map[][];
static int visited[];
static boolean result = true;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
node = sc.nextInt();
int edge = sc.nextInt();
map = new boolean[node +1][node +1];
visited = new int[node +1];
for (int i = 0;i<edge;i++){
int a = sc.nextInt();
int b = sc.nextInt();
map[a][b] = true;
map[b][a] = true;
}
DFS(1,false);
if (result) System.out.println("YES");
else System.out.println("NO");
}
static void DFS(int x, boolean check){
//false : 1 true : 2
if (visited[x]>0)
return;
if (check){
visited[x] = 2;
}
else visited[x] = 1;
for (int i = 1; i<= node; i++) {
if (map[x][i]) {
if (visited[i] == visited[x]) {
result = false;
return;
}
else if (visited[i]==0) DFS(i,!check);
}
}
}
}이 문제는 인접 배열을 사용하였다.
본인과 인접한 노드에 다른 값을 넣는다. 만약 본인과 인접한 노드의 값이 같다면 이분 그래프가 아니라는 것을 의미한다.
visited [x] 값이 0보다 크다는 것은 이미 방문을 했다는 것이므로 넘어간다.
false는 1로 나타내고 true는 2의 값을 준다.
본인은 false를 인접한 가장 가까운 노드는 true를 준다.
이 과정을 반복하다가 만약 어떠한 인접한 노드들의 값이 (2,2)이거나 (1,1)이 되는 순간 이분 그래프가 아니게 된다.
단지 번호 붙이기


이 문제도 방문 여부가 중요하고, 양옆 위, 아래가 1의 값으로 연결되어 있다면 계속해서 DFS탐색을 한다.
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;
public class Main {
static int n;
static int count;
static int[] dx = {-1, 0, 1, 0};
static int[] dy = {0, -1, 0, 1};
static int[][] map;
static boolean[][] visited;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
StringBuilder sb = new StringBuilder();
List<Integer> list = new ArrayList<>();
n = sc.nextInt();
map = new int[n][n];
visited = new boolean[n][n];
for (int i = 0; i < n; i++) {
String str = sc.next();
for (int j = 0; j < n; j++) {
map[i][j] = (str.charAt(j)-'0');
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (map[i][j] == 1 && !visited[i][j]) {
count = 1;
list.add(DFS(i, j));
}
}
}
Collections.sort(list);
sb.append(list.size()).append("\n");
for (Integer i : list) {
sb.append(i).append("\n");
}
System.out.println(sb);
}
static int DFS(int x, int y) {
visited[x][y] = true;
for (int i = 0; i < 4; i++) {
int nextX = x + dx[i];
int nextY = y + dy[i];
if (nextX >= 0 && nextY >= 0 && nextX < n && nextY < n) {
if (!visited[nextX][nextY] && map[nextX][nextY] == 1) {
DFS(nextX, nextY);
count++;
}
}
}
return count;
}
}중요한 것은 dx, dy배열이다.
두 개의 배열을 보면 dx부터 [-1,0,1,0] , dy는 [0,-1,0,1]의 값을 가지고 있다.
두 개의 배열을 동시에 사용할 것인데, index가 0일 때 왼쪽으로, 1이면 아래로 2이면 오른쪽으로 3이면 위로 간다는 것을 의미한다.
2중 배열을 사용하여 전부 확인하는데, 이미 방문을 했거나, 1이 아니면 DFS탐색을 하지 않는다.
DFS메서드를 보면 아까 말했듯이 본인의 방문을 true로 만들고 양옆, 위아래를 DFS 탐색한다.
계속해서 탐색하다가 1이 끝나는 시점이 되어서야 리턴하게 된다.
배운 점
저번에 그래프에 대해 공부했었는데, 바로 그래프를 활용해서 재미있었다. 또한 이해도 쉽게 되었다.
하지만 문제를 푸는데 생각보다 쉽지 않았다. 아직 부족한 부분이 많은 것 같다.
DFS를 언제 사용해야 하는지, 어디에 사용해야 하는지 익숙해져야 할 것 같다.
'PS > 알고리즘' 카테고리의 다른 글
| 다익스트라 (0) | 2022.12.18 |
|---|---|
| 너비 우선 탐색(BFS) (1) | 2022.11.14 |
| 자료구조(Graph) (2) | 2022.11.02 |
| 자료구조(Tree) (0) | 2022.10.31 |
| 자료구조(Stack&Queue) (0) | 2022.10.26 |
