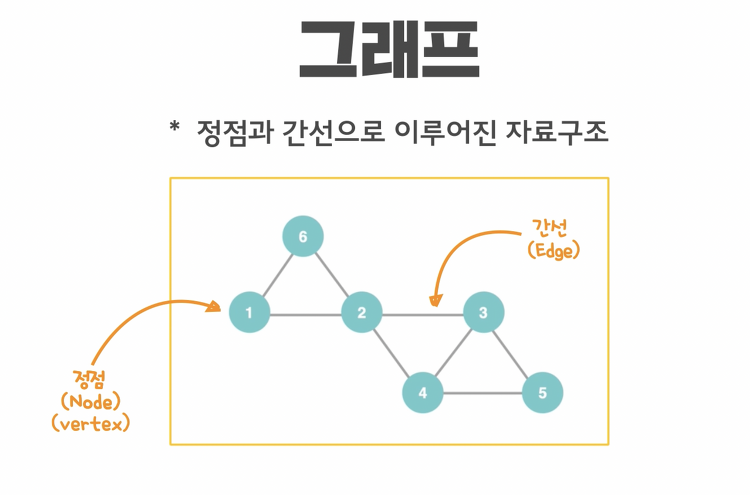
그래프란 다음과 같은 모습을 가지고 있다.
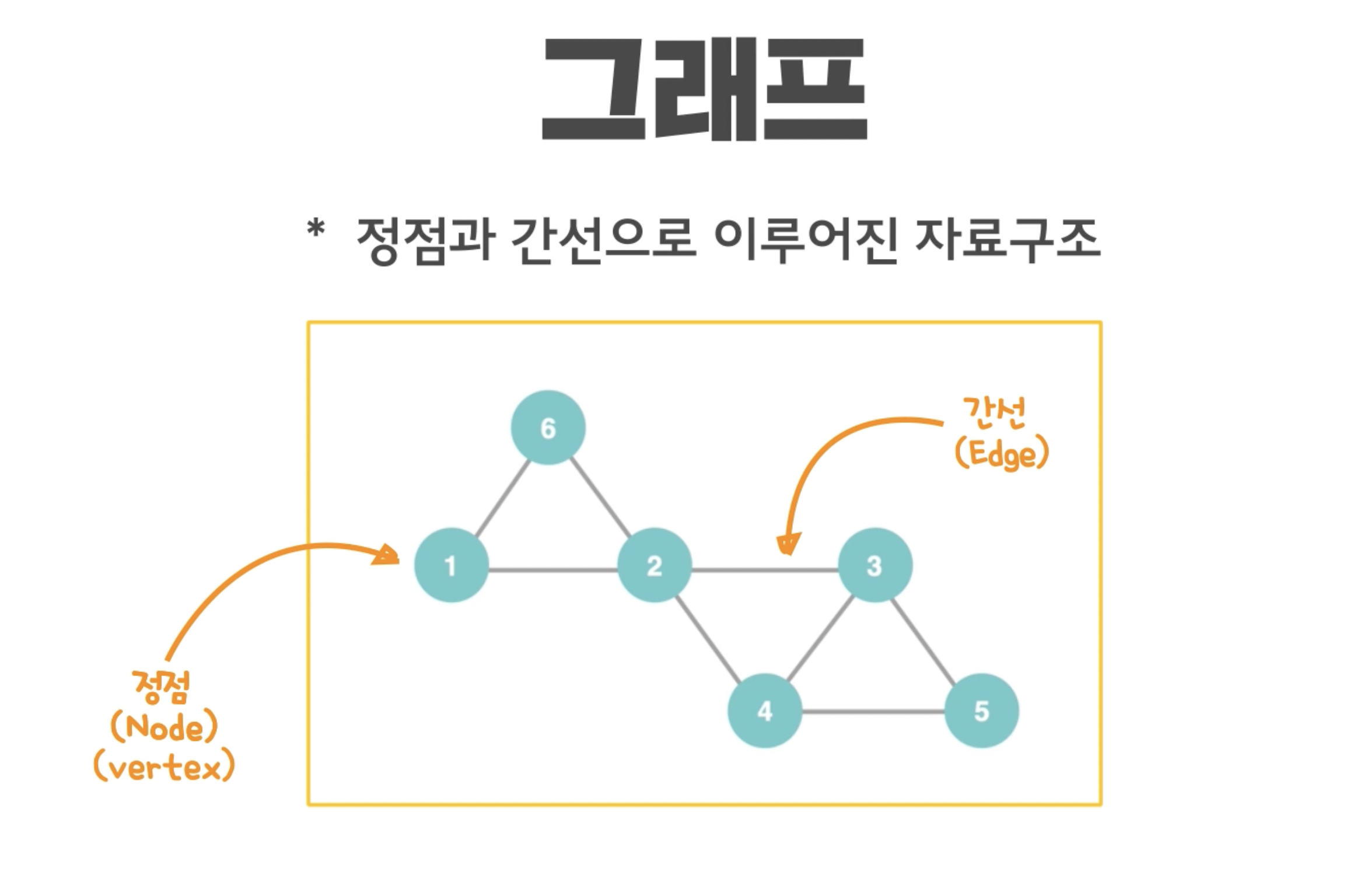
즉 그래프는 각각의 정점이 간선으로 연결되어있는 모습이다.
그래프는 왜 중요한가?
현실 세계의 많은 것들을 그래프로 나타낼 수 있다.
- 즉 그래프와 관련된 문제가 매우 많다.
그래프와 관련된 수학적 정리가 매우 많다.
- 그래프 이론이라는 분야가 따로 있다.
그래프에 관한 중요한 수학적 지식
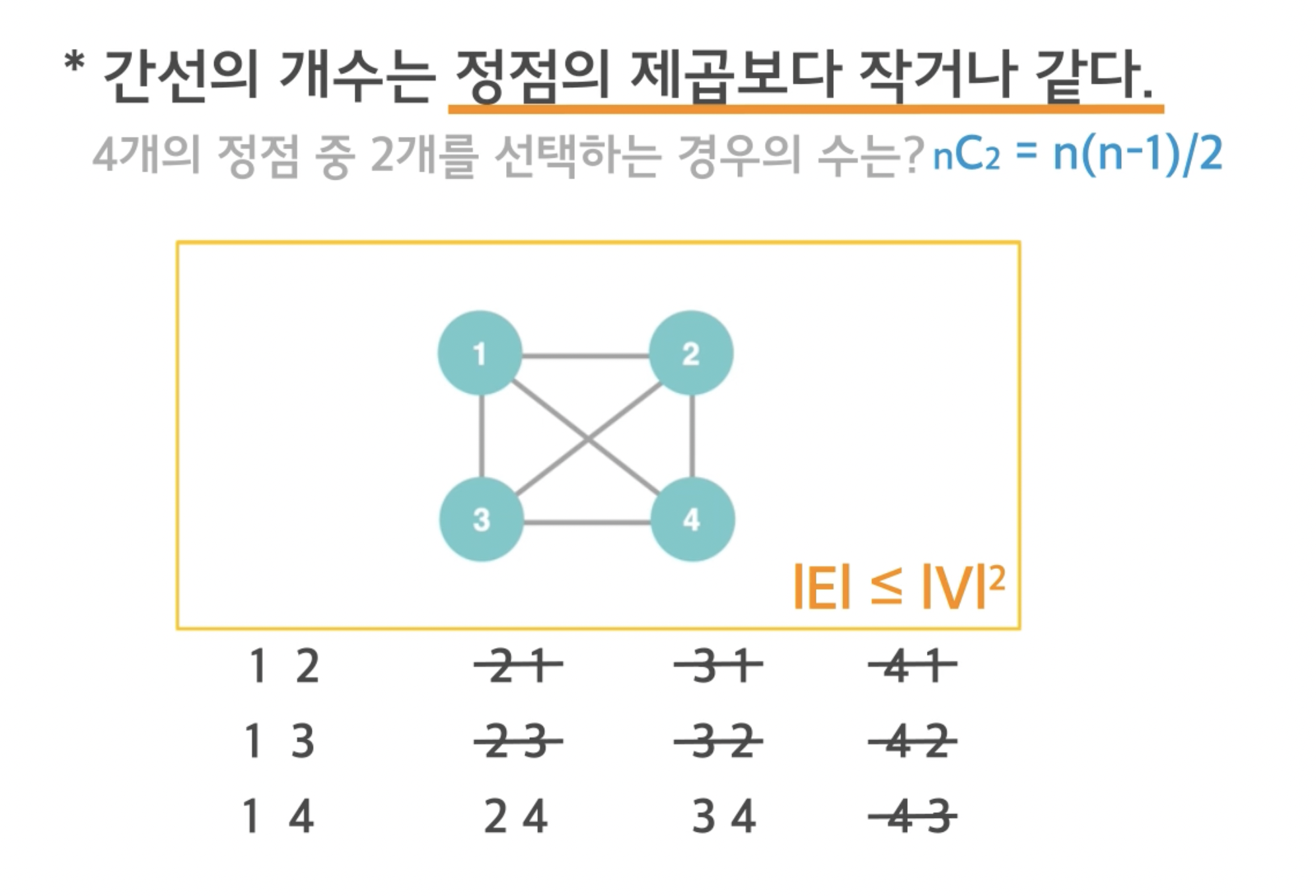
간선의 개수는 정점의 제곱보다 작거나 같다. -> 항상 참
각 정점의 차수의 합은 간선의 개수의 2배와 같다. -> 항상 참
- 차수는 각 정점에 연결되어 있는 간선의 수
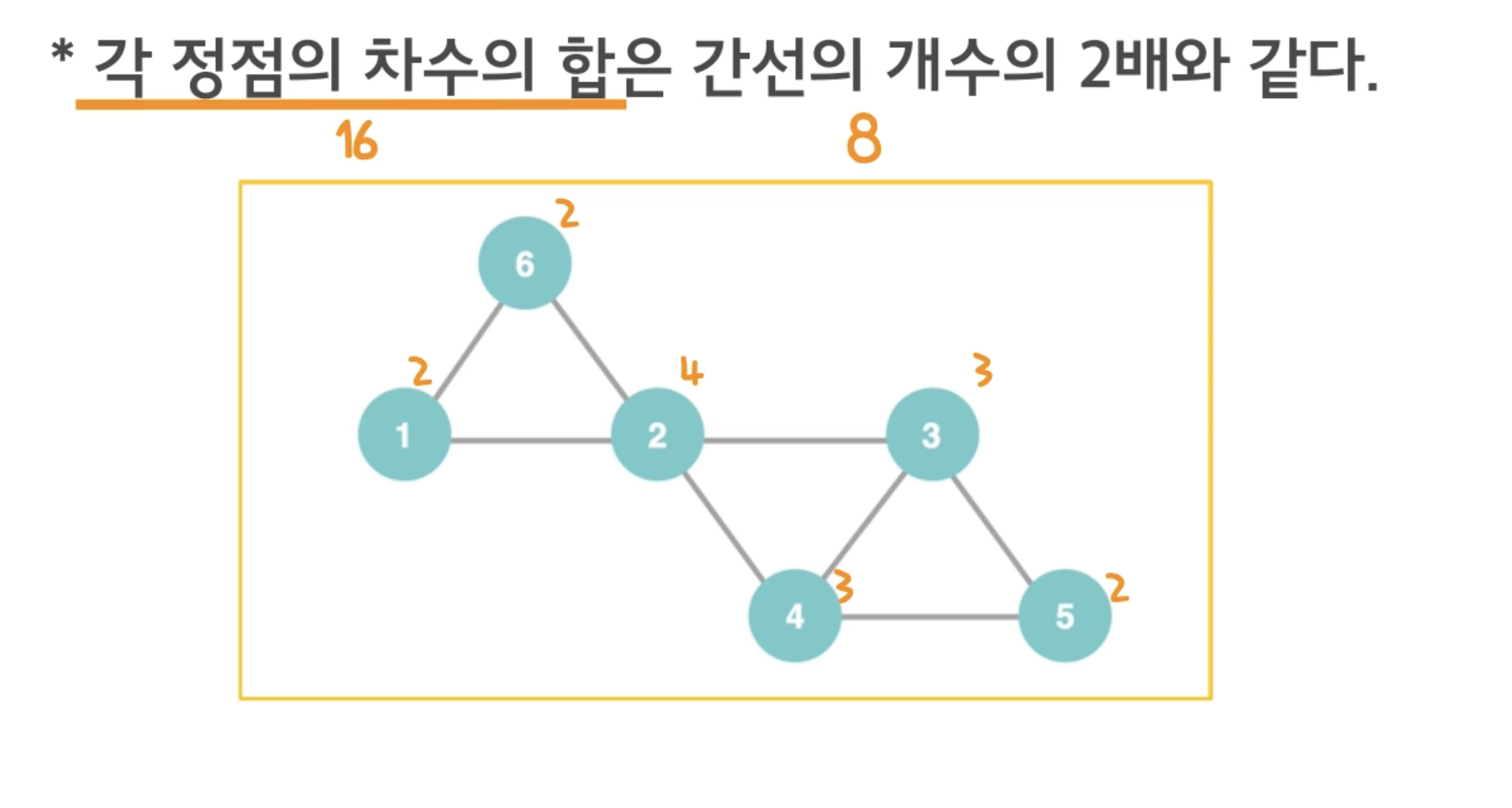
차수의 합을 구할 때, 각 간선을 두 번씩 세기 때문이다.
그래프의 구현 : 인접 행렬
정점의 연결 관계를 2차원 배열에 0,1로 표현한다.
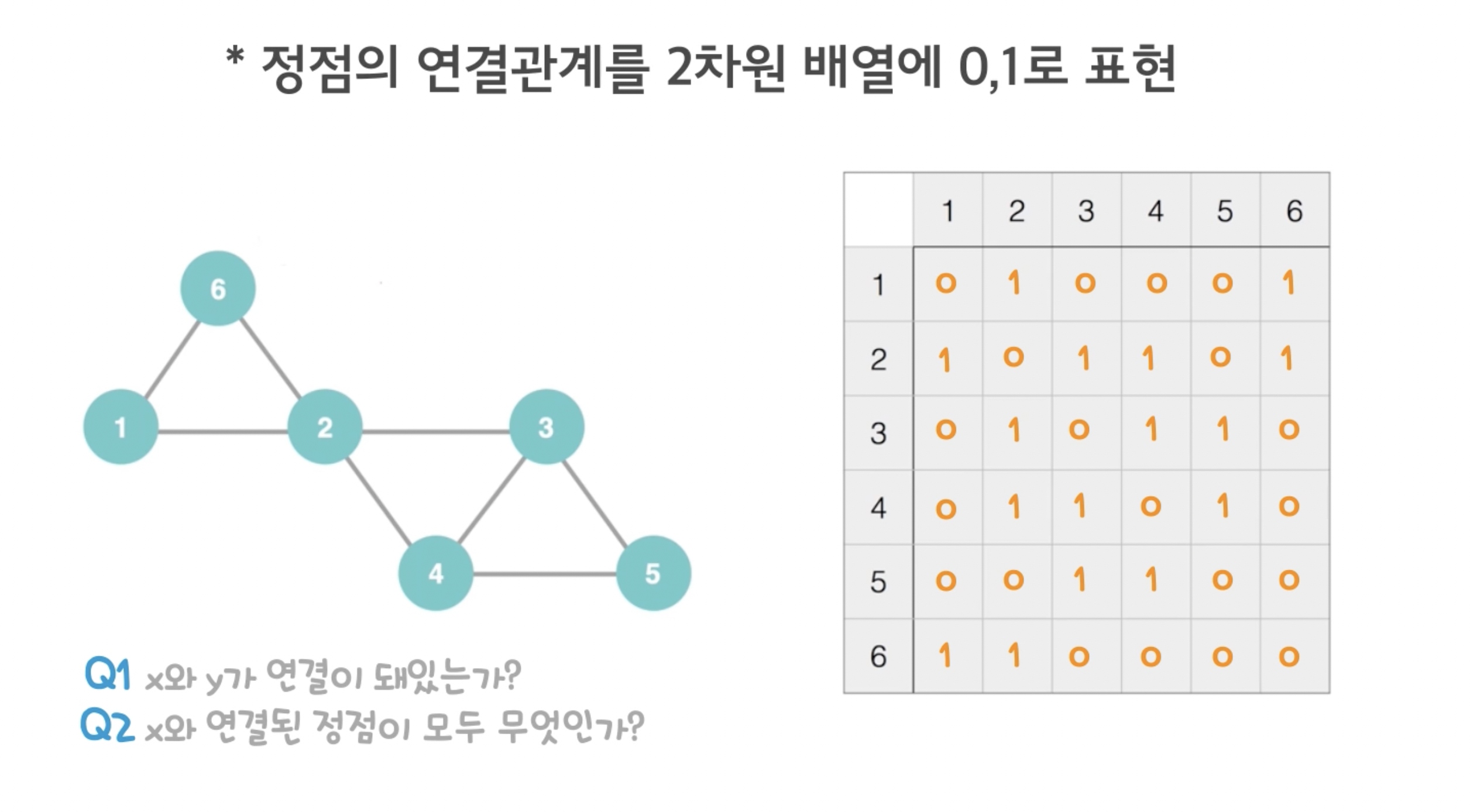
장점: 연결 여부를 O(1)에 알 수 있다.
단점: 인접한 정점을 찾는데 O(n)이 걸린다. - 실제 인접한 정점 수 와 관계없이
단점: 무조건 n^2개의 칸을 써야 한다. - 실제 간선의 개수와 관계없이
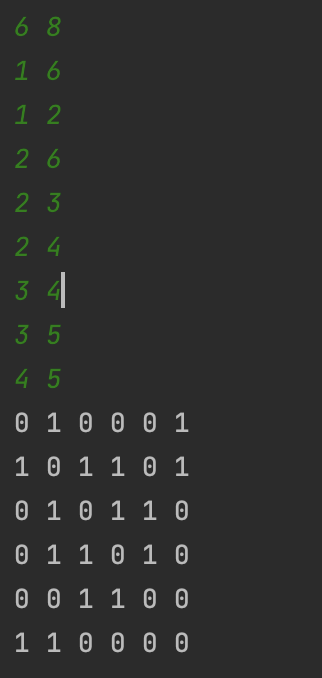
그래프 구현하기 - 인접 행렬
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // 정점의 갯수
int m = sc.nextInt(); // 간선의 갯수
int[][] graph = new int[n+1][n+1];
for (int i=0;i<m;i++){
int a = sc.nextInt();
int b = sc.nextInt();
graph[a][b] = 1;
graph[b][a] = 1;
}
for (int i=1;i<=n;i++){
for (int j =1;j<=n;j++){
System.out.print(graph[i][j]+" ");
}
System.out.println();
}
}
}위의 그림과 같이 연결시키면 우리가 예상한 그래프가 나오게 된다.
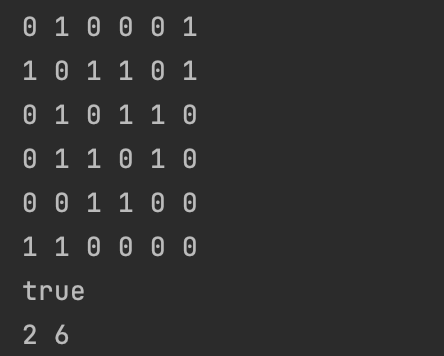
그래프를 이용해서 각 정점이 연결되어있는지, 한 정점에 연결되어있는 정점은 무엇인지 알 수 있다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // 정점의 갯수
int m = sc.nextInt(); // 간선의 갯수
int[][] graph = new int[n+1][n+1];
for (int i=0;i<m;i++){
int a = sc.nextInt();
int b = sc.nextInt();
graph[a][b] = 1;
graph[b][a] = 1;
}
for (int i=1;i<=n;i++){
for (int j =1;j<=n;j++){
System.out.print(graph[i][j]+" ");
}
System.out.println();
}
System.out.println(isConnected(graph,1,2)); //Q. 정점X,Y가 연결되어있는가?
getAdj(graph,n,1);//Q. graph에서 x와 연결되어 있는 모든 정점이 무엇인가?
}
//Q. 정점X,Y가 연결되어있는지 확인
static boolean isConnected(int[][] graph,int x,int y){
return graph[x][y]==1?true:false;
}
//Q. graph에서 x와 연결되어 있는 모든 정점을 출력
static void getAdj(int[][] graph,int n, int x){
for (int i=1;i<=n;i++){
if (graph[x][i]==1) System.out.print(i+" ");
}
}
}이미 그래프를 만들었기 때문에 두 가지 질문을 쉽게 답할 수 있다.
그래프의 구현 : 인접 리스트
각각의 정점에 연결된 정점의 번호만을 저장한다.
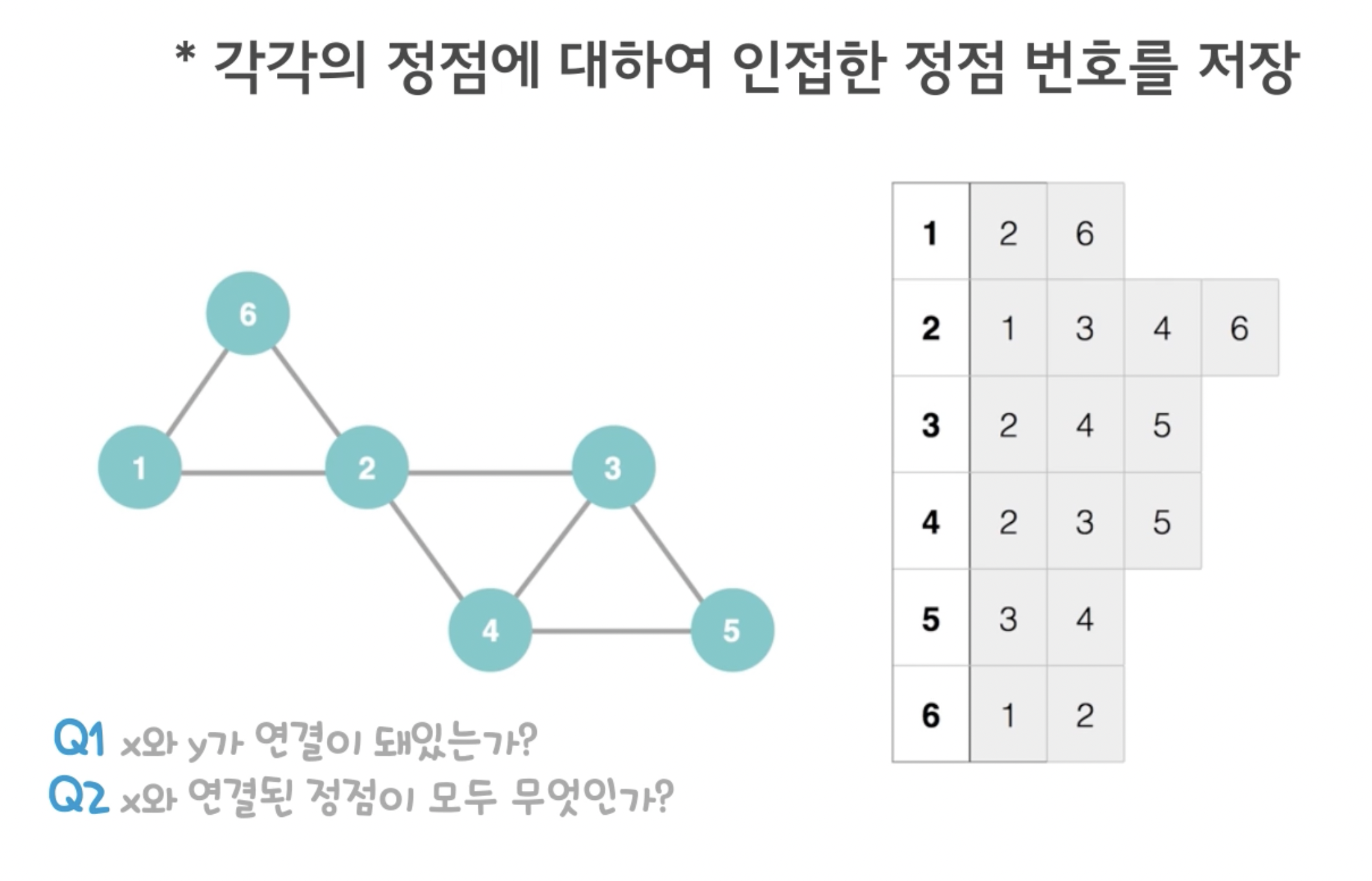
장점: 인접한 정점을 모두 찾는데 필요한 만큼만 본다.
장점: 필요한 만큼만 공간을 활용한다.
단점: 인접 여부를 보려면 인접한 정점을 모두 봐야 한다. - O(deg(v)) (ex) 2의 경우 4번을 확인해야 함
여기서 의문점이 들 수 있다.
인접 리스트를 보면 각 배열의 크기가 다르다.
이를 해결하기 위해 우리는 Vector를 사용해야 한다.
Vector는 크기를 지정하지 않고 값을 추가하거나, 삭제할 수 있는 장점이 있다.
즉 각각의 배열 크기를 우리가 원하는 대로 설정할 수 있다.
사실 Vector보다 List를 사용하는 것을 권장한다.
이번 글에서는 Vector를 사용할 것이다.
그래프 구현하기 - 인접 리스트
import java.util.Scanner;
import java.util.Vector;
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
Vector<Integer>[] graph = new Vector[n+1];
for (int i=0;i<n+1;i++){
graph[i] = new Vector<>();
}
for (int i =0;i<m;i++){
int a = sc.nextInt();
int b = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
}
for (int i=1;i<=n;i++){
for (int j =0;j<graph[i].size();j++){
System.out.print(graph[i].get(j)+" ");
}
System.out.println();
}
}
}여기서 중요한 점은 Vector를 배열로 나누어 사용할 경우 각각 다시 초기화해주어야 한다.
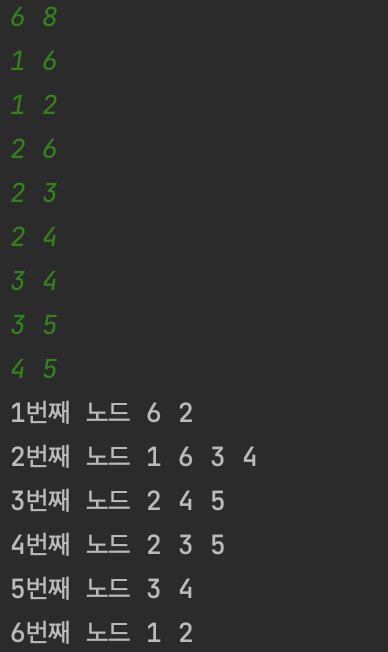
각 노드의 값들이 정렬되지 않은 이유는 넣는 순서 때문이다.
이 그래프를 이용하여 두 가지 질문에 답해보자.
import java.util.Scanner;
import java.util.Vector;
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
Vector<Integer>[] graph = new Vector[n+1];
for (int i=0;i<n+1;i++){
graph[i] = new Vector<>();
}
for (int i =0;i<m;i++){
int a = sc.nextInt();
int b = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
}
for (int i=1;i<=n;i++){
System.out.printf("%d번째배열 ",i);
for (int j =0;j<graph[i].size();j++){
System.out.print(graph[i].get(j)+" ");
}
System.out.println();
}
System.out.println(isConnected(graph,1,2));
getAdj(graph,6);
}
static boolean isConnected(Vector[] graph,int x,int y){
return graph[x].contains(y)?true:false;
}
static void getAdj(Vector[] graph,int x){
for (int i=0;i<=graph[x].size()-1;i++){
System.out.print(graph[x].get(i)+" ");
}
}
}그래프를 이용하여 정점에 근접한 정점을 쉽게 구할 수 있고, 두 정점이 인접했는지 알 수도 있다.
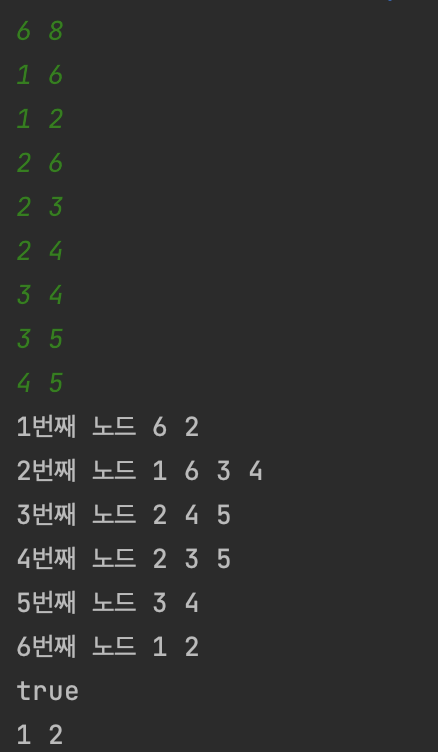
배운 점
그래프를 구현해보면서 그래프의 장점에 대해 알게 되었다.
인접 행렬과 인접 리스트의 각 장단점을 알게 되었고, 그로 인해 각 상황에 맞게 좋은 것을 사용해야 한다는 것을 알았다.
인접 리스트를 구현하면서 Vector배열을 만들어봤다. 이때 각각을 초기화하지 않아 오류가 떴었다.
이를 통해 초기화를 간과하고 있었다는 실수를 알았고, 기초를 더욱 탄탄하게 잡아야 한다고 느꼈다.
'PS > 알고리즘' 카테고리의 다른 글
| 너비 우선 탐색(BFS) (1) | 2022.11.14 |
|---|---|
| 깊이 우선 탐색(DFS) (2) | 2022.11.06 |
| 자료구조(Tree) (0) | 2022.10.31 |
| 자료구조(Stack&Queue) (0) | 2022.10.26 |
| 이진탐색 (0) | 2022.10.21 |
그래프란 다음과 같은 모습을 가지고 있다.

즉 그래프는 각각의 정점이 간선으로 연결되어있는 모습이다.
그래프는 왜 중요한가?
현실 세계의 많은 것들을 그래프로 나타낼 수 있다.
- 즉 그래프와 관련된 문제가 매우 많다.
그래프와 관련된 수학적 정리가 매우 많다.
- 그래프 이론이라는 분야가 따로 있다.
그래프에 관한 중요한 수학적 지식
간선의 개수는 정점의 제곱보다 작거나 같다. -> 항상 참

각 정점의 차수의 합은 간선의 개수의 2배와 같다. -> 항상 참
- 차수는 각 정점에 연결되어 있는 간선의 수

차수의 합을 구할 때, 각 간선을 두 번씩 세기 때문이다.
그래프의 구현 : 인접 행렬
정점의 연결 관계를 2차원 배열에 0,1로 표현한다.

장점: 연결 여부를 O(1)에 알 수 있다.
단점: 인접한 정점을 찾는데 O(n)이 걸린다. - 실제 인접한 정점 수 와 관계없이
단점: 무조건 n^2개의 칸을 써야 한다. - 실제 간선의 개수와 관계없이
그래프 구현하기 - 인접 행렬
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // 정점의 갯수
int m = sc.nextInt(); // 간선의 갯수
int[][] graph = new int[n+1][n+1];
for (int i=0;i<m;i++){
int a = sc.nextInt();
int b = sc.nextInt();
graph[a][b] = 1;
graph[b][a] = 1;
}
for (int i=1;i<=n;i++){
for (int j =1;j<=n;j++){
System.out.print(graph[i][j]+" ");
}
System.out.println();
}
}
}위의 그림과 같이 연결시키면 우리가 예상한 그래프가 나오게 된다.

그래프를 이용해서 각 정점이 연결되어있는지, 한 정점에 연결되어있는 정점은 무엇인지 알 수 있다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // 정점의 갯수
int m = sc.nextInt(); // 간선의 갯수
int[][] graph = new int[n+1][n+1];
for (int i=0;i<m;i++){
int a = sc.nextInt();
int b = sc.nextInt();
graph[a][b] = 1;
graph[b][a] = 1;
}
for (int i=1;i<=n;i++){
for (int j =1;j<=n;j++){
System.out.print(graph[i][j]+" ");
}
System.out.println();
}
System.out.println(isConnected(graph,1,2)); //Q. 정점X,Y가 연결되어있는가?
getAdj(graph,n,1);//Q. graph에서 x와 연결되어 있는 모든 정점이 무엇인가?
}
//Q. 정점X,Y가 연결되어있는지 확인
static boolean isConnected(int[][] graph,int x,int y){
return graph[x][y]==1?true:false;
}
//Q. graph에서 x와 연결되어 있는 모든 정점을 출력
static void getAdj(int[][] graph,int n, int x){
for (int i=1;i<=n;i++){
if (graph[x][i]==1) System.out.print(i+" ");
}
}
}이미 그래프를 만들었기 때문에 두 가지 질문을 쉽게 답할 수 있다.

그래프의 구현 : 인접 리스트
각각의 정점에 연결된 정점의 번호만을 저장한다.

장점: 인접한 정점을 모두 찾는데 필요한 만큼만 본다.
장점: 필요한 만큼만 공간을 활용한다.
단점: 인접 여부를 보려면 인접한 정점을 모두 봐야 한다. - O(deg(v)) (ex) 2의 경우 4번을 확인해야 함
여기서 의문점이 들 수 있다.
인접 리스트를 보면 각 배열의 크기가 다르다.
이를 해결하기 위해 우리는 Vector를 사용해야 한다.
Vector는 크기를 지정하지 않고 값을 추가하거나, 삭제할 수 있는 장점이 있다.
즉 각각의 배열 크기를 우리가 원하는 대로 설정할 수 있다.
사실 Vector보다 List를 사용하는 것을 권장한다.
이번 글에서는 Vector를 사용할 것이다.
그래프 구현하기 - 인접 리스트
import java.util.Scanner;
import java.util.Vector;
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
Vector<Integer>[] graph = new Vector[n+1];
for (int i=0;i<n+1;i++){
graph[i] = new Vector<>();
}
for (int i =0;i<m;i++){
int a = sc.nextInt();
int b = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
}
for (int i=1;i<=n;i++){
for (int j =0;j<graph[i].size();j++){
System.out.print(graph[i].get(j)+" ");
}
System.out.println();
}
}
}여기서 중요한 점은 Vector를 배열로 나누어 사용할 경우 각각 다시 초기화해주어야 한다.

각 노드의 값들이 정렬되지 않은 이유는 넣는 순서 때문이다.
이 그래프를 이용하여 두 가지 질문에 답해보자.
import java.util.Scanner;
import java.util.Vector;
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
Vector<Integer>[] graph = new Vector[n+1];
for (int i=0;i<n+1;i++){
graph[i] = new Vector<>();
}
for (int i =0;i<m;i++){
int a = sc.nextInt();
int b = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
}
for (int i=1;i<=n;i++){
System.out.printf("%d번째배열 ",i);
for (int j =0;j<graph[i].size();j++){
System.out.print(graph[i].get(j)+" ");
}
System.out.println();
}
System.out.println(isConnected(graph,1,2));
getAdj(graph,6);
}
static boolean isConnected(Vector[] graph,int x,int y){
return graph[x].contains(y)?true:false;
}
static void getAdj(Vector[] graph,int x){
for (int i=0;i<=graph[x].size()-1;i++){
System.out.print(graph[x].get(i)+" ");
}
}
}그래프를 이용하여 정점에 근접한 정점을 쉽게 구할 수 있고, 두 정점이 인접했는지 알 수도 있다.

배운 점
그래프를 구현해보면서 그래프의 장점에 대해 알게 되었다.
인접 행렬과 인접 리스트의 각 장단점을 알게 되었고, 그로 인해 각 상황에 맞게 좋은 것을 사용해야 한다는 것을 알았다.
인접 리스트를 구현하면서 Vector배열을 만들어봤다. 이때 각각을 초기화하지 않아 오류가 떴었다.
이를 통해 초기화를 간과하고 있었다는 실수를 알았고, 기초를 더욱 탄탄하게 잡아야 한다고 느꼈다.
'PS > 알고리즘' 카테고리의 다른 글
| 너비 우선 탐색(BFS) (1) | 2022.11.14 |
|---|---|
| 깊이 우선 탐색(DFS) (2) | 2022.11.06 |
| 자료구조(Tree) (0) | 2022.10.31 |
| 자료구조(Stack&Queue) (0) | 2022.10.26 |
| 이진탐색 (0) | 2022.10.21 |