그래프를 활용하여 최단 경로를 구할 수는 없을까?
최단경로 알고리즘은 크게 3가지가 존재한다.

이번 시간에는 다익스트라만 다루도록 하겠다.
다익스트라란?
음의 가중치가 없는 그래프의 한 정점에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘이다.
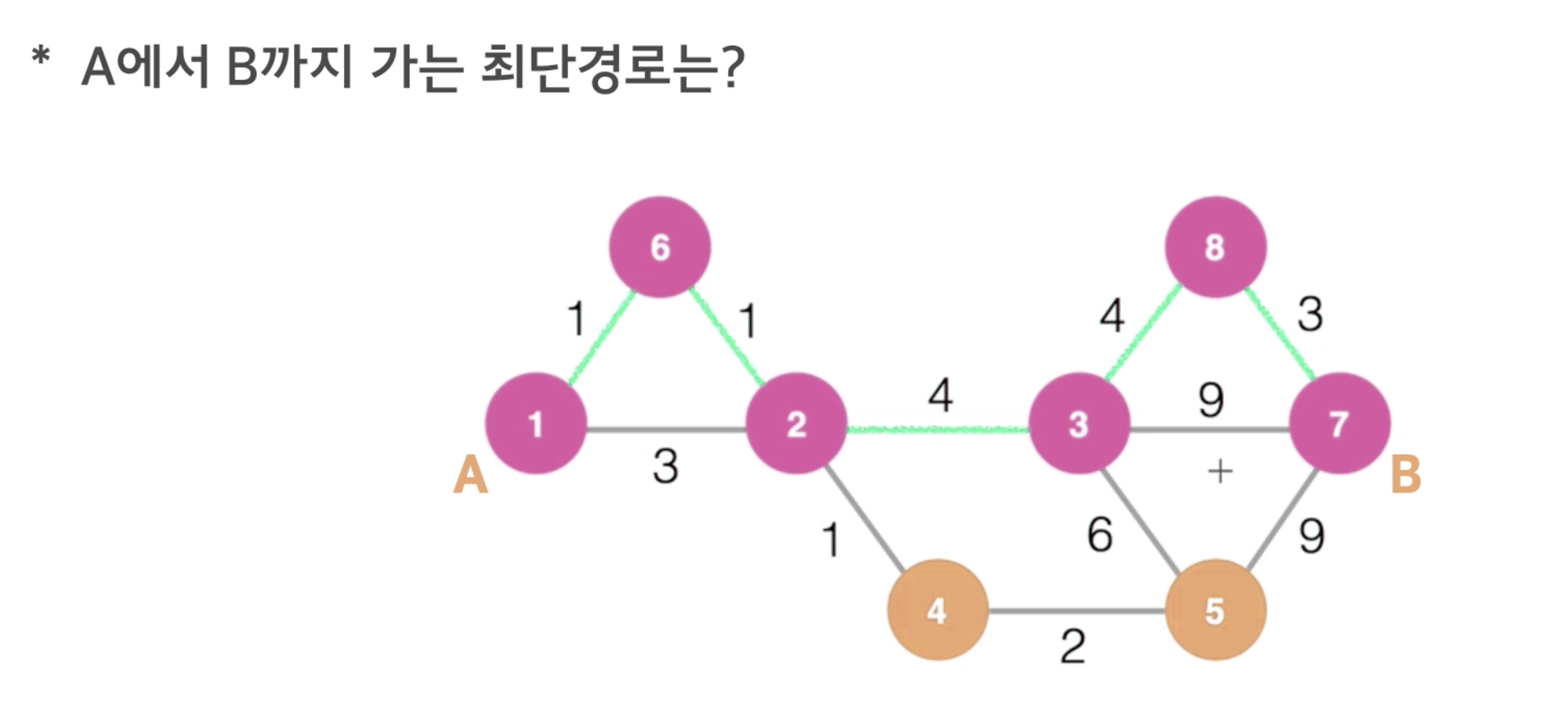
정점 사이에는 가중치가 존재한다.
최단경로의 특징
정점 x까지 최단거리로 가기 위해서는 그 직전까지도 최단거리로 가야 한다.
위의 그림을 보면 1 - 6 - 2 - 3 - 8 - 7 순으로 이동한다.
최단경로의 특징을 이용하면 1~8까지 이동할 때에도 최단 경로로 이동한다.
그래서 최단경로 트리를 어떻게 만들 것인가?
T(i) = i까지 도달하는 최단거리 -> 파란색 숫자
순서를 그림을 이용하여 천천히 설명하겠다.
보라 색원은 이미 탐색을 완료했다는 의미이다.
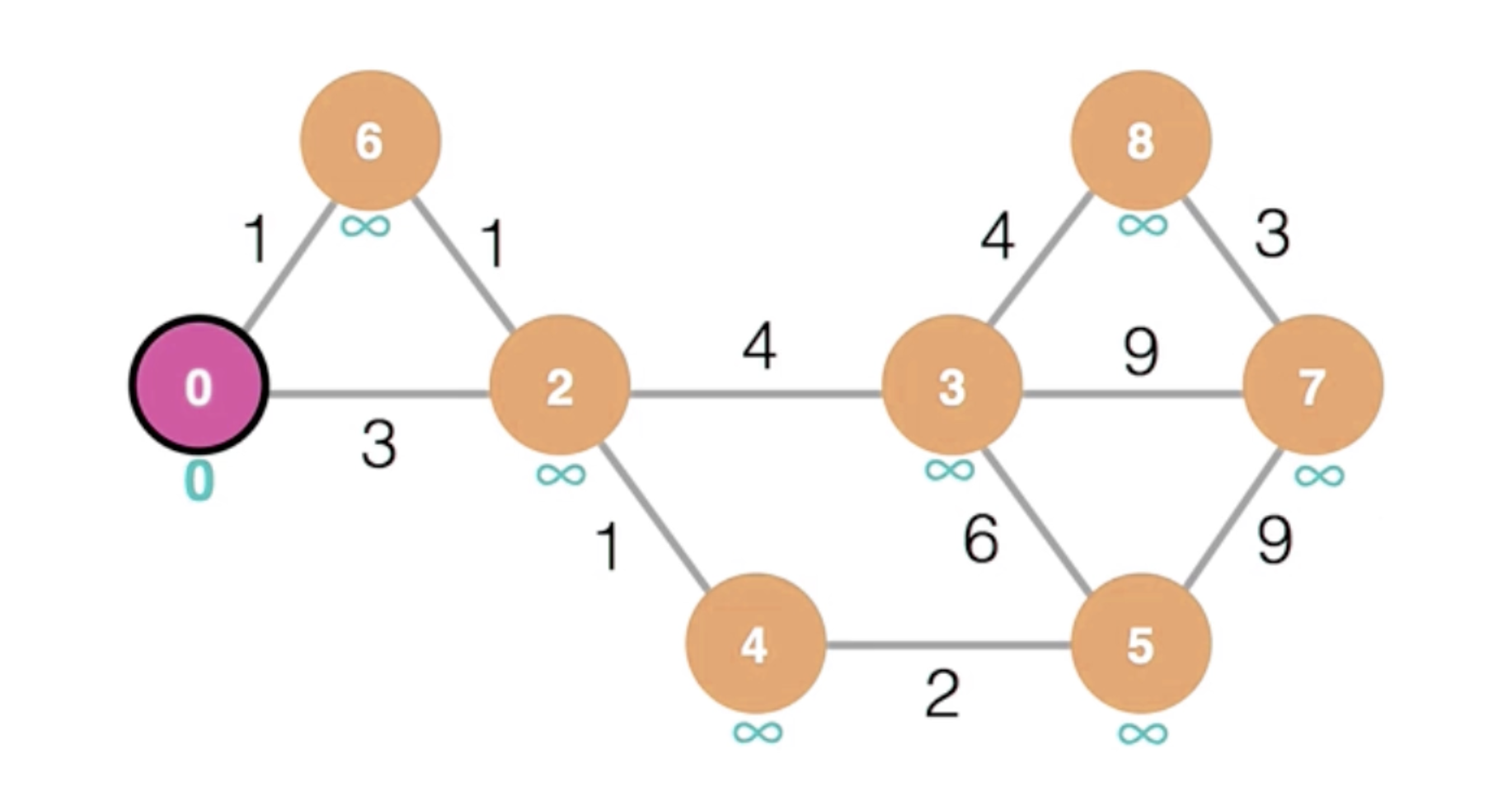
처음 시작점을 0으로 두고 나머지는 무한대로 설정한다.
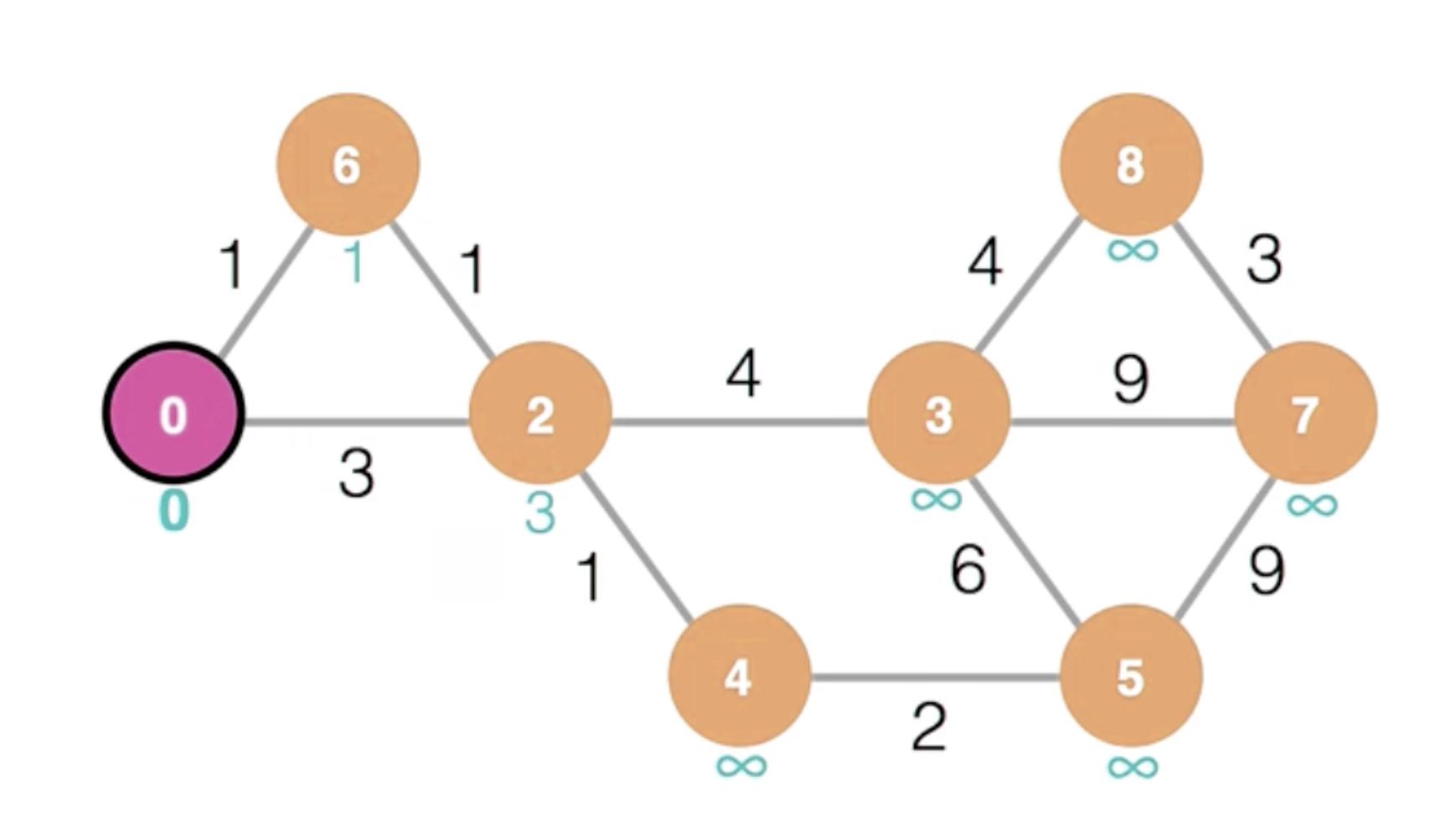
인접한 노드의 거리를 설정한다.
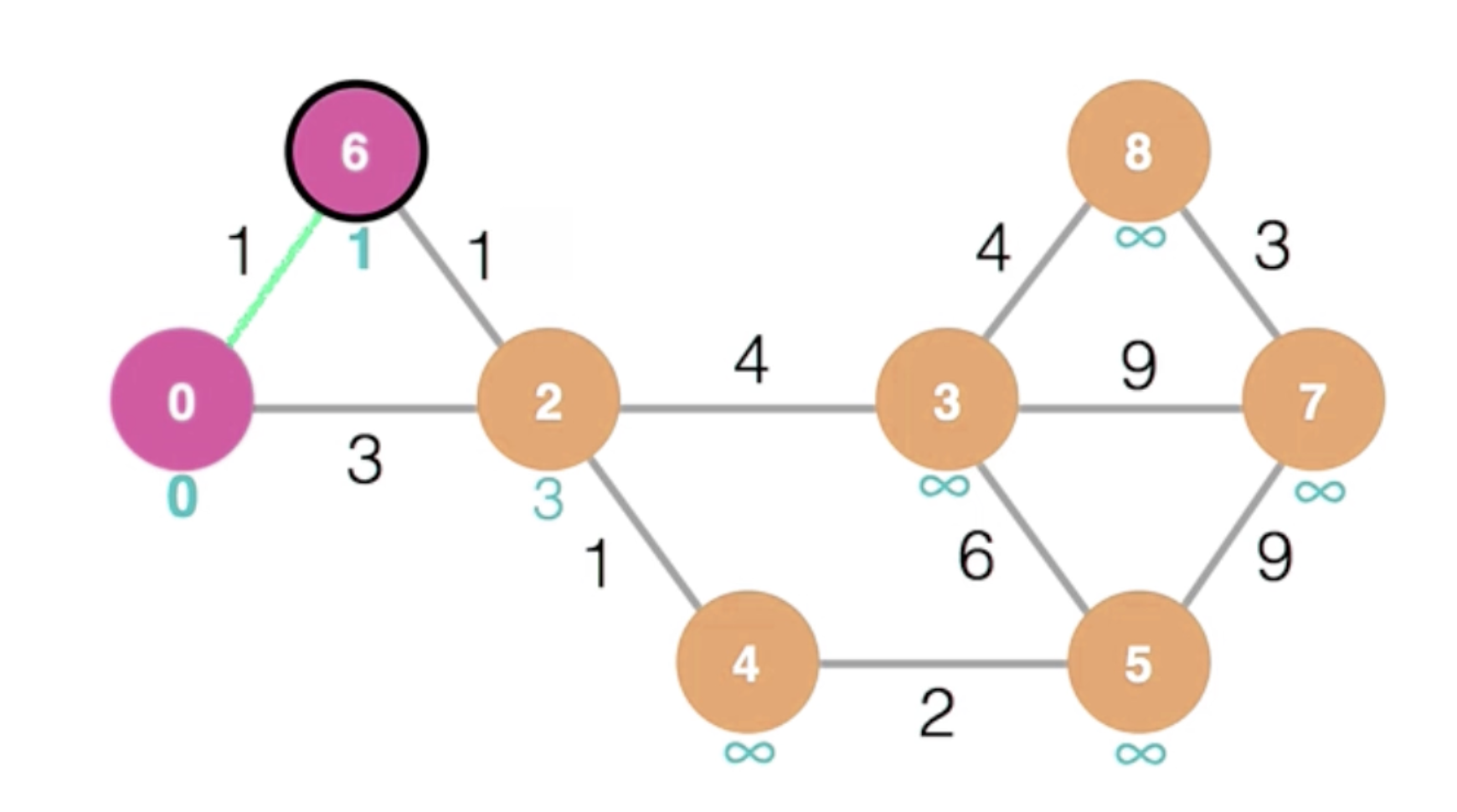
이후 6으로 이동한 뒤, 이웃한 정점들의 최소 경로를 업데이트해준다. 0의 경우 0과 1중 0이 더 작으므로 변화가 없다.
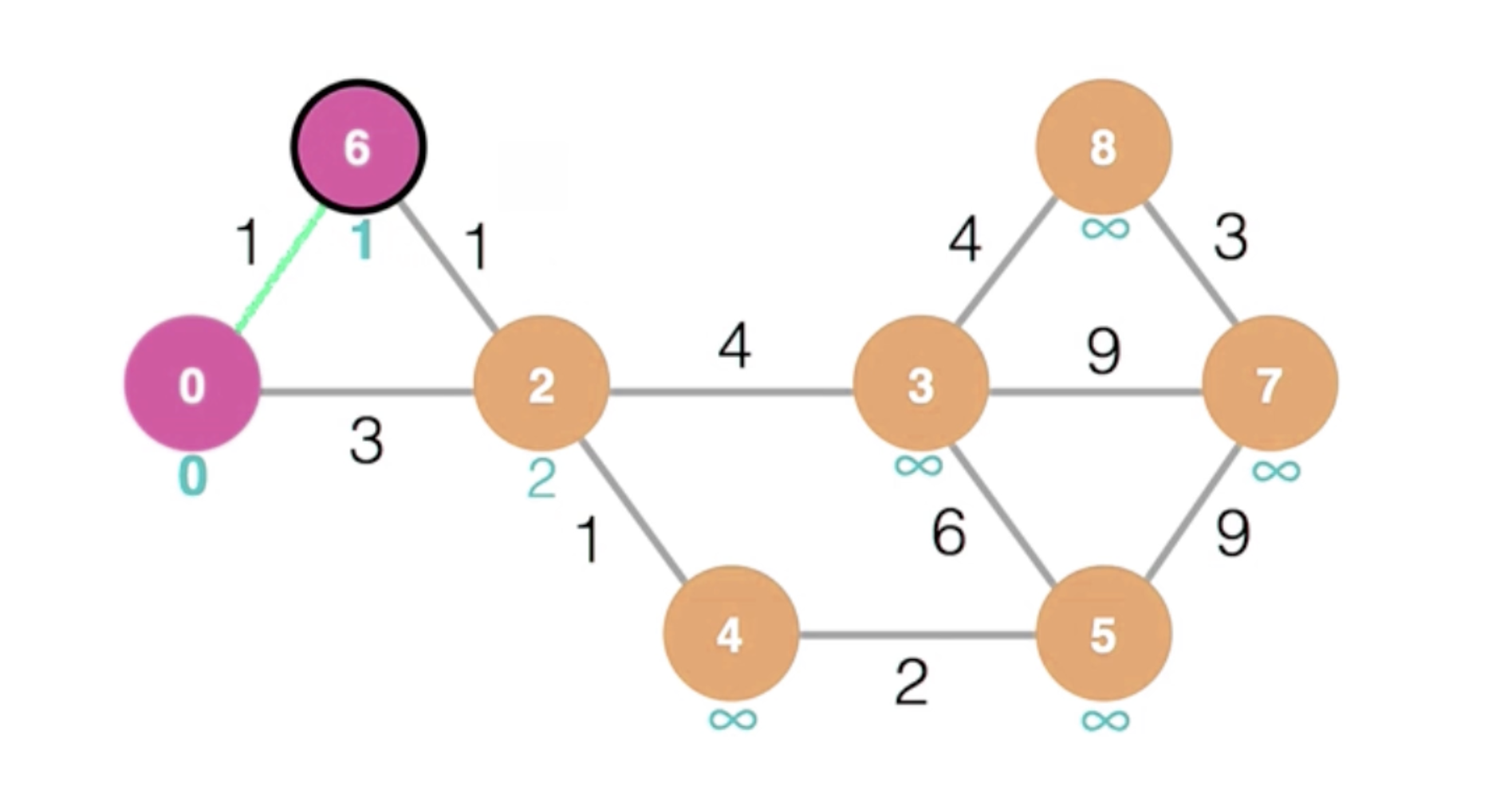
하지만 2의 경우 기존의 3 값보다 1+1 인 2의 값이 더 작기 때문에 2로 업데이트되었다.
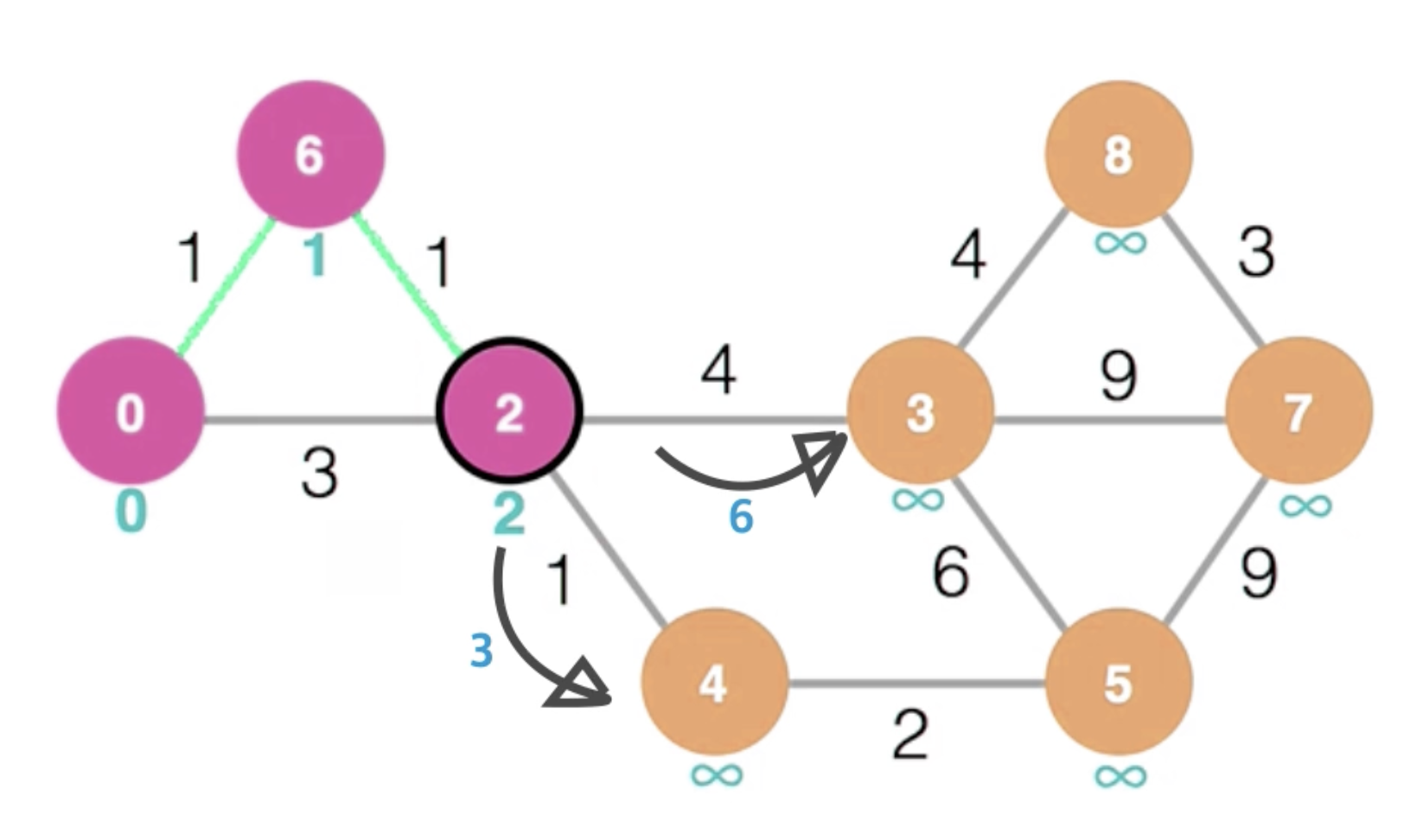
이후 위와 같은 동작을 통해 2의 인접 노드의 값의 업데이트를 시도한다.
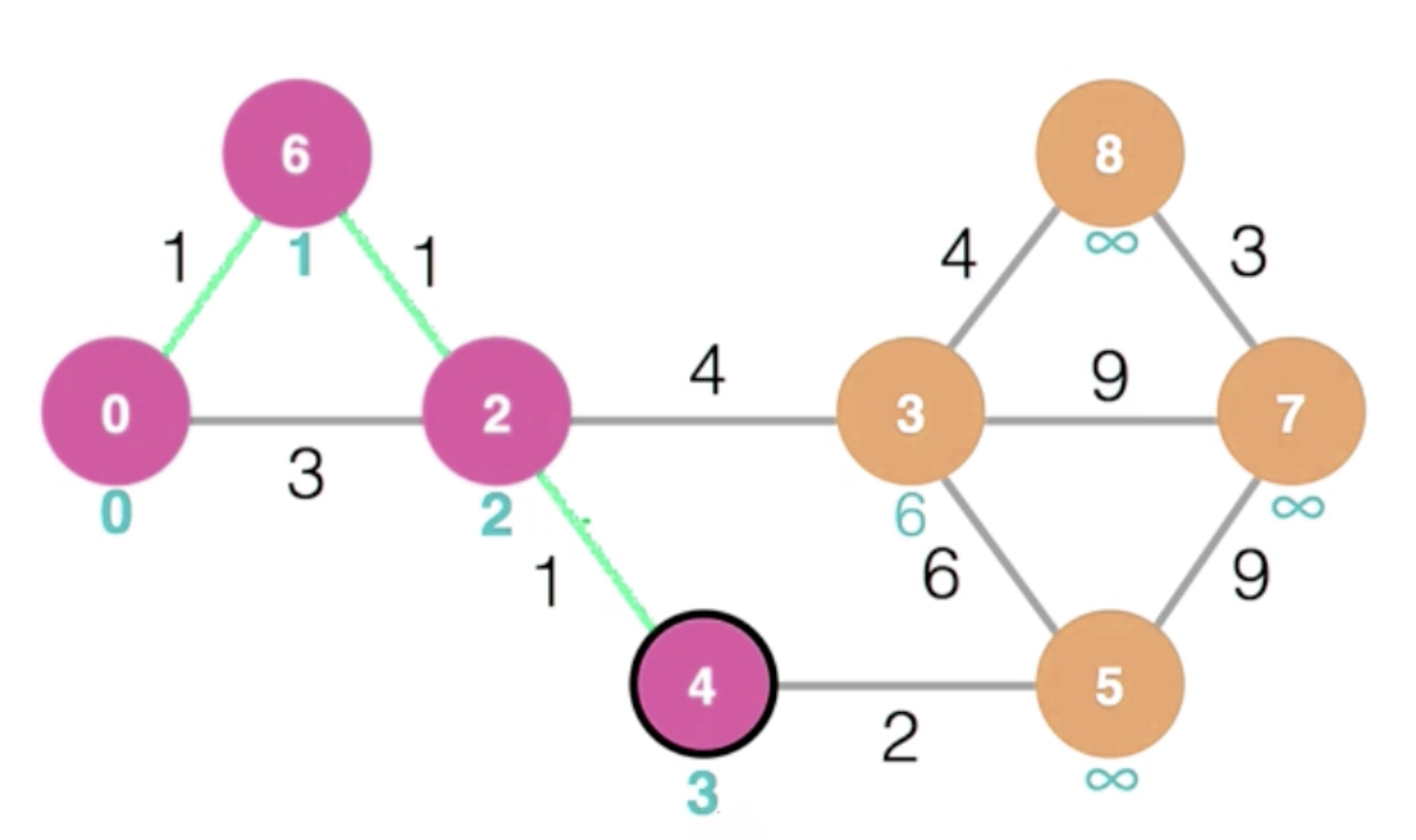
변환된 이후의 값이 저장된다.
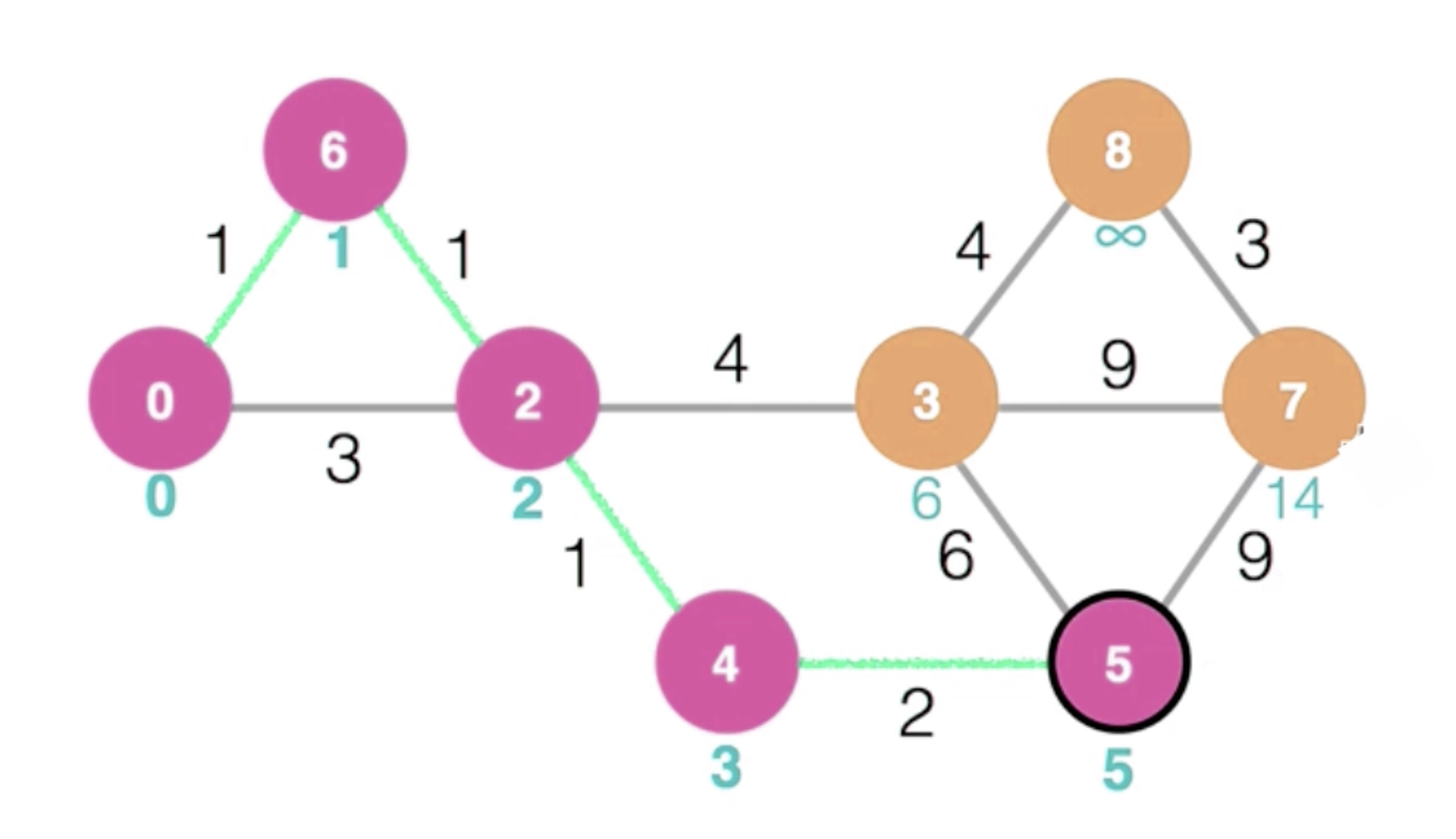
이후 5로 이동하여, 인접한 노드의 최단 경로를 업데이트한다.
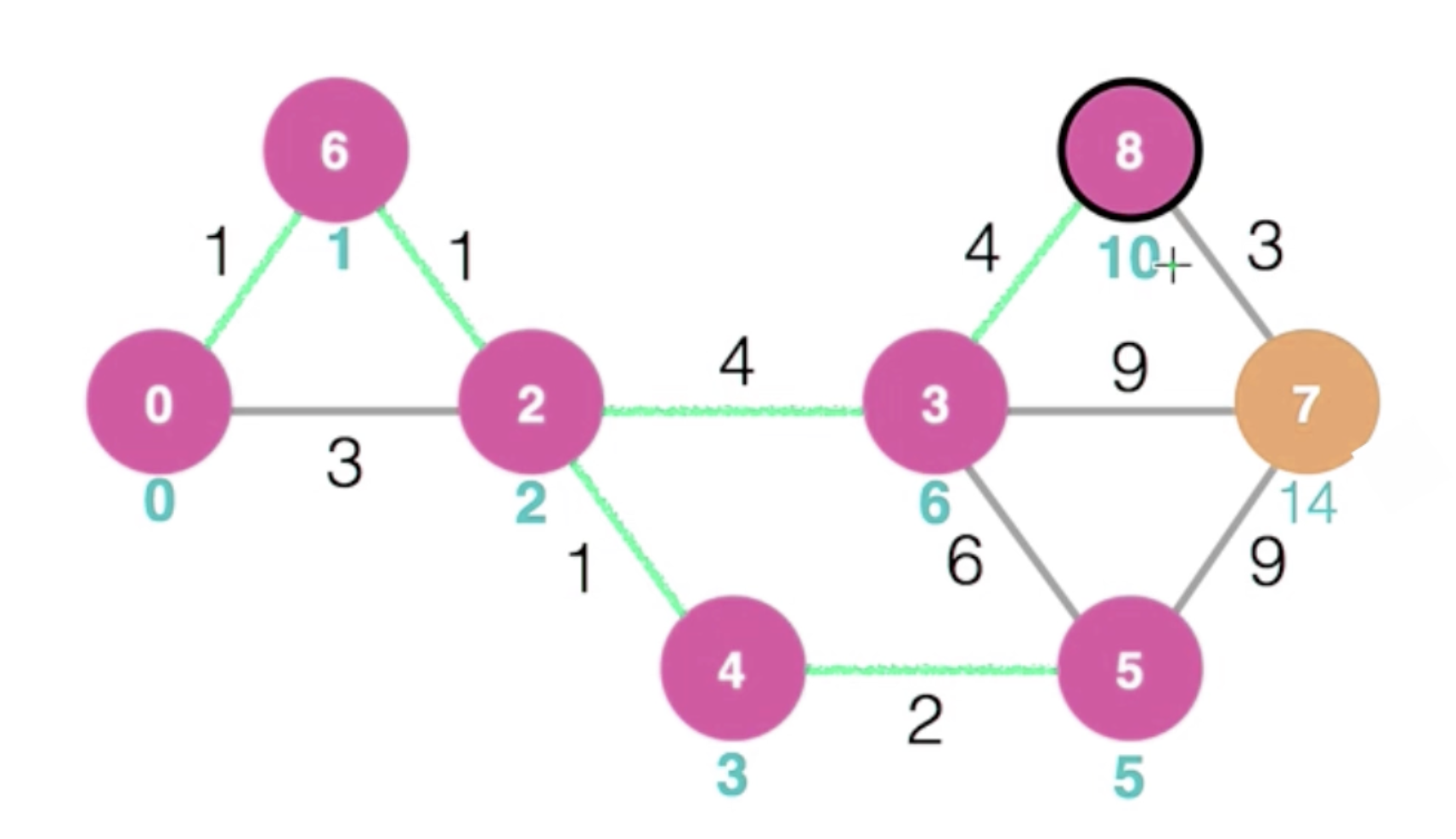
3으로 이동하여 인접한 노드의 최단경로를 업데이트한다.
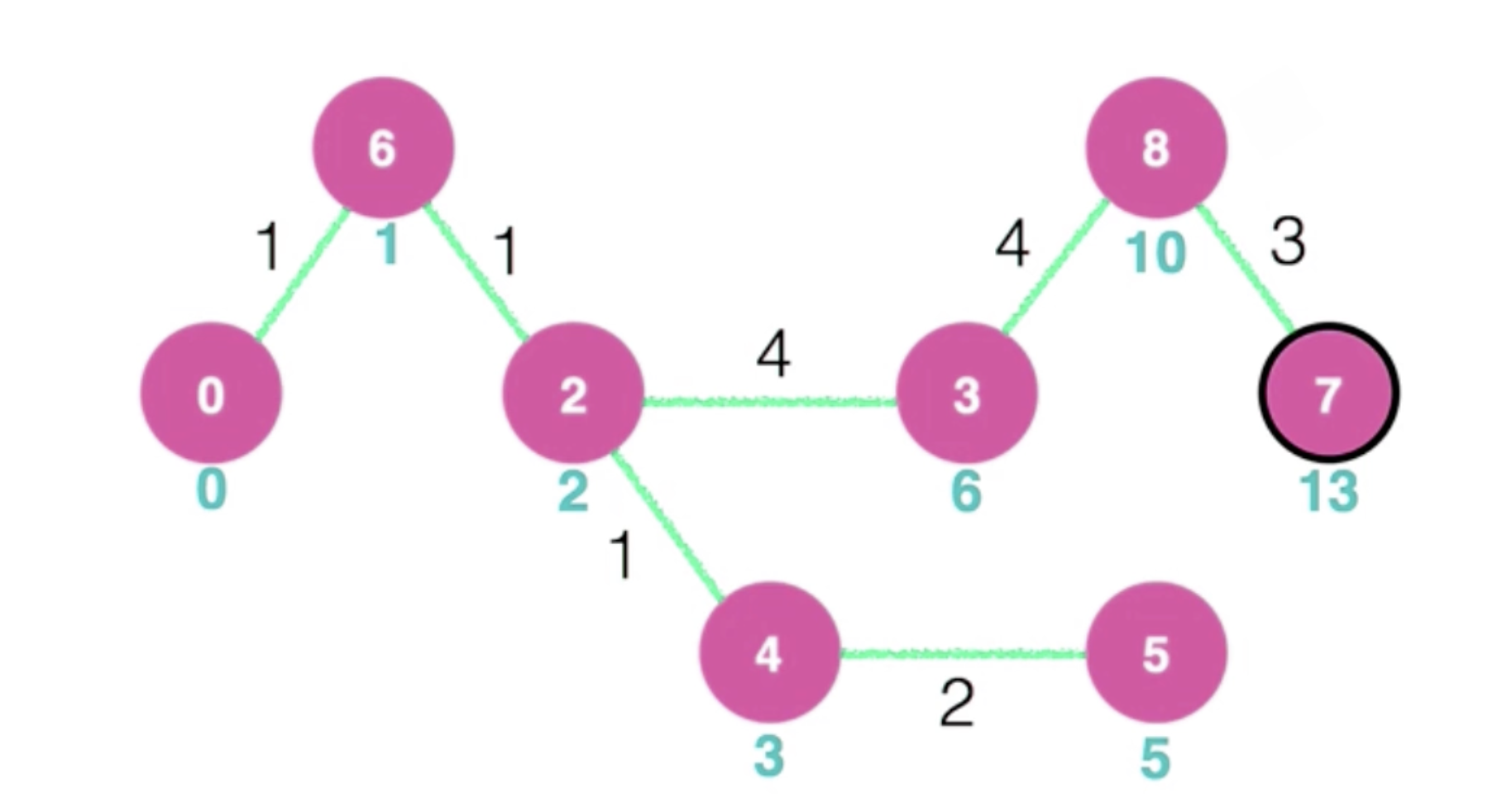
최종 모습이다.
다익스트라 구현하기
이제 위의 설명을 그대로 코드로 구현해보자.
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int start = sc.nextInt();
int end = sc.nextInt();
List<Integer>[] graph = new List[n];
List<Integer>[] cost = new List[n];
int[] table = new int[n];
boolean[] check = new boolean[n];
for (int i = 0; i < graph.length; i++) {
graph[i] = new ArrayList<>();
cost[i] = new ArrayList<>();
}
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
cost[a].add(c);
cost[b].add(c);
}
for (int i = 0; i < n; i++) {
table[i] = Integer.MAX_VALUE;
}
table[start] = 0;
for (int i = 0; i < n; i++) {
int minValue = Integer.MAX_VALUE;
int minIndex = -1;
//최솟값을 구한다. 단, 지금까지 최단거리로 확정되지 않았던 정점에 대해서
for (int j = 0; j < n; j++) {
if (!check[j] && minValue > table[j]) {
minValue = table[j];
minIndex = j;
}
}
check[minIndex] = true;
//그 최솟값을 갖는 노드로 부터 뻗어나간다.
for (int j = 0; j < graph[minIndex].size(); j++) {
int node2 = graph[minIndex].get(j);
int cost2 = cost[minIndex].get(j);
if (table[node2] > table[minIndex] + cost2) {
table[node2] = table[minIndex] + cost2;
}
}
}
System.out.println(table[end]);
}
}코드를 이해하는 것이 어렵다면 아래의 그림의 동작 과정을 다시 한번 살펴보자.
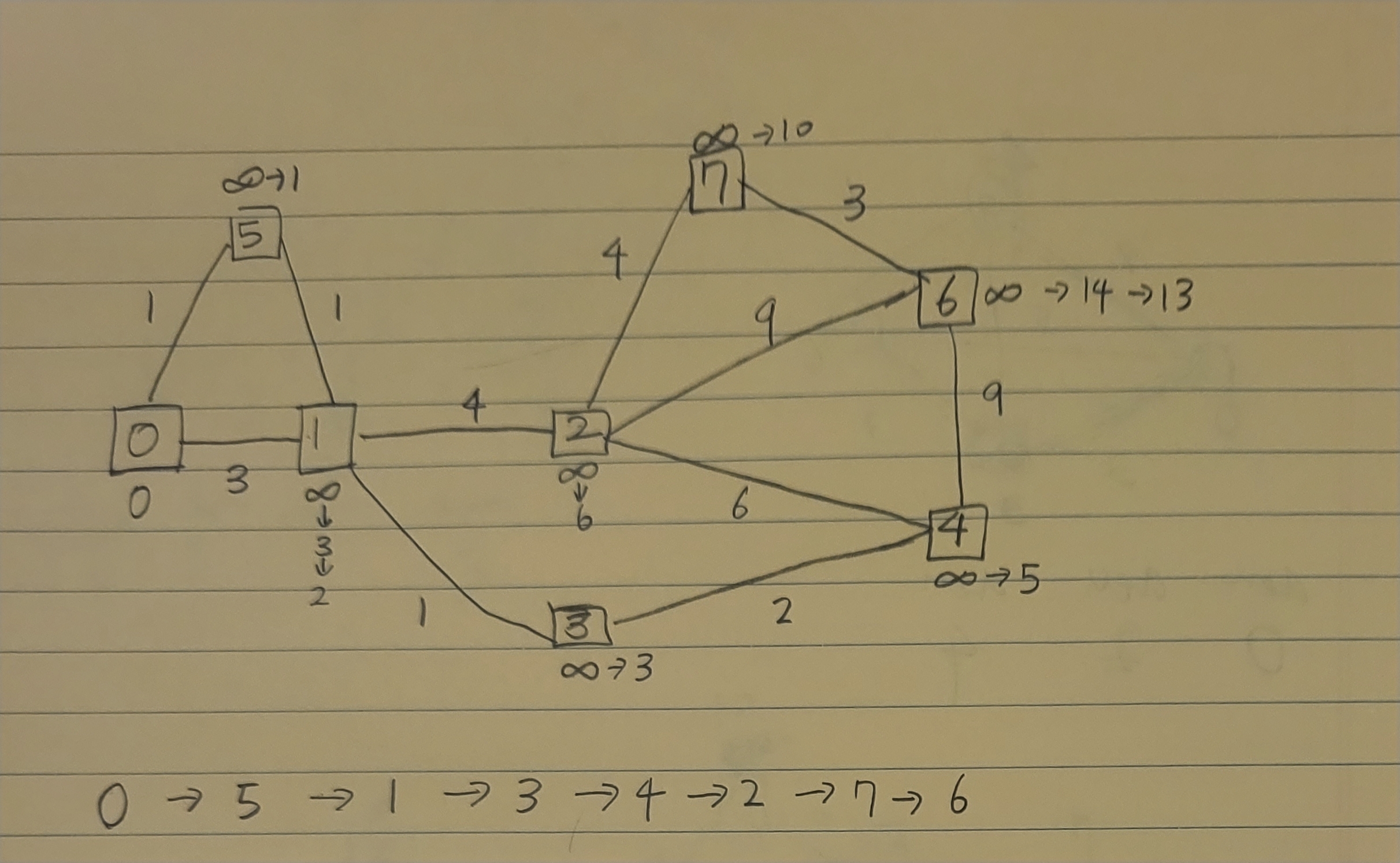
이 그림의 순서대로 동작이 이루어진다.
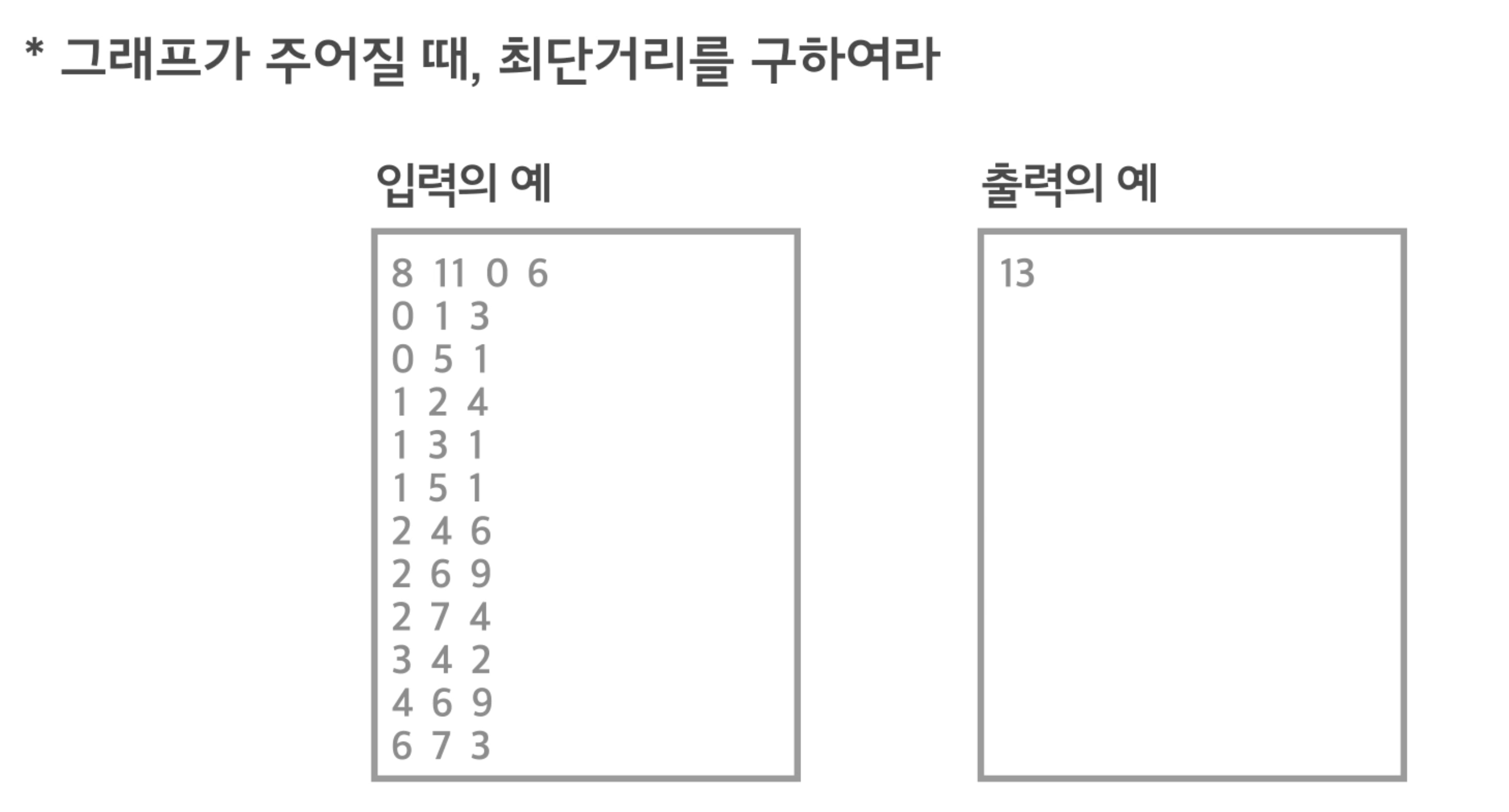
다익스트라 활용 문제를 풀어보자
최단거리
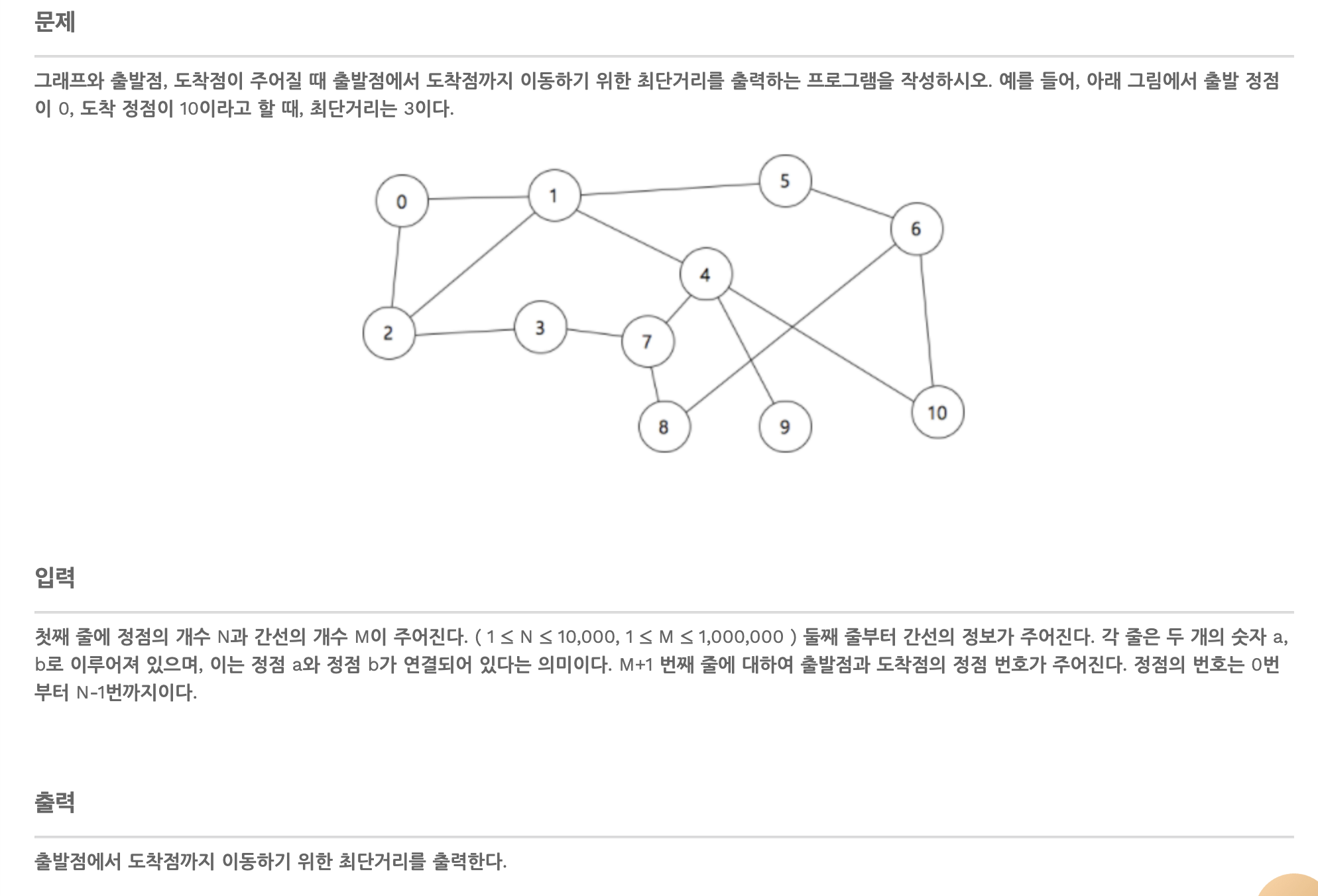
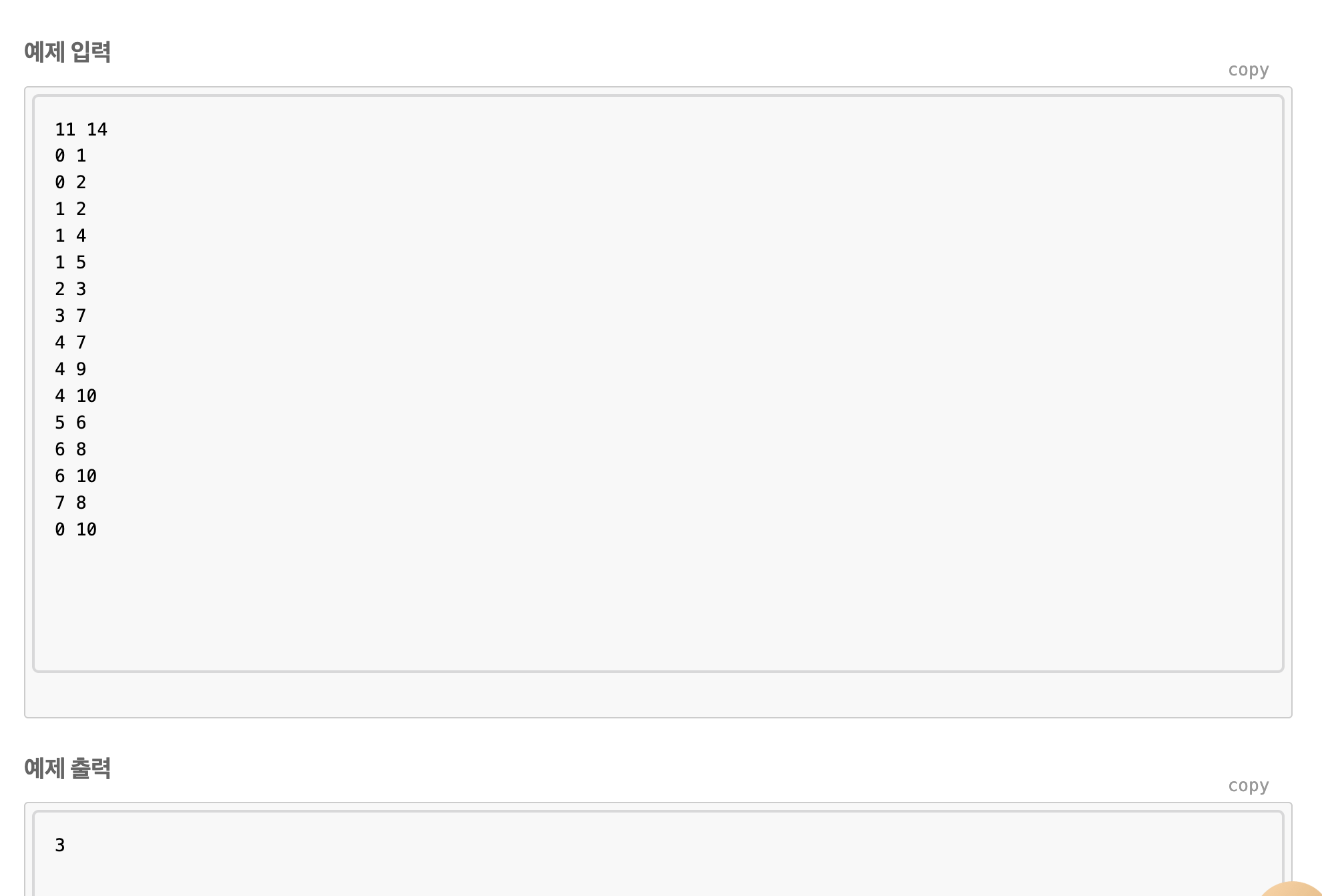
위 문제는 방금 배웠던 다익스트라의 문제에서 가중치가 사라진 문제이다.
쉽게 풀 수 있는 문제이다.
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
List<Integer>[] graph = new List[n];
int[] table = new int[n];
boolean[] check = new boolean[n];
for (int i = 0; i < graph.length; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
}
int start = sc.nextInt();
int end = sc.nextInt();
for (int i = 0; i < n; i++) {
table[i] = Integer.MAX_VALUE;
}
table[start] = 0;
for (int i = 0; i < n; i++) {
int minValue = Integer.MAX_VALUE;
int minIndex = -1;
for (int j = 0; j < n; j++) {
if (!check[j] && minValue > table[j]) {
minValue = table[j];
minIndex = j;
}
}
check[minIndex] = true;
for (int j = 0; j < graph[minIndex].size(); j++) {
int node2 = graph[minIndex].get(j);
if (table[node2] > table[minIndex] +1){
table[node2] = table[minIndex] +1;
}
}
}
System.out.println(table[end]);
}
}특정 최단거리

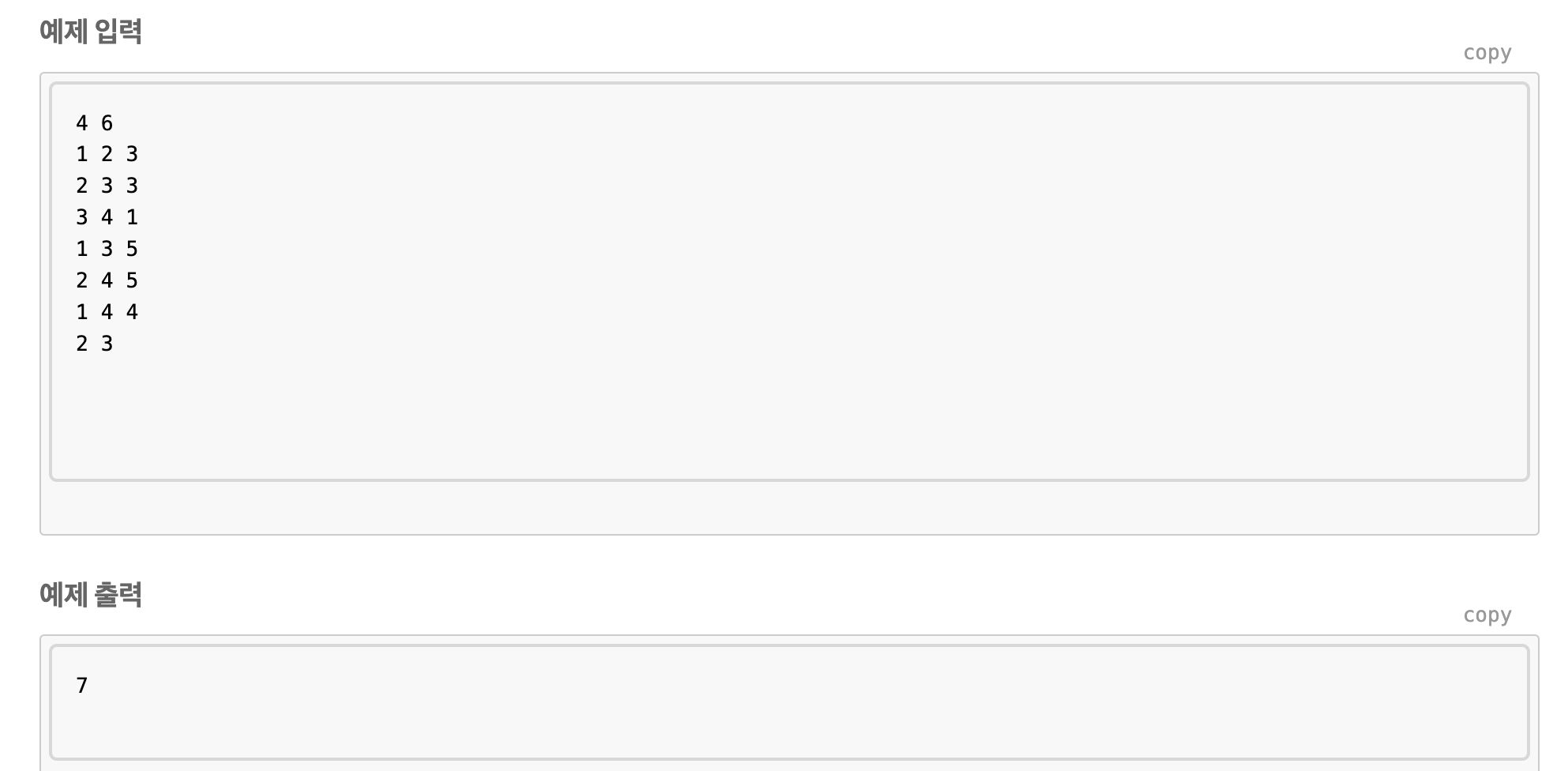
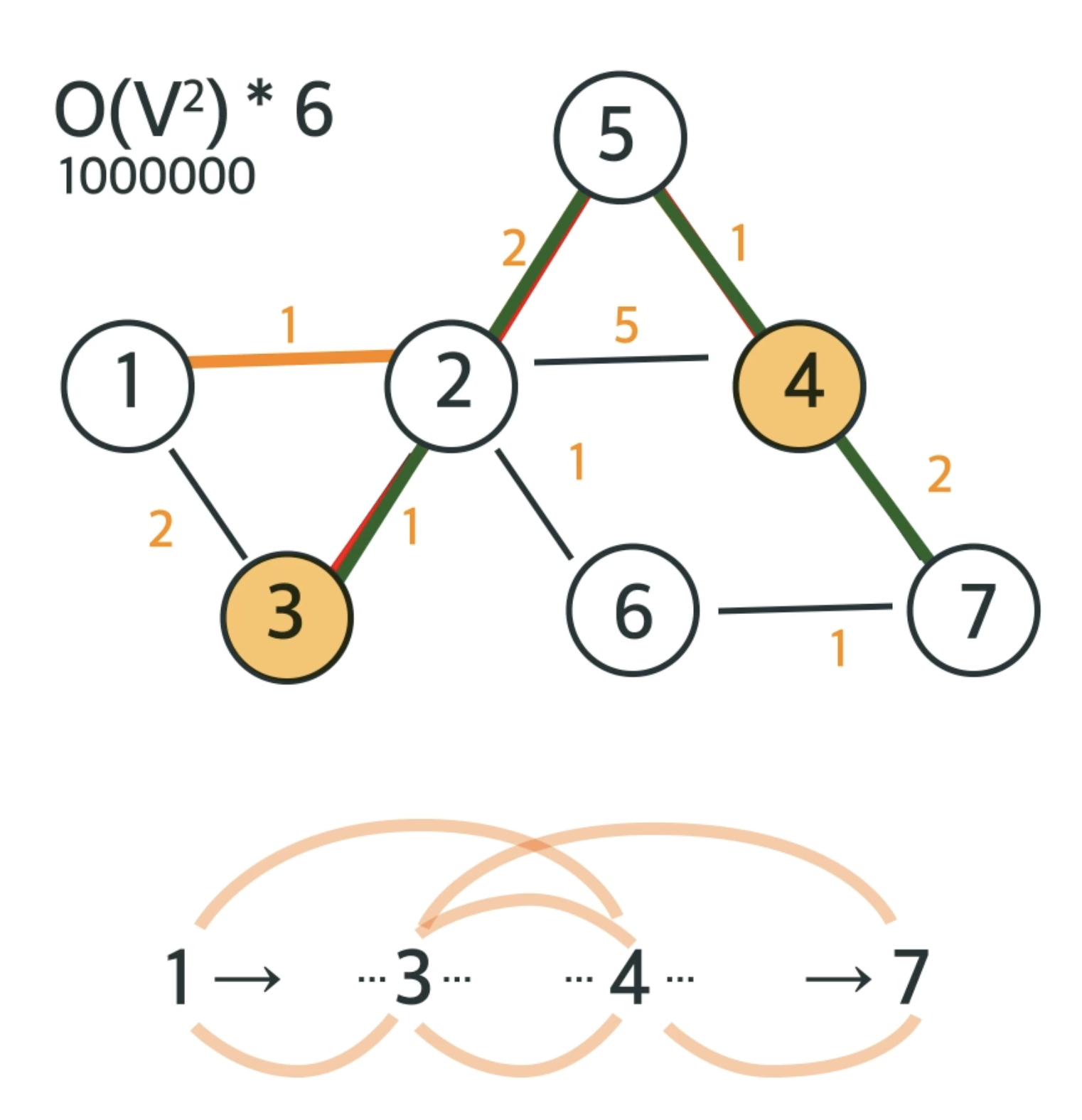
특정한 점을 지나야 한다.
우리는 특정 한 점에서 이동하는 다익스트라만을 이용하여 풀 수 있다.
시작점 - A - B - 끝으로 이동할 수 있다.
하지만 경우에 따라 시작점 - B - A - 끝의 경우가 최단거리가 될 수도 있기 때문에 둘 다 검사해야 한다.
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main0 {
static int n;
static int m;
static int[] table;
static boolean[] check;
static List<Integer>[] graph;
static List<Integer>[] cost;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
graph = new List[n+1];
cost = new List[n+1];
table = new int[n+1];
check = new boolean[n+1];
for (int i = 1; i < graph.length; i++) {
graph[i] = new ArrayList<>();
cost[i] = new ArrayList<>();
}
for (int i = 1; i <= m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
cost[a].add(c);
cost[b].add(c);
}
int A = sc.nextInt();
int B = sc.nextInt();
int first = (getFast(1,A)+getFast(A,B) +getFast(B,n));
int second = (getFast(1,B)+getFast(B,A) +getFast(A,n));
System.out.println(Math.min(first,second));
}
static private int getFast(int start, int end) {
for (int i =1; i<=n; i++)check[i] = false;
for (int i = 1; i <= n; i++)table[i] = Integer.MAX_VALUE;
table[start] = 0;
for (int i = 1; i <= n; i++) {
int minValue = Integer.MAX_VALUE;
int minIndex = -1;
for (int j = 1; j <= n; j++) {
if (!check[j] && minValue > table[j]) {
minValue = table[j];
minIndex = j;
}
}
check[minIndex] = true;
for (int j = 0; j < graph[minIndex].size(); j++) {
int node2 = graph[minIndex].get(j);
int cost2 = cost[minIndex].get(j);
if (table[node2] > table[minIndex] + cost2) {
table[node2] = table[minIndex] + cost2;
}
}
}
return table[end];
}
}
파티

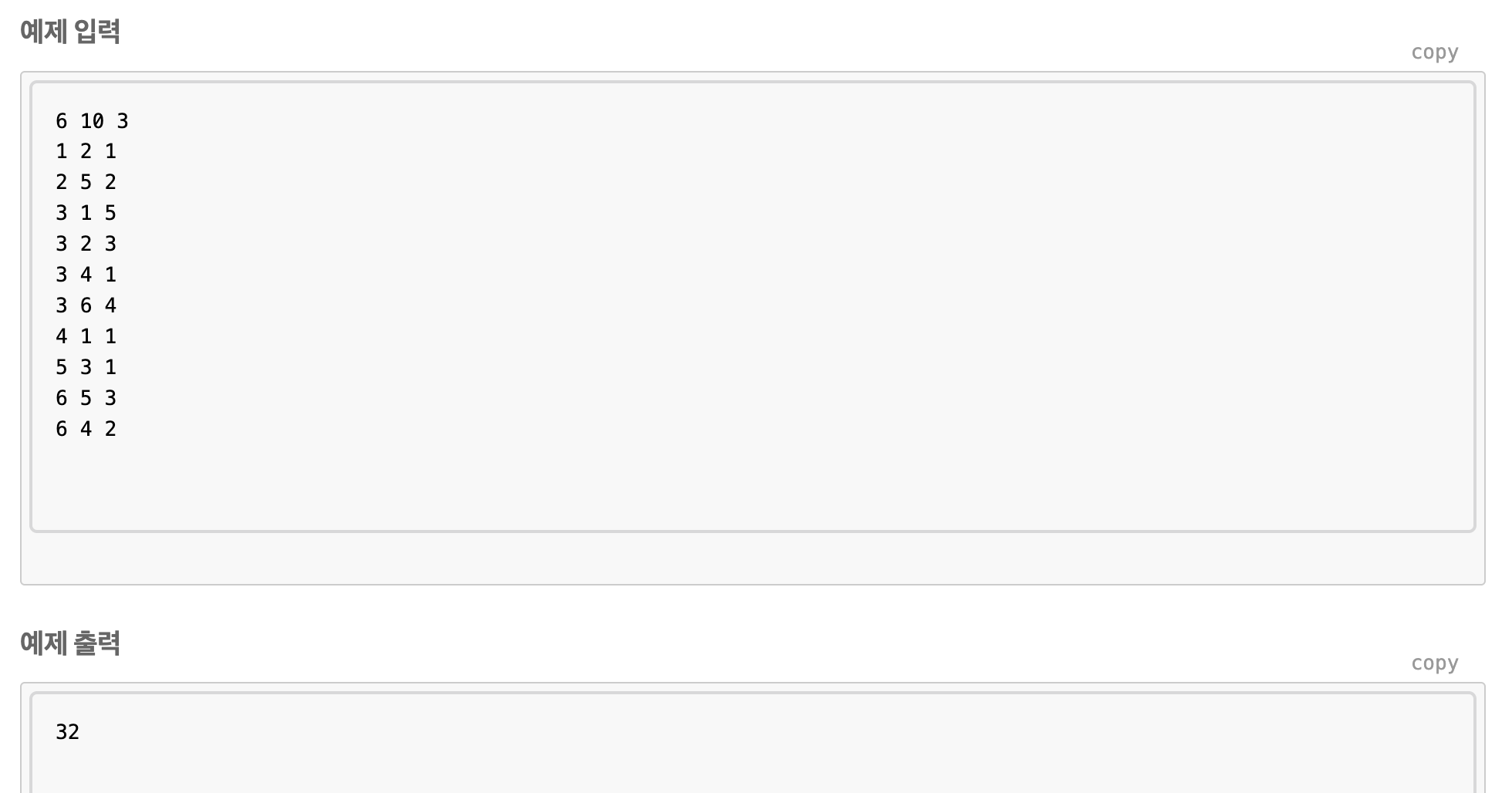
이 문제는 여태까지의 문제와 달리 단방향이다.
또한 다른 지역에서 한 곳으로 모이는 이동거리와 한 지역에서 다른 곳으로 가는 이동거리를 구해야 한다.
다익스트라를 활용하여 한 지역에서 다른 곳으로 가는 이동거리는 쉽게 해결할 수 있지만,
전자의 경우 O(V^2)*V로 풀 수 있다.(1개씩 다익스트라를 적용)
하지만 이 경우에는 너무 많은 시간이 걸리게 된다.
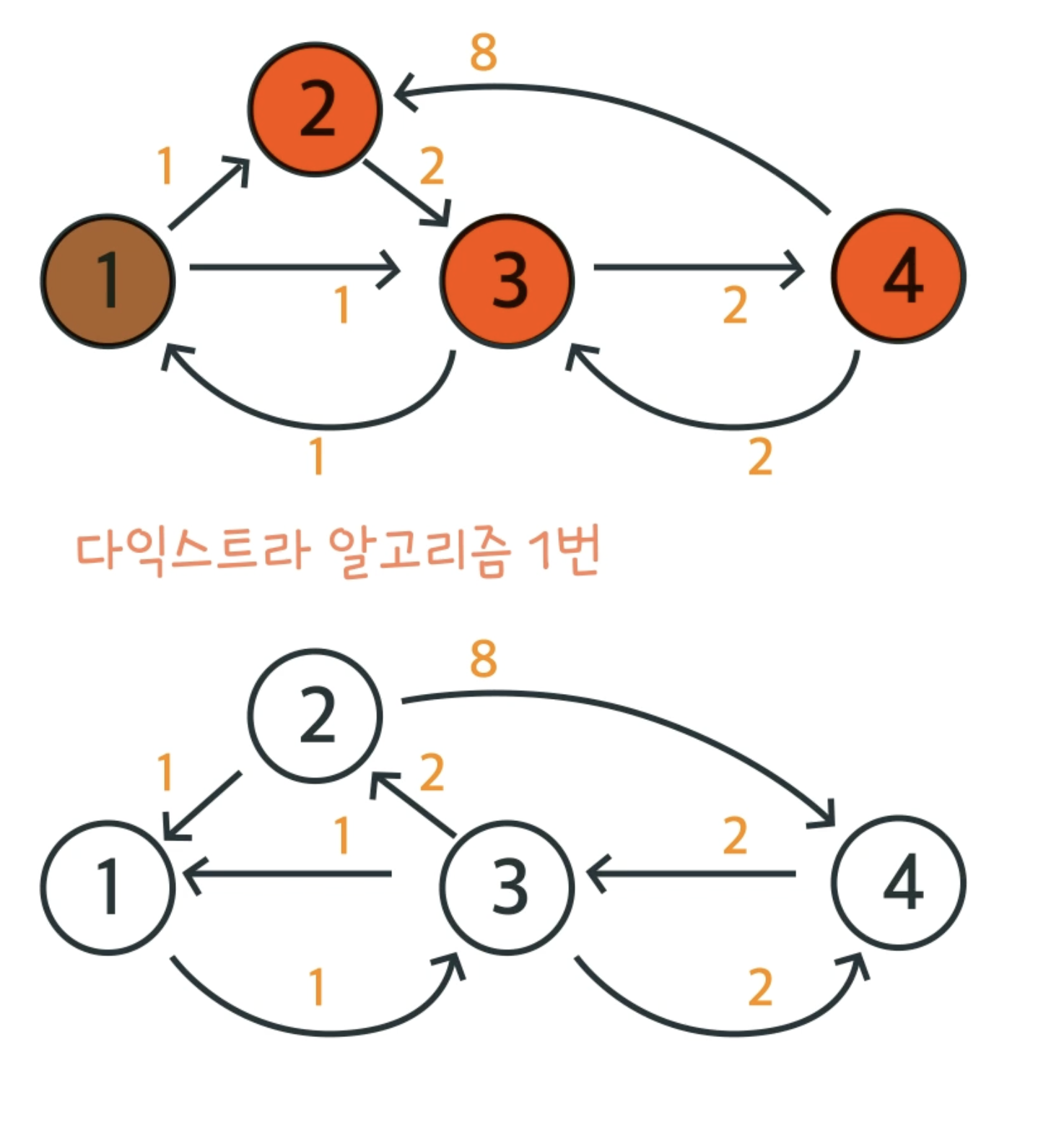
따라서 방향을 반대로 바꾸어 되돌아가는 경우로 생각을 한다면 다익스트라를 1번만 사용해서 풀 수 있다.
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
static int n;
static int m;
static int[] table;
static boolean[] check;
static List<Integer>[] graph;
static List<Integer>[] cost;
static List<Integer>[] reverseGraph;
static List<Integer>[] reverseCost;
static int destination;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
destination = sc.nextInt();
graph = new List[n+1];
reverseGraph = new List[n+1];
cost = new List[n+1];
reverseCost = new List[n+1];
table = new int[n+1];
check = new boolean[n+1];
for (int i = 1; i < graph.length; i++) {
graph[i] = new ArrayList<>();
reverseGraph[i] = new ArrayList<>();
cost[i] = new ArrayList<>();
reverseCost[i] = new ArrayList<>();
}
for (int i = 1; i <= m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
graph[a].add(b);
reverseGraph[b].add(a);
cost[a].add(c);
reverseCost[b].add(c);
}
System.out.println(getBye(destination) + getCome(destination));
}
static private int getCome(int start) {
for (int i =1; i<=n; i++)check[i] = false;
for (int i = 1; i <= n; i++)table[i] = Integer.MAX_VALUE;
table[start] = 0;
for (int i = 1; i <= n; i++) {
int minValue = Integer.MAX_VALUE;
int minIndex = -1;
for (int j = 1; j <= n; j++) {
if (!check[j] && minValue > table[j]) {
minValue = table[j];
minIndex = j;
}
}
check[minIndex] = true;
for (int j = 0; j < graph[minIndex].size(); j++) {
int node2 = graph[minIndex].get(j);
int cost2 = cost[minIndex].get(j);
if (table[node2] > table[minIndex] + cost2) {
table[node2] = table[minIndex] + cost2;
}
}
}
int sum=0;
for (int i=1;i<=n;i++){
sum+=table[i];
}
return sum;
}
static private int getBye(int start) {
for (int i =1; i<=n; i++)check[i] = false;
for (int i = 1; i <= n; i++)table[i] = Integer.MAX_VALUE;
table[start] = 0;
for (int i = 1; i <= n; i++) {
int minValue = Integer.MAX_VALUE;
int minIndex = -1;
for (int j = 1; j <= n; j++) {
if (!check[j] && minValue > table[j]) {
minValue = table[j];
minIndex = j;
}
}
check[minIndex] = true;
for (int j = 0; j < reverseGraph[minIndex].size(); j++) {
int node2 = reverseGraph[minIndex].get(j);
int cost2 = reverseCost[minIndex].get(j);
if (table[node2] > table[minIndex] + cost2) {
table[node2] = table[minIndex] + cost2;
}
}
}
int sum = 0;
for (int i =1; i<=n;i++){
sum+=table[i];
}
return sum;
}
}
배운 점
처음에 다익스트라를 쉽게 이해하지 못하였다.
그래서 구현만 5번은 넘게 했던 것 같다.
이러한 과정이 이해하고 적용하는데 큰 도움이 된 것 같다.
다익스트라를 활용하면, 단순하게 문제를 푸는 것이 아닌 개발을 할 때에도 큰 도움이 될 것 같다는 생각을 하였다.
나중에 개인 프로젝트를 만들어볼 때, 다익스트라를 활용해보아야겠다.
'PS > 알고리즘' 카테고리의 다른 글
| 비트마스크(BitMask) (2) | 2023.01.20 |
|---|---|
| 동적계획법(DP) (2) | 2022.12.20 |
| 너비 우선 탐색(BFS) (1) | 2022.11.14 |
| 깊이 우선 탐색(DFS) (2) | 2022.11.06 |
| 자료구조(Graph) (2) | 2022.11.02 |
그래프를 활용하여 최단 경로를 구할 수는 없을까?
최단경로 알고리즘은 크게 3가지가 존재한다.

이번 시간에는 다익스트라만 다루도록 하겠다.
다익스트라란?
음의 가중치가 없는 그래프의 한 정점에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘이다.

정점 사이에는 가중치가 존재한다.
최단경로의 특징
정점 x까지 최단거리로 가기 위해서는 그 직전까지도 최단거리로 가야 한다.
위의 그림을 보면 1 - 6 - 2 - 3 - 8 - 7 순으로 이동한다.
최단경로의 특징을 이용하면 1~8까지 이동할 때에도 최단 경로로 이동한다.
그래서 최단경로 트리를 어떻게 만들 것인가?
T(i) = i까지 도달하는 최단거리 -> 파란색 숫자
순서를 그림을 이용하여 천천히 설명하겠다.
보라 색원은 이미 탐색을 완료했다는 의미이다.

처음 시작점을 0으로 두고 나머지는 무한대로 설정한다.

인접한 노드의 거리를 설정한다.

이후 6으로 이동한 뒤, 이웃한 정점들의 최소 경로를 업데이트해준다. 0의 경우 0과 1중 0이 더 작으므로 변화가 없다.

하지만 2의 경우 기존의 3 값보다 1+1 인 2의 값이 더 작기 때문에 2로 업데이트되었다.

이후 위와 같은 동작을 통해 2의 인접 노드의 값의 업데이트를 시도한다.

변환된 이후의 값이 저장된다.

이후 5로 이동하여, 인접한 노드의 최단 경로를 업데이트한다.

3으로 이동하여 인접한 노드의 최단경로를 업데이트한다.

최종 모습이다.
다익스트라 구현하기
이제 위의 설명을 그대로 코드로 구현해보자.

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int start = sc.nextInt();
int end = sc.nextInt();
List<Integer>[] graph = new List[n];
List<Integer>[] cost = new List[n];
int[] table = new int[n];
boolean[] check = new boolean[n];
for (int i = 0; i < graph.length; i++) {
graph[i] = new ArrayList<>();
cost[i] = new ArrayList<>();
}
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
cost[a].add(c);
cost[b].add(c);
}
for (int i = 0; i < n; i++) {
table[i] = Integer.MAX_VALUE;
}
table[start] = 0;
for (int i = 0; i < n; i++) {
int minValue = Integer.MAX_VALUE;
int minIndex = -1;
//최솟값을 구한다. 단, 지금까지 최단거리로 확정되지 않았던 정점에 대해서
for (int j = 0; j < n; j++) {
if (!check[j] && minValue > table[j]) {
minValue = table[j];
minIndex = j;
}
}
check[minIndex] = true;
//그 최솟값을 갖는 노드로 부터 뻗어나간다.
for (int j = 0; j < graph[minIndex].size(); j++) {
int node2 = graph[minIndex].get(j);
int cost2 = cost[minIndex].get(j);
if (table[node2] > table[minIndex] + cost2) {
table[node2] = table[minIndex] + cost2;
}
}
}
System.out.println(table[end]);
}
}코드를 이해하는 것이 어렵다면 아래의 그림의 동작 과정을 다시 한번 살펴보자.

이 그림의 순서대로 동작이 이루어진다.
다익스트라 활용 문제를 풀어보자
최단거리


위 문제는 방금 배웠던 다익스트라의 문제에서 가중치가 사라진 문제이다.
쉽게 풀 수 있는 문제이다.
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
List<Integer>[] graph = new List[n];
int[] table = new int[n];
boolean[] check = new boolean[n];
for (int i = 0; i < graph.length; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
}
int start = sc.nextInt();
int end = sc.nextInt();
for (int i = 0; i < n; i++) {
table[i] = Integer.MAX_VALUE;
}
table[start] = 0;
for (int i = 0; i < n; i++) {
int minValue = Integer.MAX_VALUE;
int minIndex = -1;
for (int j = 0; j < n; j++) {
if (!check[j] && minValue > table[j]) {
minValue = table[j];
minIndex = j;
}
}
check[minIndex] = true;
for (int j = 0; j < graph[minIndex].size(); j++) {
int node2 = graph[minIndex].get(j);
if (table[node2] > table[minIndex] +1){
table[node2] = table[minIndex] +1;
}
}
}
System.out.println(table[end]);
}
}특정 최단거리


특정한 점을 지나야 한다.
우리는 특정 한 점에서 이동하는 다익스트라만을 이용하여 풀 수 있다.
시작점 - A - B - 끝으로 이동할 수 있다.
하지만 경우에 따라 시작점 - B - A - 끝의 경우가 최단거리가 될 수도 있기 때문에 둘 다 검사해야 한다.

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main0 {
static int n;
static int m;
static int[] table;
static boolean[] check;
static List<Integer>[] graph;
static List<Integer>[] cost;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
graph = new List[n+1];
cost = new List[n+1];
table = new int[n+1];
check = new boolean[n+1];
for (int i = 1; i < graph.length; i++) {
graph[i] = new ArrayList<>();
cost[i] = new ArrayList<>();
}
for (int i = 1; i <= m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
cost[a].add(c);
cost[b].add(c);
}
int A = sc.nextInt();
int B = sc.nextInt();
int first = (getFast(1,A)+getFast(A,B) +getFast(B,n));
int second = (getFast(1,B)+getFast(B,A) +getFast(A,n));
System.out.println(Math.min(first,second));
}
static private int getFast(int start, int end) {
for (int i =1; i<=n; i++)check[i] = false;
for (int i = 1; i <= n; i++)table[i] = Integer.MAX_VALUE;
table[start] = 0;
for (int i = 1; i <= n; i++) {
int minValue = Integer.MAX_VALUE;
int minIndex = -1;
for (int j = 1; j <= n; j++) {
if (!check[j] && minValue > table[j]) {
minValue = table[j];
minIndex = j;
}
}
check[minIndex] = true;
for (int j = 0; j < graph[minIndex].size(); j++) {
int node2 = graph[minIndex].get(j);
int cost2 = cost[minIndex].get(j);
if (table[node2] > table[minIndex] + cost2) {
table[node2] = table[minIndex] + cost2;
}
}
}
return table[end];
}
}
파티


이 문제는 여태까지의 문제와 달리 단방향이다.
또한 다른 지역에서 한 곳으로 모이는 이동거리와 한 지역에서 다른 곳으로 가는 이동거리를 구해야 한다.
다익스트라를 활용하여 한 지역에서 다른 곳으로 가는 이동거리는 쉽게 해결할 수 있지만,
전자의 경우 O(V^2)*V로 풀 수 있다.(1개씩 다익스트라를 적용)
하지만 이 경우에는 너무 많은 시간이 걸리게 된다.
따라서 방향을 반대로 바꾸어 되돌아가는 경우로 생각을 한다면 다익스트라를 1번만 사용해서 풀 수 있다.

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
static int n;
static int m;
static int[] table;
static boolean[] check;
static List<Integer>[] graph;
static List<Integer>[] cost;
static List<Integer>[] reverseGraph;
static List<Integer>[] reverseCost;
static int destination;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
destination = sc.nextInt();
graph = new List[n+1];
reverseGraph = new List[n+1];
cost = new List[n+1];
reverseCost = new List[n+1];
table = new int[n+1];
check = new boolean[n+1];
for (int i = 1; i < graph.length; i++) {
graph[i] = new ArrayList<>();
reverseGraph[i] = new ArrayList<>();
cost[i] = new ArrayList<>();
reverseCost[i] = new ArrayList<>();
}
for (int i = 1; i <= m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
graph[a].add(b);
reverseGraph[b].add(a);
cost[a].add(c);
reverseCost[b].add(c);
}
System.out.println(getBye(destination) + getCome(destination));
}
static private int getCome(int start) {
for (int i =1; i<=n; i++)check[i] = false;
for (int i = 1; i <= n; i++)table[i] = Integer.MAX_VALUE;
table[start] = 0;
for (int i = 1; i <= n; i++) {
int minValue = Integer.MAX_VALUE;
int minIndex = -1;
for (int j = 1; j <= n; j++) {
if (!check[j] && minValue > table[j]) {
minValue = table[j];
minIndex = j;
}
}
check[minIndex] = true;
for (int j = 0; j < graph[minIndex].size(); j++) {
int node2 = graph[minIndex].get(j);
int cost2 = cost[minIndex].get(j);
if (table[node2] > table[minIndex] + cost2) {
table[node2] = table[minIndex] + cost2;
}
}
}
int sum=0;
for (int i=1;i<=n;i++){
sum+=table[i];
}
return sum;
}
static private int getBye(int start) {
for (int i =1; i<=n; i++)check[i] = false;
for (int i = 1; i <= n; i++)table[i] = Integer.MAX_VALUE;
table[start] = 0;
for (int i = 1; i <= n; i++) {
int minValue = Integer.MAX_VALUE;
int minIndex = -1;
for (int j = 1; j <= n; j++) {
if (!check[j] && minValue > table[j]) {
minValue = table[j];
minIndex = j;
}
}
check[minIndex] = true;
for (int j = 0; j < reverseGraph[minIndex].size(); j++) {
int node2 = reverseGraph[minIndex].get(j);
int cost2 = reverseCost[minIndex].get(j);
if (table[node2] > table[minIndex] + cost2) {
table[node2] = table[minIndex] + cost2;
}
}
}
int sum = 0;
for (int i =1; i<=n;i++){
sum+=table[i];
}
return sum;
}
}
배운 점
처음에 다익스트라를 쉽게 이해하지 못하였다.
그래서 구현만 5번은 넘게 했던 것 같다.
이러한 과정이 이해하고 적용하는데 큰 도움이 된 것 같다.
다익스트라를 활용하면, 단순하게 문제를 푸는 것이 아닌 개발을 할 때에도 큰 도움이 될 것 같다는 생각을 하였다.
나중에 개인 프로젝트를 만들어볼 때, 다익스트라를 활용해보아야겠다.
'PS > 알고리즘' 카테고리의 다른 글
| 비트마스크(BitMask) (2) | 2023.01.20 |
|---|---|
| 동적계획법(DP) (2) | 2022.12.20 |
| 너비 우선 탐색(BFS) (1) | 2022.11.14 |
| 깊이 우선 탐색(DFS) (2) | 2022.11.06 |
| 자료구조(Graph) (2) | 2022.11.02 |
