동적 계획법(Dynamic Proframming)이란?
부분 문제를 해결한 결과를 이용하여 전체 문제를 해결하는 것
작은 나를 해결함으로써 더 큰 나를 해결함
동적 계획법의 문제 풀이 순서
1. 부분 문제를 정의한다.
- 무슨 값을 구할지를 정의한다.
2. 점화식을 구한다.
- 그 값을 어떻게 구할지에 대한 식을 세운다.
( 부분은 풀려있다고 가정)
3. 문제를 해결한다.
- 값을 직접 구하는 코드를 작성한다.
동적 계획법을 활용한 대표적인 예시
피보나치 수 구하기가 있다.

점화식을 활용하기 위해 index 0,1에 해당하는 값을 미리 채워주어야 한다.
반복문을 통해 이전의 값을 활용하여 채워주면서 나아가면 된다.
동적 계획법 활용 문제
개인적으로 동적 계획법 자체는 쉽지만 부분 문제를 정의하는 것이 어렵다고 생각한다.
많은 문제를 풀며 익히는 것이 중요한 것 같다.
직사각형 배치의 경우의 수

문제풀이의 순서에 맞게 풀어보자
1. 부분 문제를 정의한다. -> T(i) = 2* i의 상자를 채우는 경우의 수
2. 점화식 구하기 -> T(i) = T(i-1) + T(i-2) == 피보나치수열
3. 문제를 해결하기
어떻게 저런 식이 나왔는가?
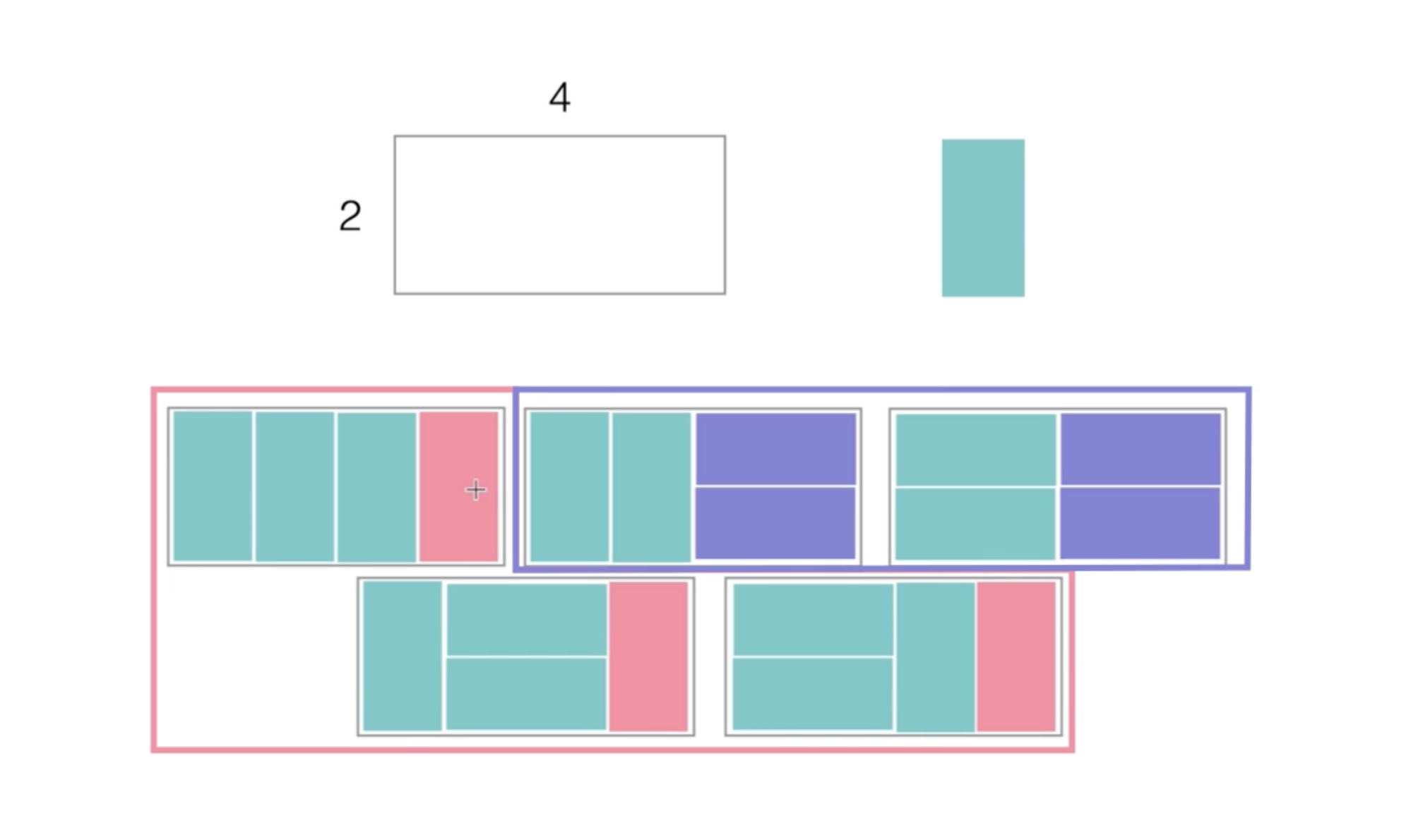
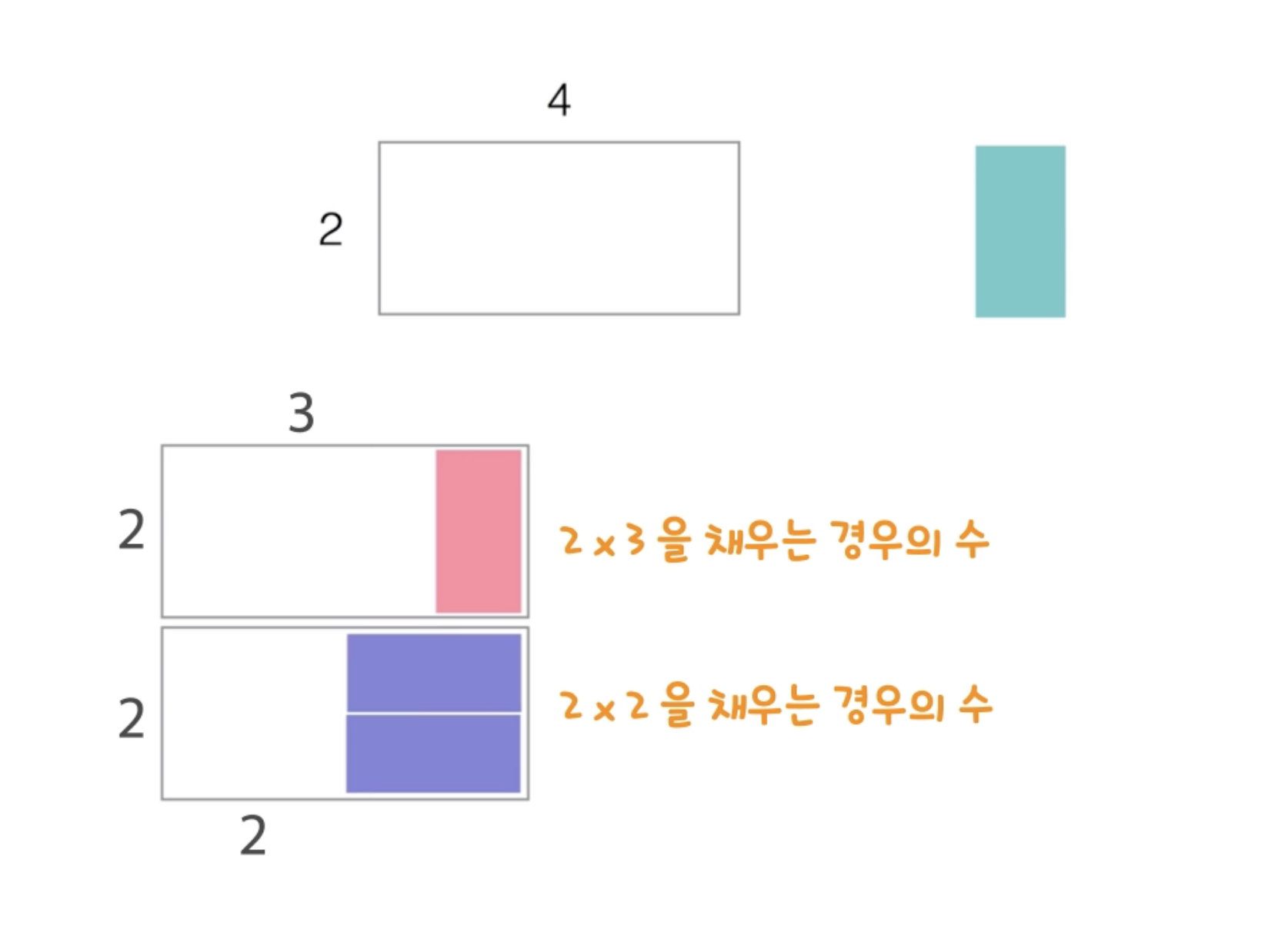
누적 합을 이용하는 문제이다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] rectangle = new int[n+1];
rectangle[1] = 1;
rectangle[2] = 2;
for (int i = 3; i < rectangle.length; i++) {
rectangle[i] = (rectangle[i - 1] + rectangle[i - 2])%1000007;
}
System.out.println(rectangle[n]);
}
}
숫자 만들기

문제풀이의 순서에 맞게 풀어보자
1. 부분 문제를 정의한다. -> T(i) = 1 ~ M의 수를 이용하여 i를 만드는 경우의 수
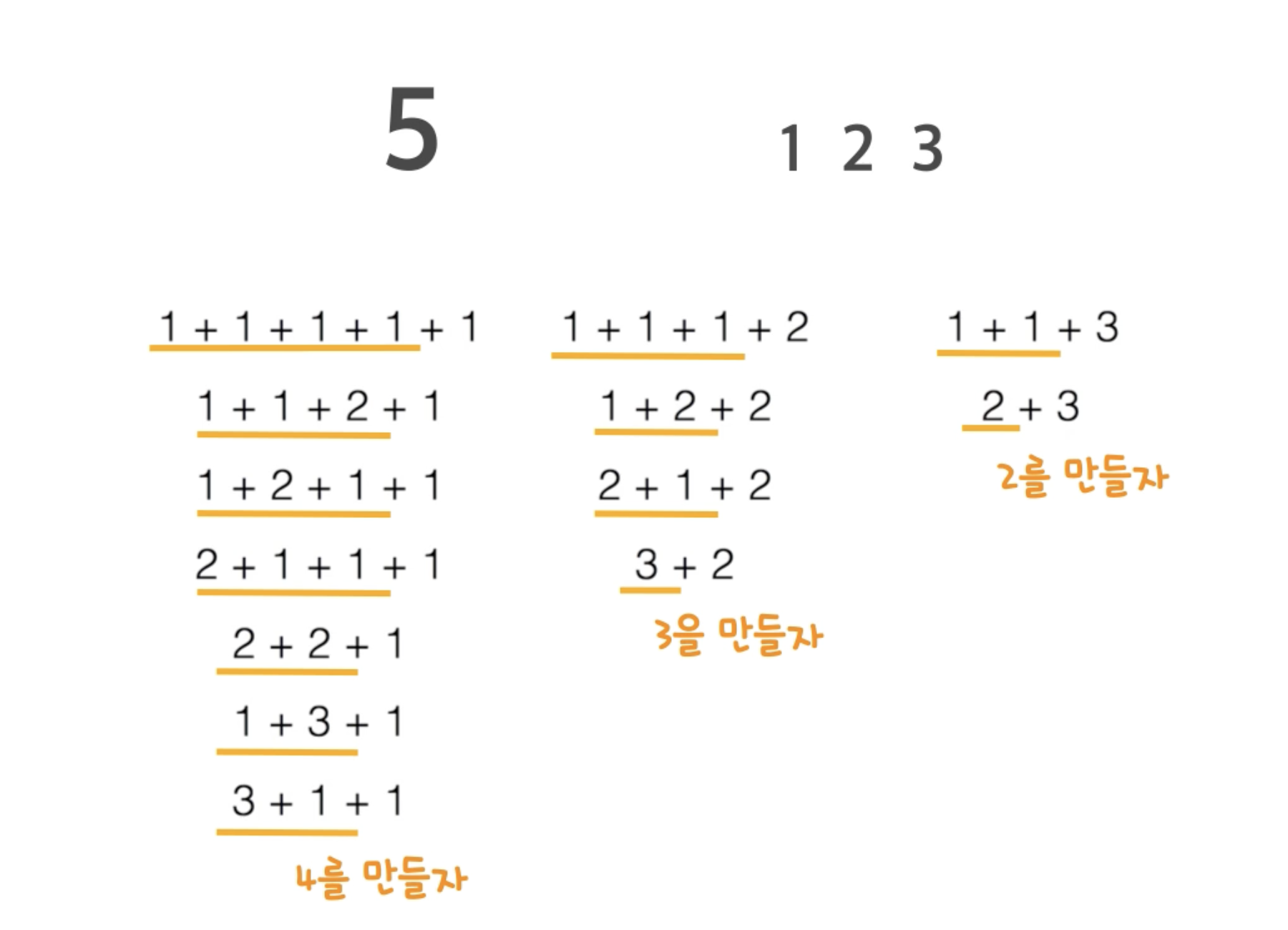
2. 점화식 구하기 -> T(i) = T(i-1) + T(i-2) + T(i-3)....+ T(i-m)
3. 문제를 해결하기
어떻게 저런 식이 나왔는가?
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] numbers = new int[100001];
numbers[1] = 1;
numbers[2] = 2;
numbers[3] = 4;
for (int i = 4; i<numbers.length; i++){
numbers[i] = (numbers[i-1] + numbers[i-2] +numbers[i-3])%1000007;
}
System.out.println(numbers[n]);
}
}여기선 문제에서 숫자 1,2,3을 사용한다고 하였으니 m의 값은 3이 된다.
제곱수의 합
문제풀이의 순서에 맞게 풀어보자
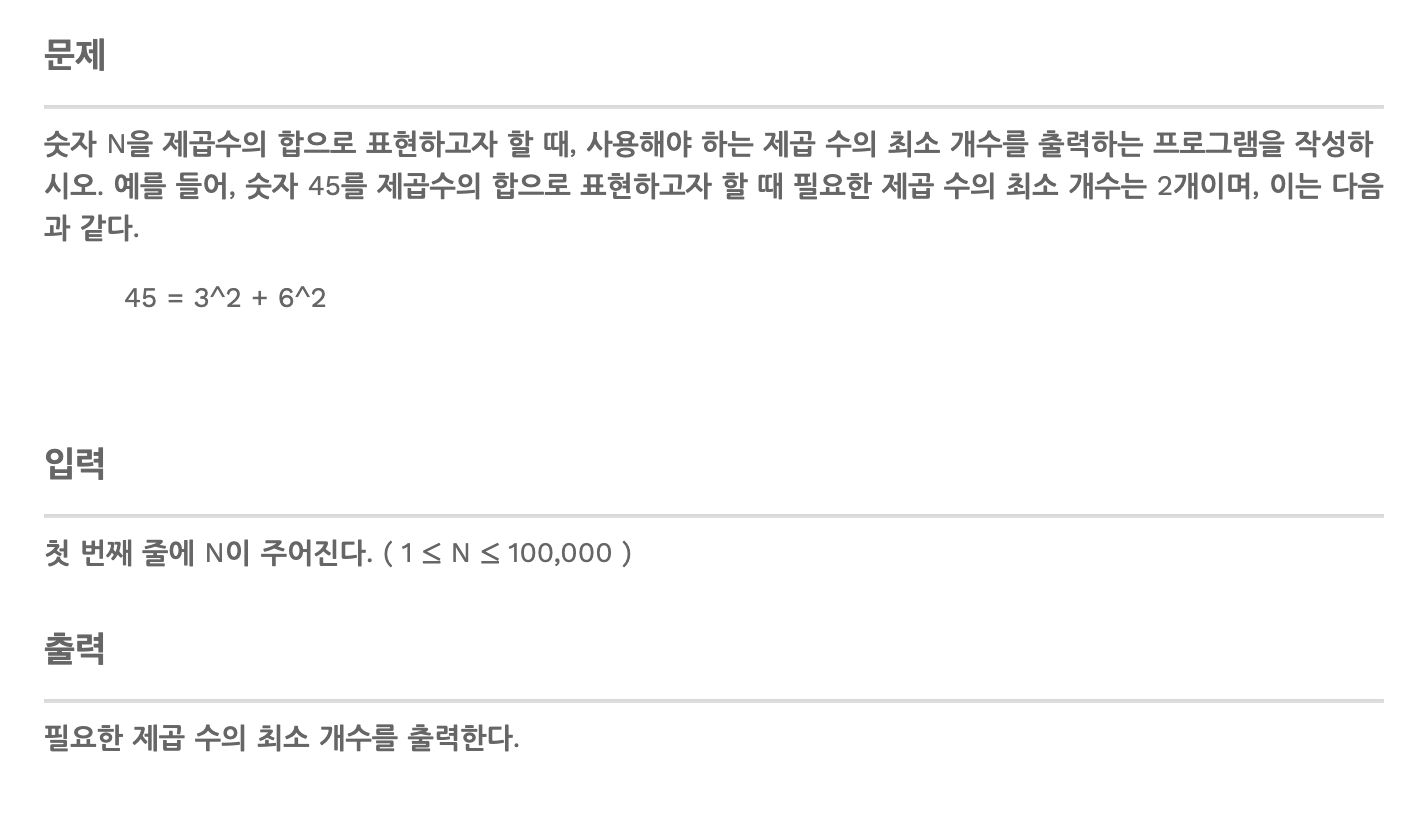
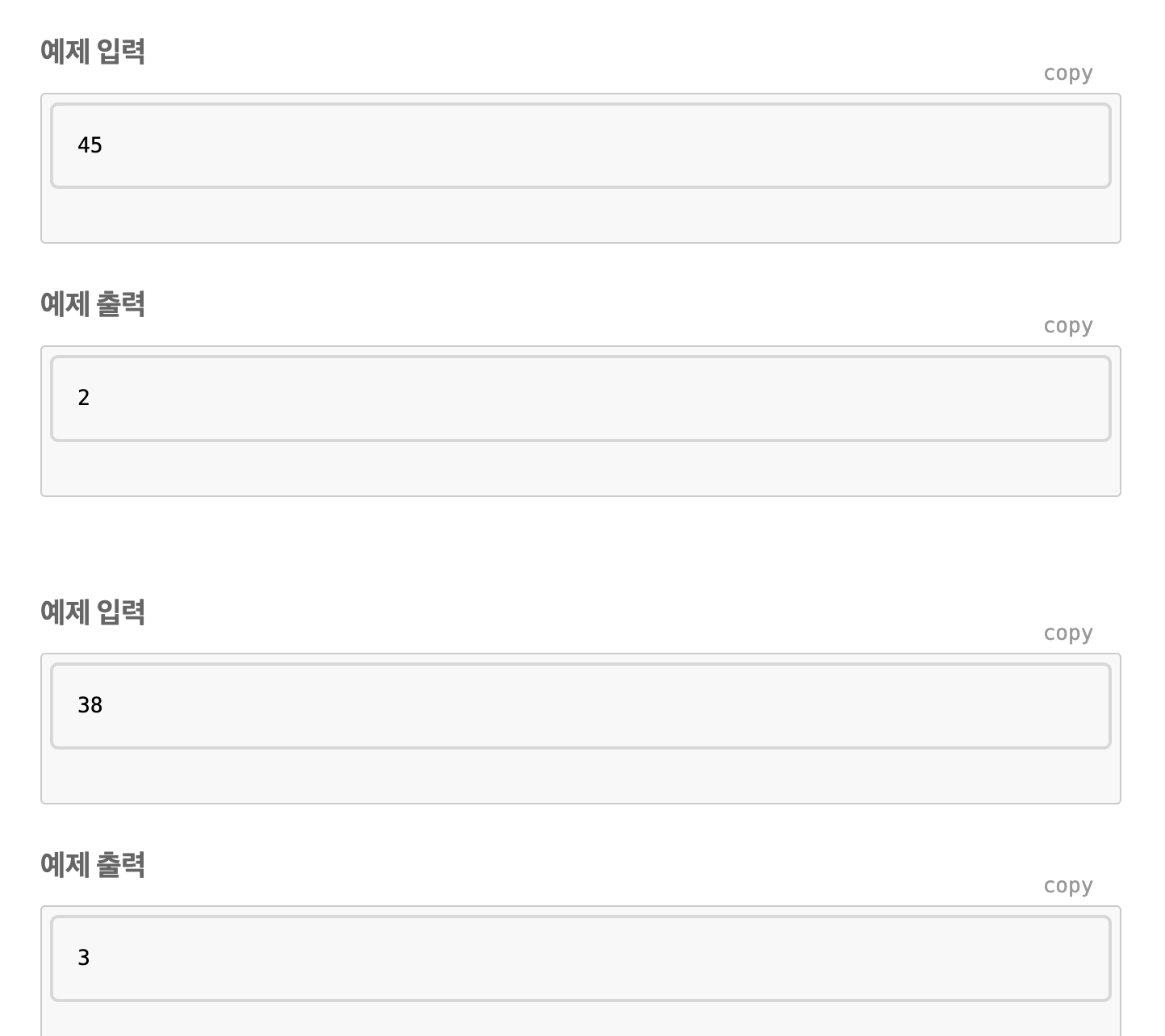
1. 부분 문제를 정의한다. -> T(i) = 숫자 i를 제곱수로 나타낼 때 사용해야 하는 최소 제곱수의 개수
2. 점화식 구하기 -> T(i) = Min(T(j) + 1), j = i -?^2
3. 문제를 해결하기
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] numbers = new int[n+1];
for (int i = 1; i<=n;i++){
numbers[i] = Integer.MAX_VALUE;
for (int j = 1;;j++){
if (i - (j*j) <0)break;
else if (i == j*j)numbers[i] = 1;
else {
numbers[i] = Math.min(numbers[i - j*j] + 1,numbers[i]);
}
}
}
System.out.println(numbers[n]);
}
}위의 식이 이해가 가지 않는다면 아래의 그림을 보면 이해가 될 것이다.
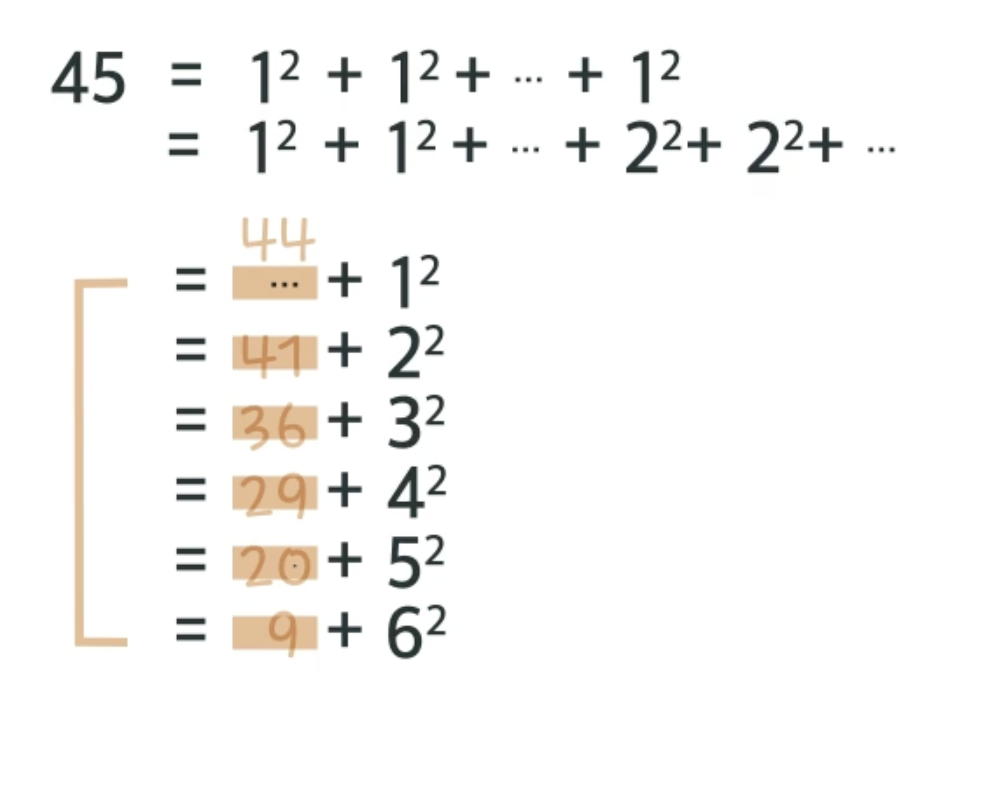
위의 그림을 식으로 생각해보면
T(44) + 1;
T(41) + 1;
T(36) + 1;
T(29) + 1;
T(20) + 1;
T(9) + 1;
이 된다.
버튼 누르기

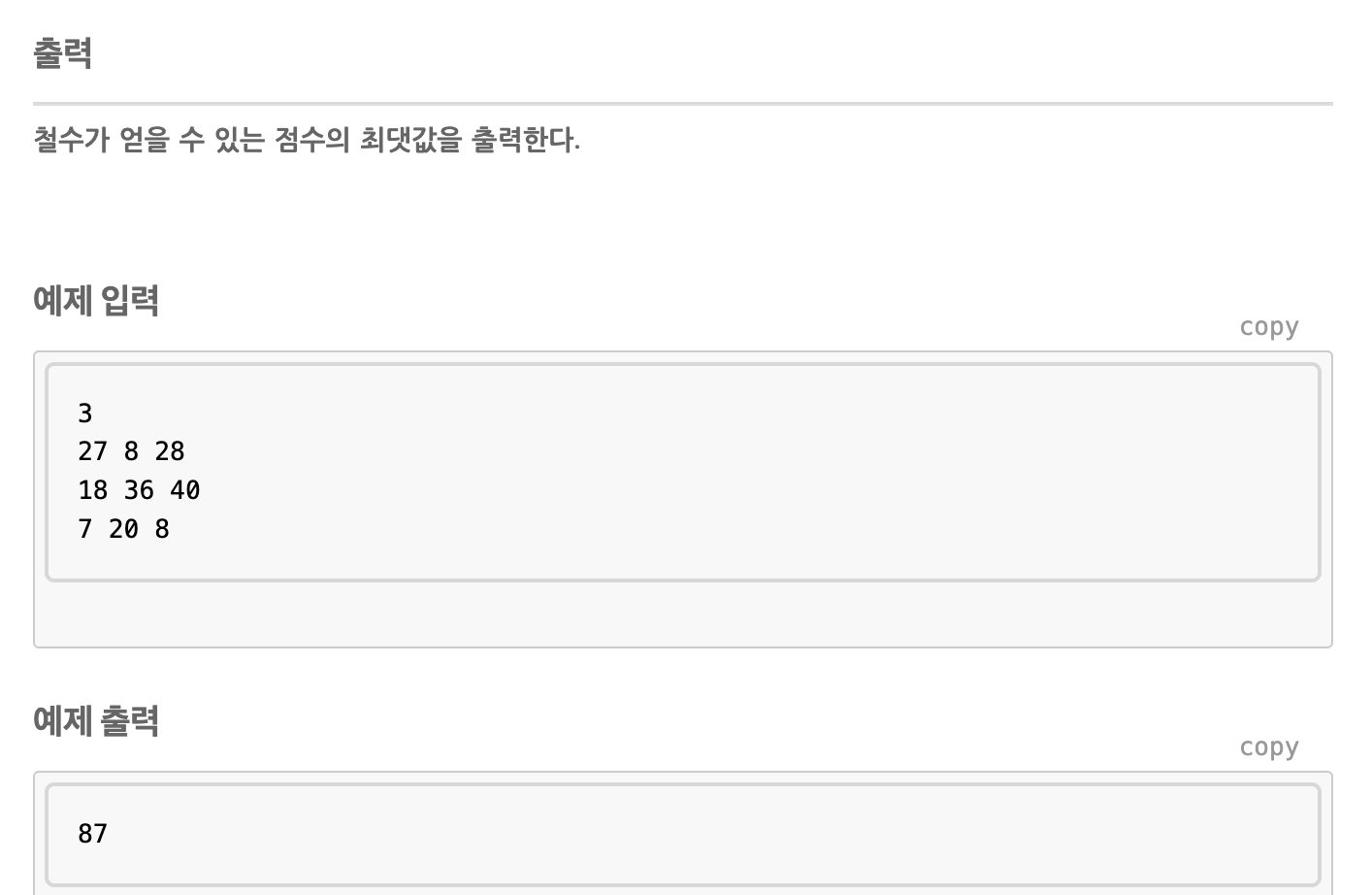
개인적으로 쉽지 않은 문제였다. DP가 낯설기도 했고,
부분 문제를 어떻게 정의할지 조차 생각하지 못하여 시간이 오래 걸린 문제이다.
/**
* 3
* 27 8 28
* 18 36 40
* 7 20 8
*
* 인덱스가 0 일때 이전값에서 1~2중 큰값을 선택
* 인덱스가 1 일때 이전값에서 0,2중 큰값을 선택
* 인덱스가 2일때 이전값에서 0,1중 큰값을 선택
* T[n] = data[n] + T[n-1]
*
*/
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[][] data = new int[n][3];
int[] one = new int[n];
int[] two = new int[n];
int[] three = new int[n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < 3; j++) {
data[i][j] = sc.nextInt();
}
}
one[0] = data[0][0];
two[0] = data[0][1];
three[0] = data[0][2];
one[1] = data[1][0] + Math.max(two[0], three[0]);
two[1] = data[1][1] + Math.max(one[0], three[0]);
three[1] = data[1][2] + Math.max(two[0], one[0]);
for (int i = 2; i < n; i++) {
one[i] = data[i][0] + Math.max(two[i-1],three[i-1]);
two[i] = data[i][1] + Math.max(one[i-1],three[i-1]);
three[i] = data[i][2] + Math.max(two[i-1],one[i-1]);
}
System.out.println(Math.max(one[n-1],Math.max(two[n-1],three[n-1])));
}
}이 문제를 풀고 나서 DP에 대한 이해도가 많이 높아졌다고 생각한다.
모든 버튼들이 이전 버튼에 영향을 받기 때문에 배열을 각각 만들어 주는 것이 중요 포인트라고 생각한다.
또한 잘 동작한다고 가정하고 점화식을 세우는 것이 중요한 것 같다.
카드놀이

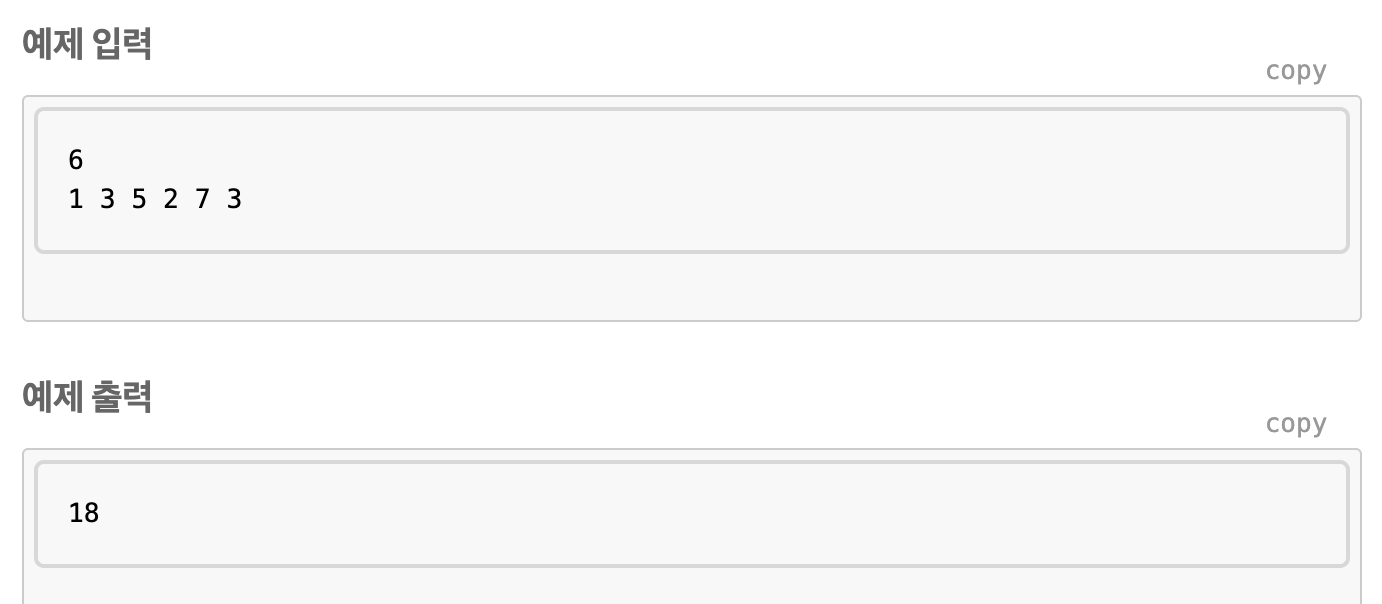
이 문제는 어떻게 나타낼 수 있을까?
우선 T(i)는 0~i까지의 카드가 있고, 그때 얻을 수 있는 최댓값이다.
이 문제의 경우 2가지 상황이 있다.

이를 이용하여 풀어보자.
import java.util.Scanner;
/**
* 1 3 5 2 7 3 마지막을 기준으로보자. 3을 마지막에 선택하냐 안하냐
* 1.선택안함 -> T[n-1]
* 2.선택함 - 7 3 의 경우 data[n] + data[n-1] + T[n-2] - 2 3 의 경우
* data[n-2] + data[n] + T[n-3]
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] data = new int[n];
int[] T = new int[n];
for (int i = 0; i < data.length; i++) {
data[i] = sc.nextInt();
}
T[0] = data[0];
T[1] = data[0] + data[1];
T[2] = Math.max(data[0] + data[1], Math.max(data[1] + data[2], data[0] + data[2]));
for (int i = 3; i < n; i++) {
T[i] = Math.max(T[i - 1], Math.max(data[i] + data[i - 1] + T[i - 3]
, data[i] + T[i - 2]));
}
System.out.println(T[n - 1]);
}
}
자원 채취
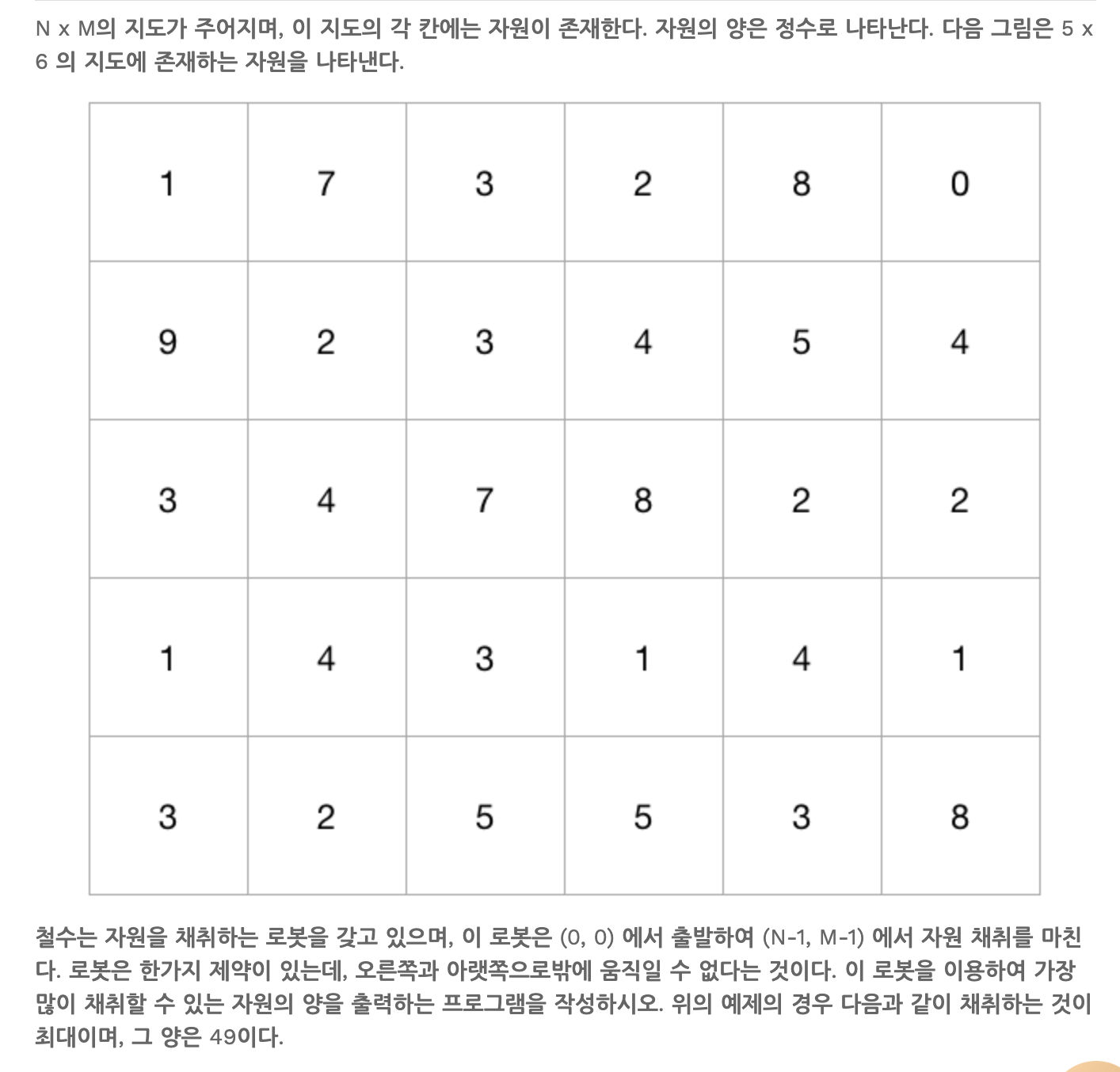
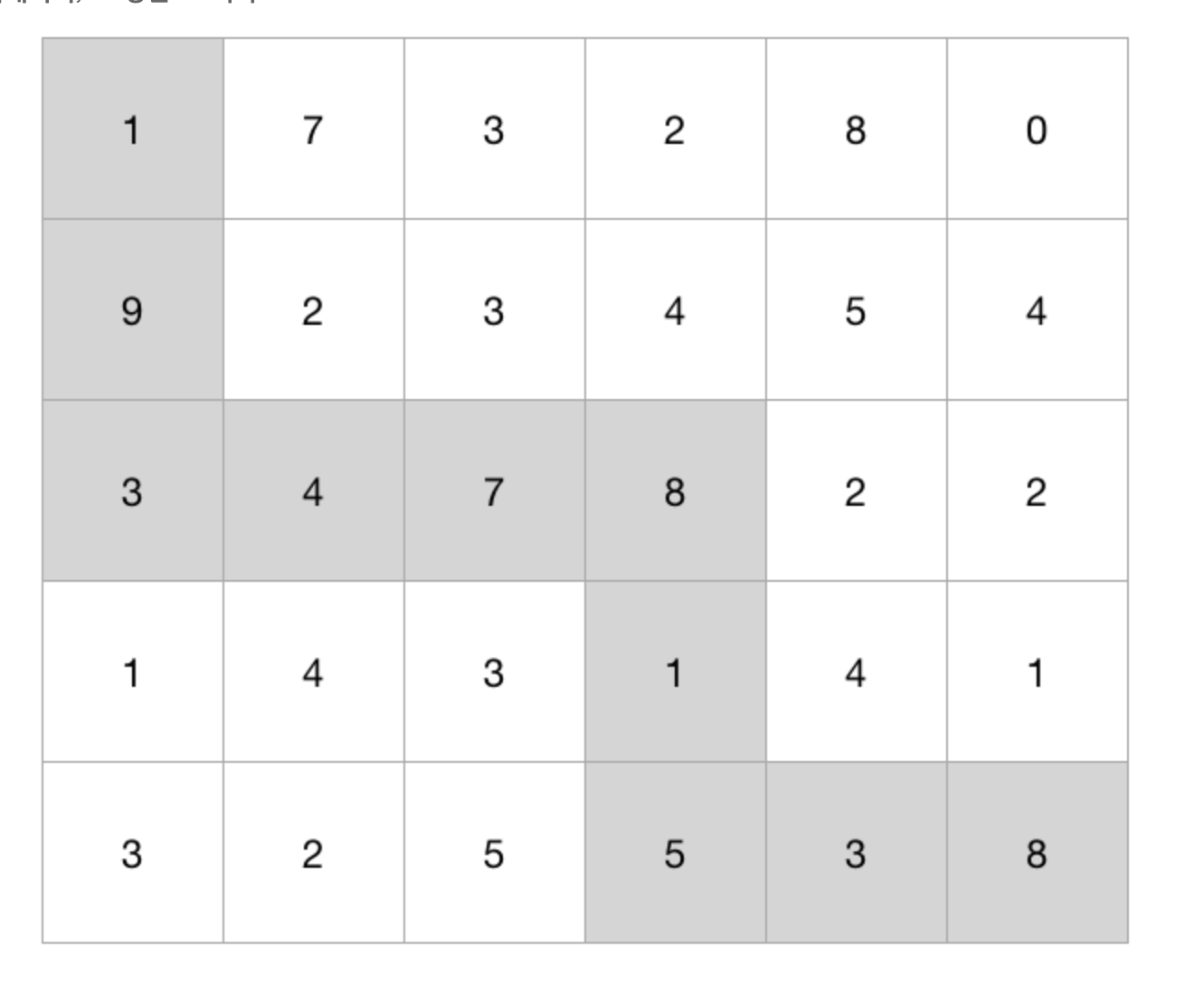
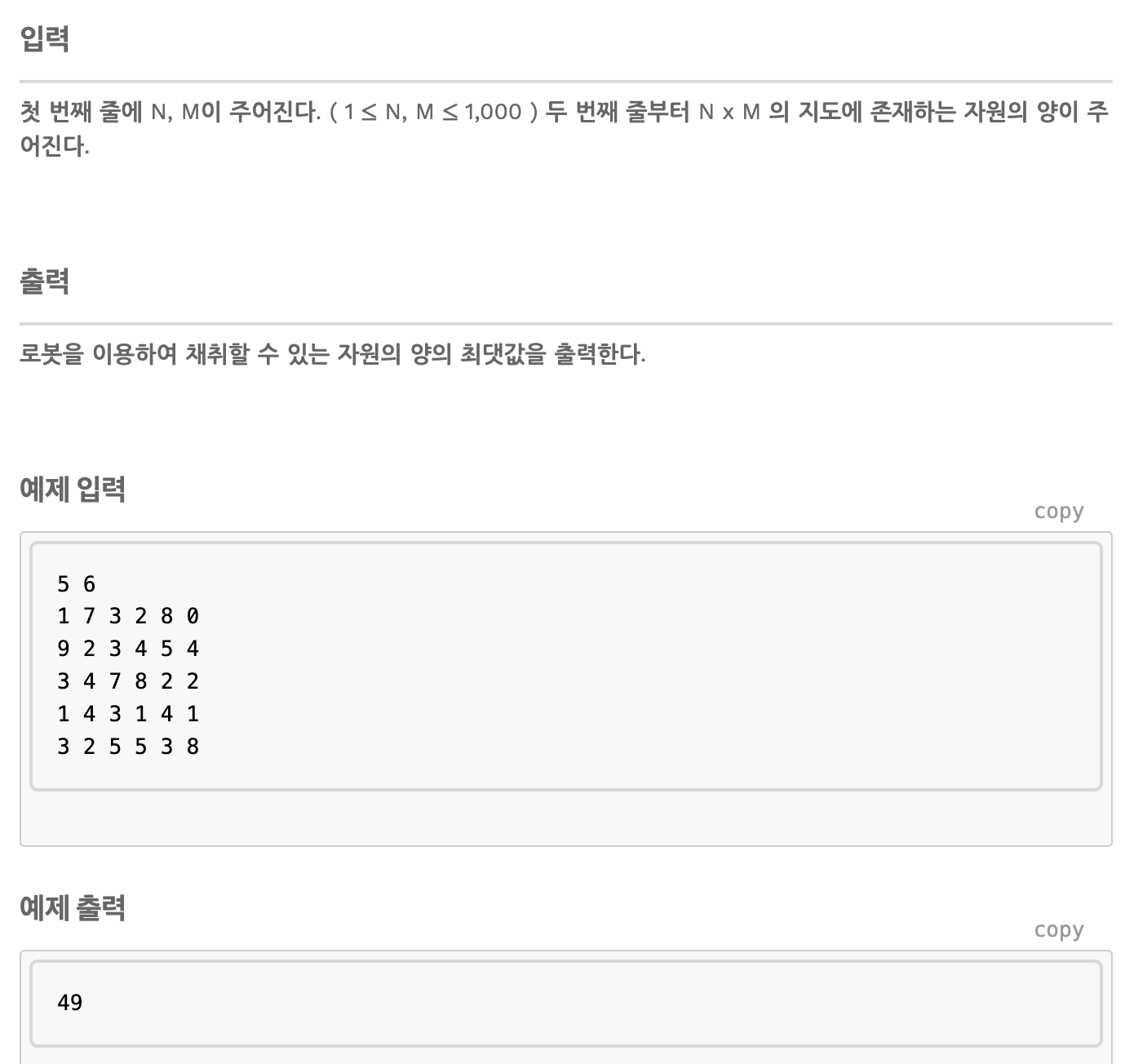
처음에 이 문제는 당연하게 DFS로 푸는 문제인 줄 알고, DFS를 적용해보았는데 바로 런타임 에러가 떠버렸다.
이 문제를 DP를 활용하여 어떻게 풀 수 있을까?
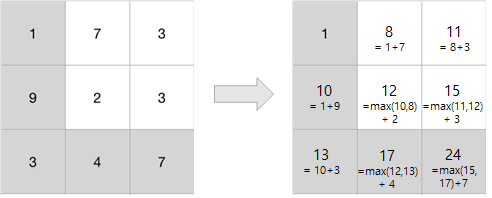
map [i][j]라고 하고 여기에 값을 집어넣는다면,
i ==0일 때 위에서 올 수 있는 경로가 없기 때문에 오른쪽으로 가는 방향만 확인하면 된다.
j == 0일 때 오른쪽에서 올 수 있는 경로가 없기 때문에 아래로 가는 방향만 확인하면 된다.
즉 T [i] = Math.max(T [i-1][j], T [i][j-1]) + data; 가 된다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int[][] T = new int[n][m];
for (int i = 0; i < n; i++) {
int sum =0;
for (int j = 0; j < m; j++) {
int value = sc.nextInt();
if (i == 0){
sum+=value;
T[i][j] = sum;
} else if (j == 0) {
T[i][j] = T[i-1][j] +value;
}else {
T[i][j] = Math.max(T[i-1][j],T[i][j-1])+value;
}
}
}
System.out.println(T[n-1][m-1]);
}
}이 문제에서 핵심은 처음부터 입력을 다 받는 것이 아닌, 받는 즉시 T의 값을 채우는 것이다.
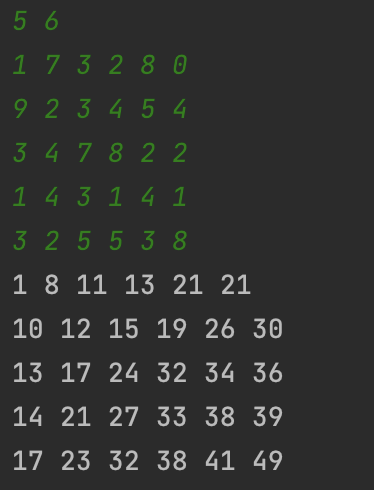
실제 T의 값들이 넣어진 상태이다. 숫자를 보면 각각의 자리에 최댓값이 저장되어 있는 것을 알 수 있다.
두 문자열 사이의 거리

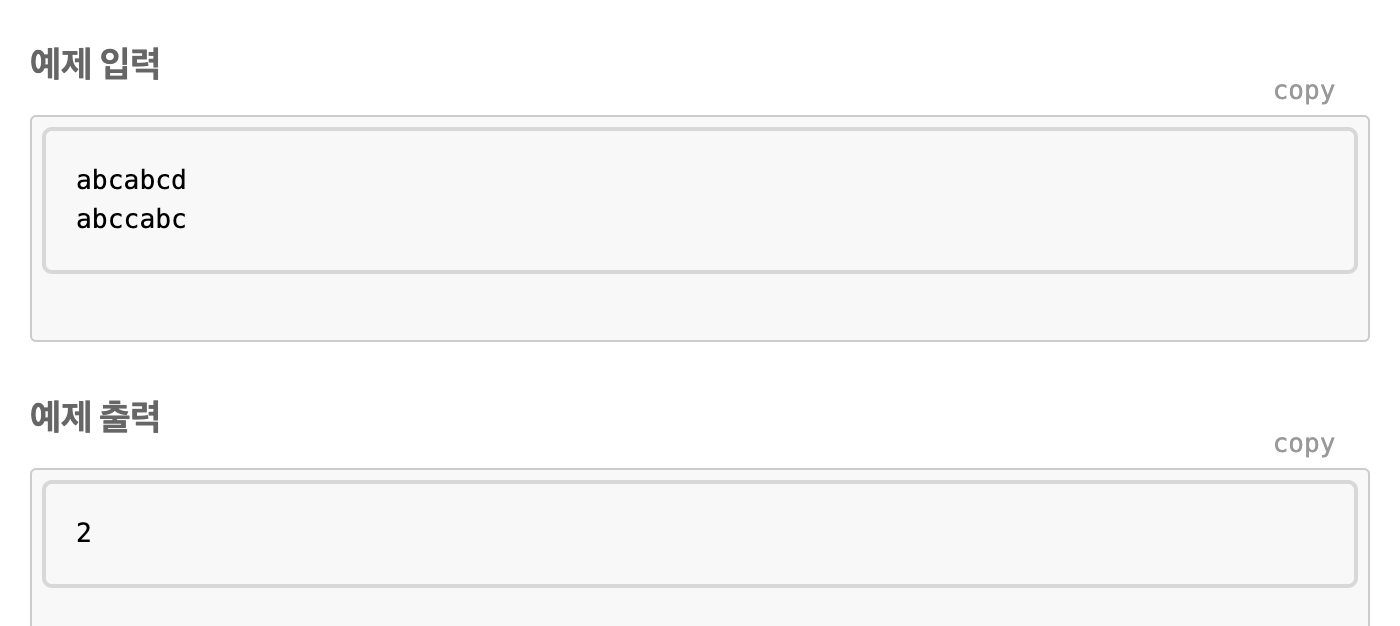
이 문제를 어떻게 풀지 감이 전혀 잡히지 않았다.
그러다 "편집 거리 알고리즘"을 사용한다는 것을 알게 되었고 이를 활용하여 풀 수 있었다.
편집 거리 알고리즘은 두 문자열의 유사도를 판단하는 알고리즘이다.
수정, 삽입, 삭제 기능이 있다고 할 때 몇 번의 동작이 필요한지 측정한다. 문자열 내에서 위치 변환 같은 기능이 없다.
2차원 메모 이제이 션 배열을 사용하는 Dynamic Programming의 한 종류이다.
편집 거리 알고리즘의 규칙
- str1에서 i번째 문자와 str2에서 j번째 문자를 서로 비교한다.
- 두 문자가 같으면 dp [i-1][j-1]의 값을 그대로 가져온다.
- 두 문자가 다르면 dp [i-1][j], dp [i][j-1], dp [i-1][j-1] 중 최솟값에 1을 더해서 dp [i][j]에 저장
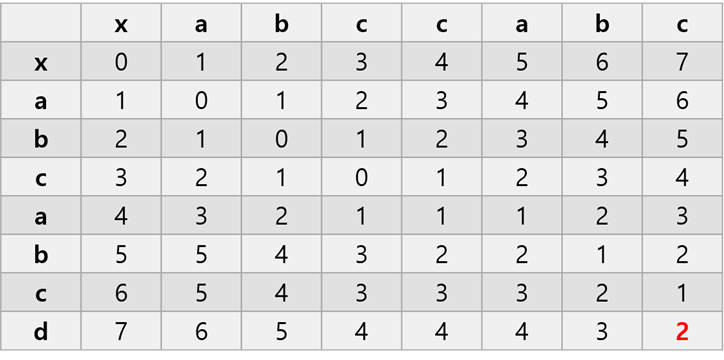
이를 활용하면 아래와 같은 표를 만들 수 있다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String a = sc.nextLine();
String b = sc.nextLine();
int aSize = a.length();
int bSize = b.length();
int[][] map = new int[aSize + 1][bSize + 1];
for (int i = 0; i<= aSize; i++){
map[i][0] = i;
}
for (int i = 0; i<= aSize; i++){
map[0][i] = i;
}
for (int i = 1; i <= aSize; i++) {
for (int j = 1; j<=bSize; j++){
if (a.charAt(i-1)==b.charAt(j-1))map[i][j] = map[i-1][j-1];
else map[i][j] = Math.min(map[i-1][j-1], Math.min(map[i-1][j], map[i][j-1]))+1;
}
}
System.out.println(map[aSize][bSize]);
}
}편집 거리 알고리즘의 규칙이 점화식 자체가 된다.

실제 저장된 값이 편집 거리 알고리즘을 이용한 값과 동일하다.
배운 점
위의 문제들을 전부 푸는데 생각보다 많은 시간이 걸렸다.
DP를 처음 접하기 때문에 생각보다 이해하고 적용하는데 시간이 많이 걸린 것 같다.
DP를 사용하여 푸는 문제를 다른 방법을 사용하여 풀 수 있는 경우도 있지만(DFS),
시간 복잡도의 측면에서 DP를 사용하면 너무나 빠르기 때문에 DP를 사용할 수 있다면 당연하게 DP를 사용해야겠다.
부분 문제를 정의하는 것이 가장 어렵고 난해하다는 생각을 하였다. 문제를 많이 풀어보고 계속해서 연습해야겠다.
알고리즘은 많이 풀어볼수록 실력이 빨리 성장한다고 느꼈다.
DP문제들을 다시 풀어보며 정리해야겠다.
'PS > 알고리즘' 카테고리의 다른 글
| 최소 신장 트리(Minimum Spanning Tree, MST) (0) | 2023.05.24 |
|---|---|
| 비트마스크(BitMask) (2) | 2023.01.20 |
| 다익스트라 (0) | 2022.12.18 |
| 너비 우선 탐색(BFS) (1) | 2022.11.14 |
| 깊이 우선 탐색(DFS) (2) | 2022.11.06 |
동적 계획법(Dynamic Proframming)이란?
부분 문제를 해결한 결과를 이용하여 전체 문제를 해결하는 것
작은 나를 해결함으로써 더 큰 나를 해결함
동적 계획법의 문제 풀이 순서
1. 부분 문제를 정의한다.
- 무슨 값을 구할지를 정의한다.
2. 점화식을 구한다.
- 그 값을 어떻게 구할지에 대한 식을 세운다.
( 부분은 풀려있다고 가정)
3. 문제를 해결한다.
- 값을 직접 구하는 코드를 작성한다.
동적 계획법을 활용한 대표적인 예시
피보나치 수 구하기가 있다.

점화식을 활용하기 위해 index 0,1에 해당하는 값을 미리 채워주어야 한다.
반복문을 통해 이전의 값을 활용하여 채워주면서 나아가면 된다.
동적 계획법 활용 문제
개인적으로 동적 계획법 자체는 쉽지만 부분 문제를 정의하는 것이 어렵다고 생각한다.
많은 문제를 풀며 익히는 것이 중요한 것 같다.
직사각형 배치의 경우의 수


문제풀이의 순서에 맞게 풀어보자
1. 부분 문제를 정의한다. -> T(i) = 2* i의 상자를 채우는 경우의 수
2. 점화식 구하기 -> T(i) = T(i-1) + T(i-2) == 피보나치수열
3. 문제를 해결하기
어떻게 저런 식이 나왔는가?


누적 합을 이용하는 문제이다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] rectangle = new int[n+1];
rectangle[1] = 1;
rectangle[2] = 2;
for (int i = 3; i < rectangle.length; i++) {
rectangle[i] = (rectangle[i - 1] + rectangle[i - 2])%1000007;
}
System.out.println(rectangle[n]);
}
}
숫자 만들기


문제풀이의 순서에 맞게 풀어보자
1. 부분 문제를 정의한다. -> T(i) = 1 ~ M의 수를 이용하여 i를 만드는 경우의 수
2. 점화식 구하기 -> T(i) = T(i-1) + T(i-2) + T(i-3)....+ T(i-m)
3. 문제를 해결하기
어떻게 저런 식이 나왔는가?

import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] numbers = new int[100001];
numbers[1] = 1;
numbers[2] = 2;
numbers[3] = 4;
for (int i = 4; i<numbers.length; i++){
numbers[i] = (numbers[i-1] + numbers[i-2] +numbers[i-3])%1000007;
}
System.out.println(numbers[n]);
}
}여기선 문제에서 숫자 1,2,3을 사용한다고 하였으니 m의 값은 3이 된다.
제곱수의 합


문제풀이의 순서에 맞게 풀어보자
1. 부분 문제를 정의한다. -> T(i) = 숫자 i를 제곱수로 나타낼 때 사용해야 하는 최소 제곱수의 개수
2. 점화식 구하기 -> T(i) = Min(T(j) + 1), j = i -?^2
3. 문제를 해결하기
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] numbers = new int[n+1];
for (int i = 1; i<=n;i++){
numbers[i] = Integer.MAX_VALUE;
for (int j = 1;;j++){
if (i - (j*j) <0)break;
else if (i == j*j)numbers[i] = 1;
else {
numbers[i] = Math.min(numbers[i - j*j] + 1,numbers[i]);
}
}
}
System.out.println(numbers[n]);
}
}위의 식이 이해가 가지 않는다면 아래의 그림을 보면 이해가 될 것이다.
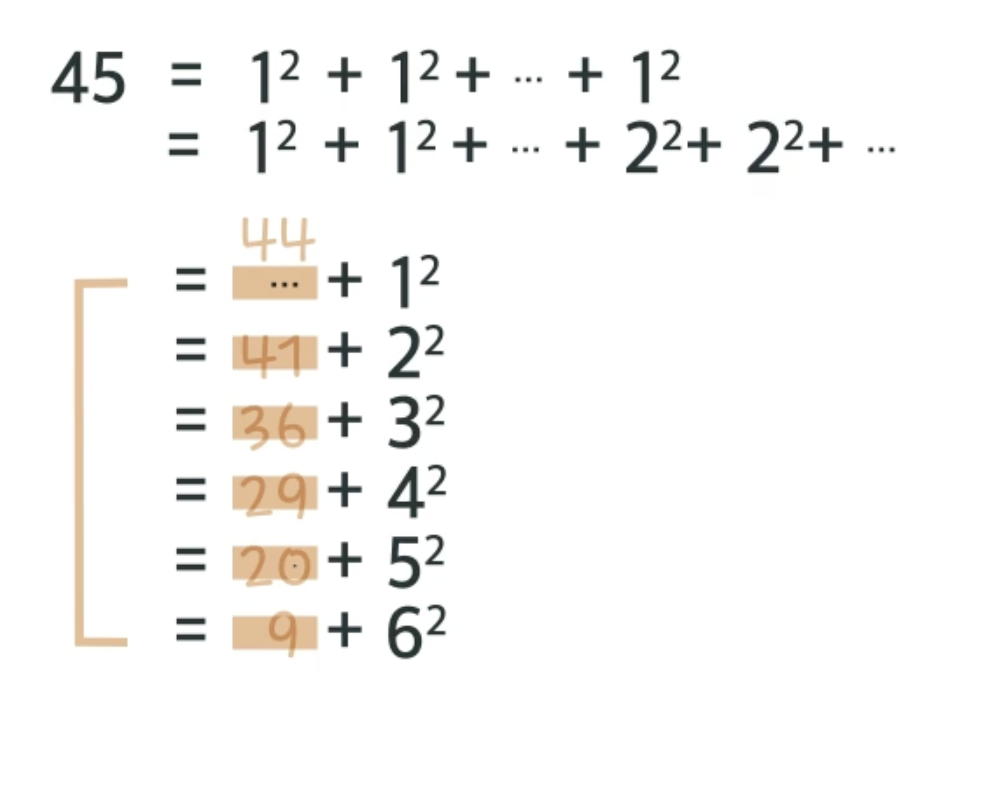
위의 그림을 식으로 생각해보면
T(44) + 1;
T(41) + 1;
T(36) + 1;
T(29) + 1;
T(20) + 1;
T(9) + 1;
이 된다.
버튼 누르기


개인적으로 쉽지 않은 문제였다. DP가 낯설기도 했고,
부분 문제를 어떻게 정의할지 조차 생각하지 못하여 시간이 오래 걸린 문제이다.
/**
* 3
* 27 8 28
* 18 36 40
* 7 20 8
*
* 인덱스가 0 일때 이전값에서 1~2중 큰값을 선택
* 인덱스가 1 일때 이전값에서 0,2중 큰값을 선택
* 인덱스가 2일때 이전값에서 0,1중 큰값을 선택
* T[n] = data[n] + T[n-1]
*
*/
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[][] data = new int[n][3];
int[] one = new int[n];
int[] two = new int[n];
int[] three = new int[n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < 3; j++) {
data[i][j] = sc.nextInt();
}
}
one[0] = data[0][0];
two[0] = data[0][1];
three[0] = data[0][2];
one[1] = data[1][0] + Math.max(two[0], three[0]);
two[1] = data[1][1] + Math.max(one[0], three[0]);
three[1] = data[1][2] + Math.max(two[0], one[0]);
for (int i = 2; i < n; i++) {
one[i] = data[i][0] + Math.max(two[i-1],three[i-1]);
two[i] = data[i][1] + Math.max(one[i-1],three[i-1]);
three[i] = data[i][2] + Math.max(two[i-1],one[i-1]);
}
System.out.println(Math.max(one[n-1],Math.max(two[n-1],three[n-1])));
}
}이 문제를 풀고 나서 DP에 대한 이해도가 많이 높아졌다고 생각한다.
모든 버튼들이 이전 버튼에 영향을 받기 때문에 배열을 각각 만들어 주는 것이 중요 포인트라고 생각한다.
또한 잘 동작한다고 가정하고 점화식을 세우는 것이 중요한 것 같다.
카드놀이


이 문제는 어떻게 나타낼 수 있을까?
우선 T(i)는 0~i까지의 카드가 있고, 그때 얻을 수 있는 최댓값이다.
이 문제의 경우 2가지 상황이 있다.

이를 이용하여 풀어보자.
import java.util.Scanner;
/**
* 1 3 5 2 7 3 마지막을 기준으로보자. 3을 마지막에 선택하냐 안하냐
* 1.선택안함 -> T[n-1]
* 2.선택함 - 7 3 의 경우 data[n] + data[n-1] + T[n-2] - 2 3 의 경우
* data[n-2] + data[n] + T[n-3]
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] data = new int[n];
int[] T = new int[n];
for (int i = 0; i < data.length; i++) {
data[i] = sc.nextInt();
}
T[0] = data[0];
T[1] = data[0] + data[1];
T[2] = Math.max(data[0] + data[1], Math.max(data[1] + data[2], data[0] + data[2]));
for (int i = 3; i < n; i++) {
T[i] = Math.max(T[i - 1], Math.max(data[i] + data[i - 1] + T[i - 3]
, data[i] + T[i - 2]));
}
System.out.println(T[n - 1]);
}
}
자원 채취



처음에 이 문제는 당연하게 DFS로 푸는 문제인 줄 알고, DFS를 적용해보았는데 바로 런타임 에러가 떠버렸다.
이 문제를 DP를 활용하여 어떻게 풀 수 있을까?

map [i][j]라고 하고 여기에 값을 집어넣는다면,
i ==0일 때 위에서 올 수 있는 경로가 없기 때문에 오른쪽으로 가는 방향만 확인하면 된다.
j == 0일 때 오른쪽에서 올 수 있는 경로가 없기 때문에 아래로 가는 방향만 확인하면 된다.
즉 T [i] = Math.max(T [i-1][j], T [i][j-1]) + data; 가 된다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int[][] T = new int[n][m];
for (int i = 0; i < n; i++) {
int sum =0;
for (int j = 0; j < m; j++) {
int value = sc.nextInt();
if (i == 0){
sum+=value;
T[i][j] = sum;
} else if (j == 0) {
T[i][j] = T[i-1][j] +value;
}else {
T[i][j] = Math.max(T[i-1][j],T[i][j-1])+value;
}
}
}
System.out.println(T[n-1][m-1]);
}
}이 문제에서 핵심은 처음부터 입력을 다 받는 것이 아닌, 받는 즉시 T의 값을 채우는 것이다.

실제 T의 값들이 넣어진 상태이다. 숫자를 보면 각각의 자리에 최댓값이 저장되어 있는 것을 알 수 있다.
두 문자열 사이의 거리


이 문제를 어떻게 풀지 감이 전혀 잡히지 않았다.
그러다 "편집 거리 알고리즘"을 사용한다는 것을 알게 되었고 이를 활용하여 풀 수 있었다.
편집 거리 알고리즘은 두 문자열의 유사도를 판단하는 알고리즘이다.
수정, 삽입, 삭제 기능이 있다고 할 때 몇 번의 동작이 필요한지 측정한다. 문자열 내에서 위치 변환 같은 기능이 없다.
2차원 메모 이제이 션 배열을 사용하는 Dynamic Programming의 한 종류이다.
편집 거리 알고리즘의 규칙
- str1에서 i번째 문자와 str2에서 j번째 문자를 서로 비교한다.
- 두 문자가 같으면 dp [i-1][j-1]의 값을 그대로 가져온다.
- 두 문자가 다르면 dp [i-1][j], dp [i][j-1], dp [i-1][j-1] 중 최솟값에 1을 더해서 dp [i][j]에 저장
이를 활용하면 아래와 같은 표를 만들 수 있다.

import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String a = sc.nextLine();
String b = sc.nextLine();
int aSize = a.length();
int bSize = b.length();
int[][] map = new int[aSize + 1][bSize + 1];
for (int i = 0; i<= aSize; i++){
map[i][0] = i;
}
for (int i = 0; i<= aSize; i++){
map[0][i] = i;
}
for (int i = 1; i <= aSize; i++) {
for (int j = 1; j<=bSize; j++){
if (a.charAt(i-1)==b.charAt(j-1))map[i][j] = map[i-1][j-1];
else map[i][j] = Math.min(map[i-1][j-1], Math.min(map[i-1][j], map[i][j-1]))+1;
}
}
System.out.println(map[aSize][bSize]);
}
}편집 거리 알고리즘의 규칙이 점화식 자체가 된다.

실제 저장된 값이 편집 거리 알고리즘을 이용한 값과 동일하다.
배운 점
위의 문제들을 전부 푸는데 생각보다 많은 시간이 걸렸다.
DP를 처음 접하기 때문에 생각보다 이해하고 적용하는데 시간이 많이 걸린 것 같다.
DP를 사용하여 푸는 문제를 다른 방법을 사용하여 풀 수 있는 경우도 있지만(DFS),
시간 복잡도의 측면에서 DP를 사용하면 너무나 빠르기 때문에 DP를 사용할 수 있다면 당연하게 DP를 사용해야겠다.
부분 문제를 정의하는 것이 가장 어렵고 난해하다는 생각을 하였다. 문제를 많이 풀어보고 계속해서 연습해야겠다.
알고리즘은 많이 풀어볼수록 실력이 빨리 성장한다고 느꼈다.
DP문제들을 다시 풀어보며 정리해야겠다.
'PS > 알고리즘' 카테고리의 다른 글
| 최소 신장 트리(Minimum Spanning Tree, MST) (0) | 2023.05.24 |
|---|---|
| 비트마스크(BitMask) (2) | 2023.01.20 |
| 다익스트라 (0) | 2022.12.18 |
| 너비 우선 탐색(BFS) (1) | 2022.11.14 |
| 깊이 우선 탐색(DFS) (2) | 2022.11.06 |
