비트마스크란?
- 비트마스크(BitMask)는 이진수를 사용하는 컴퓨터의 연산 방식을 이용하여,
정수의 이진수 표현을 자료 구조로 쓰는 기법을 말한다.
- 이진수는 0 또는 1을 이용하므로 하나의 비트(bit)가 표현할 수 있는 경우는 두 가지이다.
- 보통 어떤 비트가 1이면 "켜져 있다"라고 말하며, 0이면 "꺼져 있다"라고 말한다.
- 8 bits = 1byte
비트마스크를 사용하면 다음과 같은 이점을 얻을 수 있다.
- 수행시간이 빠르다.
- 코드가 짧다
- 메모리 사용량이 더 적다.
비트 연산자
AND연산 (&)
대응하는 두 비트가 모두 1일 때, 1을 반환
1010 & 1111 = 1010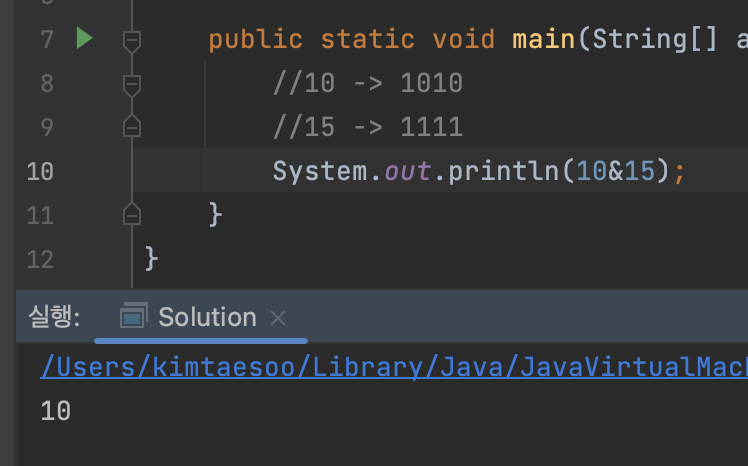
OR연산(|)
대응하는 두비트가 모두 1 또는 둘 중 하나라도 1이면, 1을 반환
1010 | 1111 = 1111
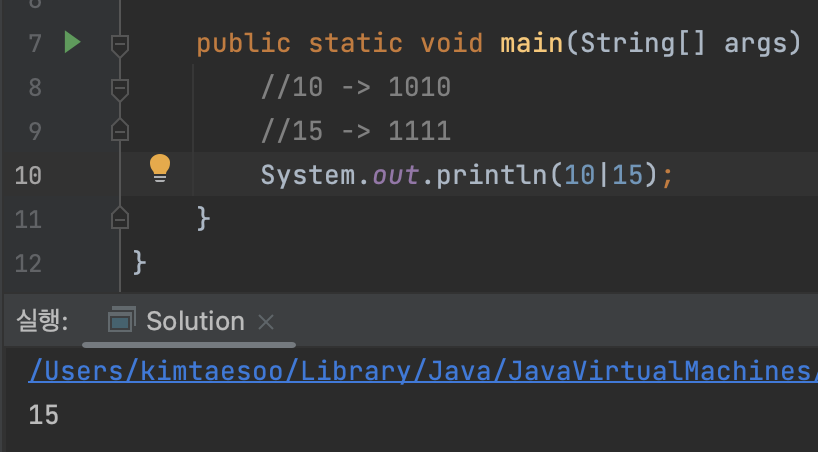
XOR연산(^)
대응하는 두 비트가 서로 다르면 1을 반환
1010 ^ 1111 = 0101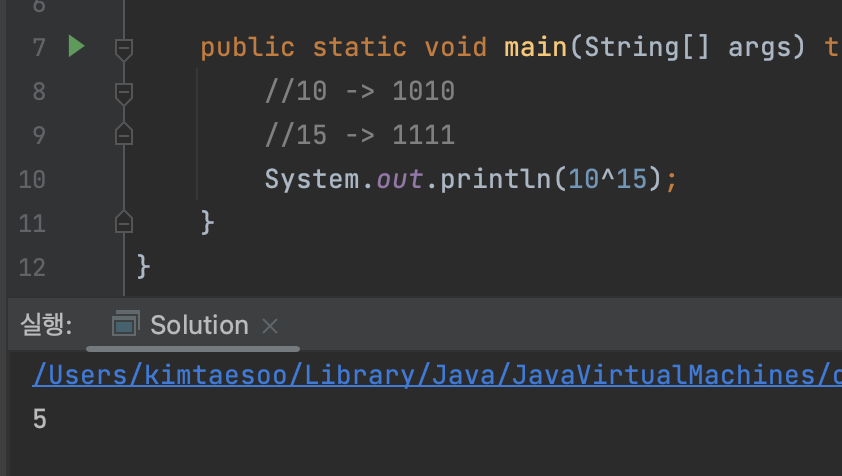
NOT연산(~)
비트의 값을 반전하여 반환
~1010=0101
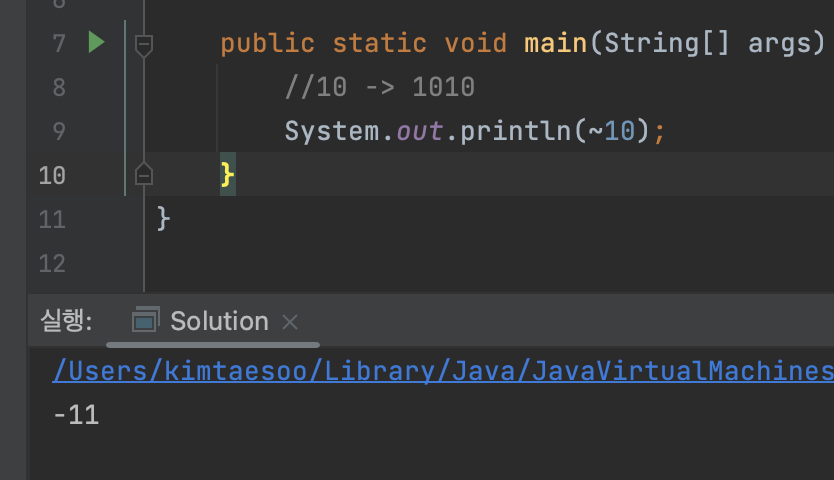
예상한 값인 5가 아닌 10에서 2의 보수를 취한 값이 나온다.
시프트연산(>>,<<)
왼쪽 또는 오른쪽으로 비트를 옮긴다.
00001010 << 2 = 101000
00001010 >> 2 = 000010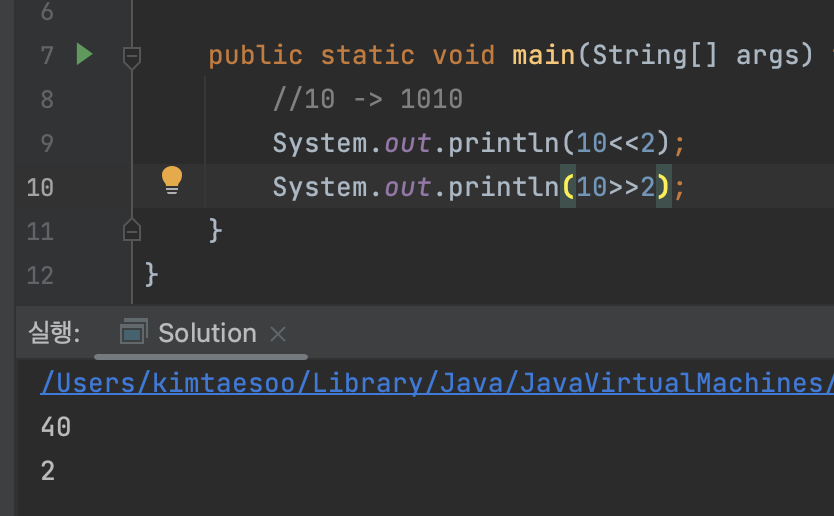
위의 연산들을 한눈에 비교해보자.
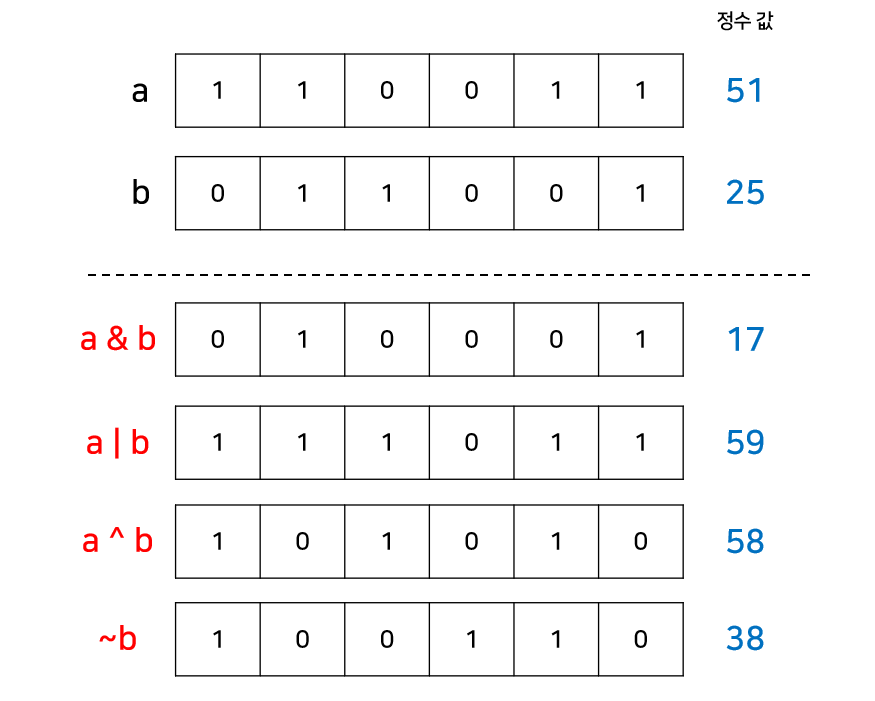
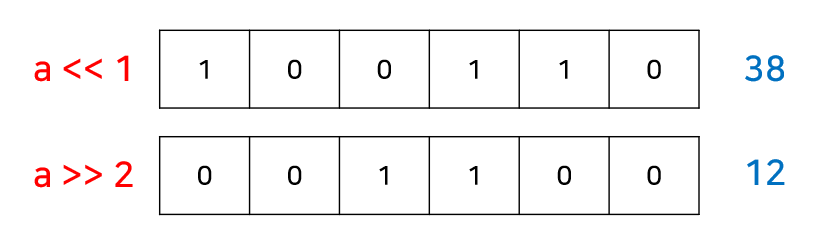
주의점
- 비트 연산자의 우선순위는 비교 연산자보다 낮다.
- ex) a = (10 & 6 == 2)라면 6==2 가먼저 계산되어 0(false)을 반환하고, 이후 10 & 0을 할당
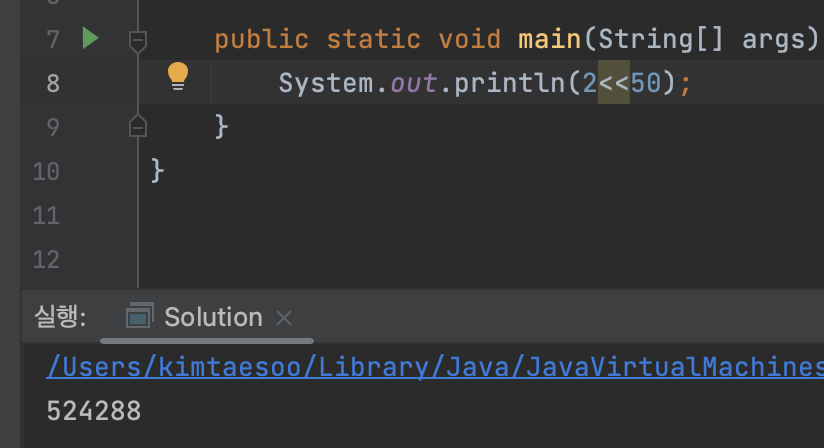
인텔리제이의 경우 에러가 난다.
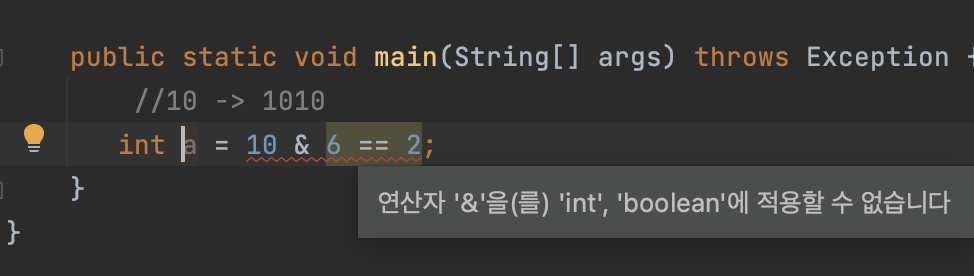
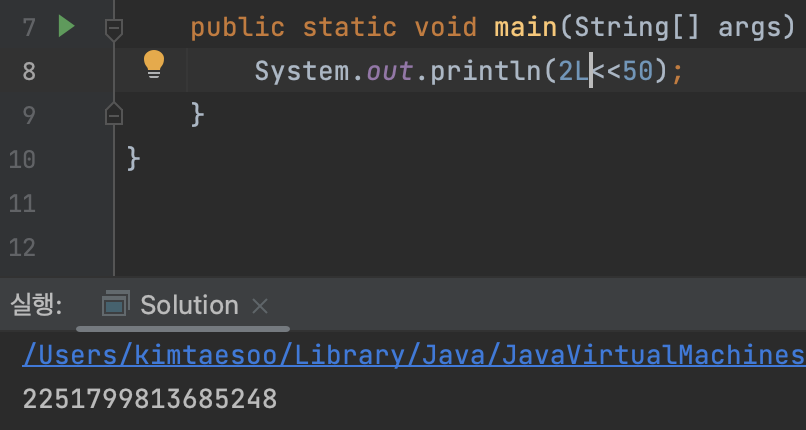
- 오버플로우(Overflow) 문제이다.
- 오버플로우를 잘 해결하려면 기본값의 타입을 잘 맞추어야 한다
비트마스크의 활용
비트 마스크를 어디에 활용할 수 있을까?
비트마스크는 집합 구현에 매우 효과적이다.
A를 집합이라 두고, 원소는 10개를 갖는다 가정하자.(0~9번째 원소)
쉽게 이해하는 방법은
{A, B, C, D}의 각 원소를 0001, 0010, 0100, 1000이라 생각하면 쉽게 이해될 것이다.
공집합, 모든 원소를 갖는 집합 구하기
공집합은 모든 원소가 없으므로 0을 공집합으로 표현가능하다.
반대로 모든 원소를 갖는 집합은 모든 bit가 1이어야 한다.
1111111111(2) -> (1<<10)-1과 동일하다.
원소 추가 (OR 연산)
A에 특정 원소를 추가하려면 해당하는 bit를 켜야 한다.(1)
A |= (1<<k) 이미 A에 원소에 포함되어 있다면 변화는 없다.
원소 삭제 (AND 연산)
A에 특정 원소를 삭제하려면 해당하는 bit를 꺼야 한다.(0)
A &=~(1<<k)를 사용하여 해당 원소를 0으로 만들 수 있다.
원소의 포함 여부 확인
if(A&(1<<k)) 특정 원소의 포함여부를 알려면, k번째 비트가 켜져 있는지 확인하면 된다.
원소의 토글 (XOR 연산)
A의 집합에서 해당원소가 없으면 추가하고, 있다면 삭제하려면
A^ =(1<<k)를 해주면 된다.
두 집합에 대한 연산
A | B -> A와 B의 합집합
A & B -> A와 B의 교집합
A & (~B) -> A에서 B를 뺀 차집합
A ^ B -> A와 B 중 하나에만 포함된 원소들의 집합
집합의 크기 구하기
집합 A에서 켜진 bit 수를 구하면 된다. Integer.bitCount(A)를 사용하면 된다.
최소 원소 찾기
집합에 포함된 가장 작은 원소(index)를 찾는 방법.
켜져 있는 bit 중에 가장 오른쪽 비트를 찾는 것이다.
컴퓨터는 2의 보수를 이용하여 음수를 표현하기 때문에 -A를 표현하기 위해서 ~A + 1을 이용한다.
A에서 가장 오른쪽에 켜진 bit의 인덱스를 k라고 한다면, k보다 오른쪽에 있는 모든 bit는 0이다.
따라서 NOT 연산을 적용한 ~A는 k번째 bit는 0이고, 오른쪽의 모든 bit는 1이 된다.
여기서 ~A에 1을 더해주게 되면 k번째보다 오른쪽에 있는 bit는 모두 0이 되고, k번째 bit는 1이 된다.
k번째 bit보다 왼쪽에 있는 bit는 아무런 변화가 없다.
따라서 -A와 A를 AND 시키면 k번째 bit만 켜진 상태로 남게 된다
A & (-A)
최소 원소 지우기
가장 오른쪽에 켜져 있는 bit를 지우고 싶다면 A-1과 AND 시키면 된다.
A에서 1을 빼주게 되면 가장 오른쪽에 있던 bit는 0이 되고 그보다 오른쪽에 있는 모든 bit들이 1이 되기 때문이다.
A & = (A-1)
'PS > 알고리즘' 카테고리의 다른 글
| 최소 신장 트리(Minimum Spanning Tree, MST) (0) | 2023.05.24 |
|---|---|
| 동적계획법(DP) (2) | 2022.12.20 |
| 다익스트라 (0) | 2022.12.18 |
| 너비 우선 탐색(BFS) (1) | 2022.11.14 |
| 깊이 우선 탐색(DFS) (2) | 2022.11.06 |
비트마스크란?
- 비트마스크(BitMask)는 이진수를 사용하는 컴퓨터의 연산 방식을 이용하여,
정수의 이진수 표현을 자료 구조로 쓰는 기법을 말한다.
- 이진수는 0 또는 1을 이용하므로 하나의 비트(bit)가 표현할 수 있는 경우는 두 가지이다.
- 보통 어떤 비트가 1이면 "켜져 있다"라고 말하며, 0이면 "꺼져 있다"라고 말한다.
- 8 bits = 1byte
비트마스크를 사용하면 다음과 같은 이점을 얻을 수 있다.
- 수행시간이 빠르다.
- 코드가 짧다
- 메모리 사용량이 더 적다.
비트 연산자
AND연산 (&)
대응하는 두 비트가 모두 1일 때, 1을 반환
1010 & 1111 = 1010
OR연산(|)
대응하는 두비트가 모두 1 또는 둘 중 하나라도 1이면, 1을 반환
1010 | 1111 = 1111

XOR연산(^)
대응하는 두 비트가 서로 다르면 1을 반환
1010 ^ 1111 = 0101
NOT연산(~)
비트의 값을 반전하여 반환
~1010=0101

예상한 값인 5가 아닌 10에서 2의 보수를 취한 값이 나온다.
시프트연산(>>,<<)
왼쪽 또는 오른쪽으로 비트를 옮긴다.
00001010 << 2 = 101000
00001010 >> 2 = 000010
위의 연산들을 한눈에 비교해보자.


주의점
- 비트 연산자의 우선순위는 비교 연산자보다 낮다.
- ex) a = (10 & 6 == 2)라면 6==2 가먼저 계산되어 0(false)을 반환하고, 이후 10 & 0을 할당
인텔리제이의 경우 에러가 난다.

- 오버플로우(Overflow) 문제이다.
- 오버플로우를 잘 해결하려면 기본값의 타입을 잘 맞추어야 한다


비트마스크의 활용
비트 마스크를 어디에 활용할 수 있을까?
비트마스크는 집합 구현에 매우 효과적이다.
A를 집합이라 두고, 원소는 10개를 갖는다 가정하자.(0~9번째 원소)
쉽게 이해하는 방법은
{A, B, C, D}의 각 원소를 0001, 0010, 0100, 1000이라 생각하면 쉽게 이해될 것이다.
공집합, 모든 원소를 갖는 집합 구하기
공집합은 모든 원소가 없으므로 0을 공집합으로 표현가능하다.
반대로 모든 원소를 갖는 집합은 모든 bit가 1이어야 한다.
1111111111(2) -> (1<<10)-1과 동일하다.
원소 추가 (OR 연산)
A에 특정 원소를 추가하려면 해당하는 bit를 켜야 한다.(1)
A |= (1<<k) 이미 A에 원소에 포함되어 있다면 변화는 없다.
원소 삭제 (AND 연산)
A에 특정 원소를 삭제하려면 해당하는 bit를 꺼야 한다.(0)
A &=~(1<<k)를 사용하여 해당 원소를 0으로 만들 수 있다.
원소의 포함 여부 확인
if(A&(1<<k)) 특정 원소의 포함여부를 알려면, k번째 비트가 켜져 있는지 확인하면 된다.
원소의 토글 (XOR 연산)
A의 집합에서 해당원소가 없으면 추가하고, 있다면 삭제하려면
A^ =(1<<k)를 해주면 된다.
두 집합에 대한 연산
A | B -> A와 B의 합집합
A & B -> A와 B의 교집합
A & (~B) -> A에서 B를 뺀 차집합
A ^ B -> A와 B 중 하나에만 포함된 원소들의 집합
집합의 크기 구하기
집합 A에서 켜진 bit 수를 구하면 된다. Integer.bitCount(A)를 사용하면 된다.
최소 원소 찾기
집합에 포함된 가장 작은 원소(index)를 찾는 방법.
켜져 있는 bit 중에 가장 오른쪽 비트를 찾는 것이다.
컴퓨터는 2의 보수를 이용하여 음수를 표현하기 때문에 -A를 표현하기 위해서 ~A + 1을 이용한다.
A에서 가장 오른쪽에 켜진 bit의 인덱스를 k라고 한다면, k보다 오른쪽에 있는 모든 bit는 0이다.
따라서 NOT 연산을 적용한 ~A는 k번째 bit는 0이고, 오른쪽의 모든 bit는 1이 된다.
여기서 ~A에 1을 더해주게 되면 k번째보다 오른쪽에 있는 bit는 모두 0이 되고, k번째 bit는 1이 된다.
k번째 bit보다 왼쪽에 있는 bit는 아무런 변화가 없다.
따라서 -A와 A를 AND 시키면 k번째 bit만 켜진 상태로 남게 된다
A & (-A)
최소 원소 지우기
가장 오른쪽에 켜져 있는 bit를 지우고 싶다면 A-1과 AND 시키면 된다.
A에서 1을 빼주게 되면 가장 오른쪽에 있던 bit는 0이 되고 그보다 오른쪽에 있는 모든 bit들이 1이 되기 때문이다.
A & = (A-1)
'PS > 알고리즘' 카테고리의 다른 글
| 최소 신장 트리(Minimum Spanning Tree, MST) (0) | 2023.05.24 |
|---|---|
| 동적계획법(DP) (2) | 2022.12.20 |
| 다익스트라 (0) | 2022.12.18 |
| 너비 우선 탐색(BFS) (1) | 2022.11.14 |
| 깊이 우선 탐색(DFS) (2) | 2022.11.06 |
